r:=t->cos(t)+1 //Kardioide
![]()
Kardioide und ihr karstesisches Gegenstück
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Mrz. 06 (Version 3 ex.) Update 20.08.07
www.mathematik-verstehen.de https://mathe.web.leuphana.de
Berührt die Kardioide ihr kartesisches Gegenstück?
r:=t->cos(t)+1 //Kardioide
![]()
kardioide:=plot::Polar([r(t),t],t=0..2*PI
,LineColor=RGB::Red, LineWidth=1):
kardioKartes:=plot::Function2d(r(t),t=0..2*PI
,LineColor=RGB::Green, LineWidth=1):
kardioKartesInv:=plot::Function2d(1/r(t),t=0..2*PI,
ViewingBoxYMax=2):
pkt:=plot::Point2d([PI/2,1],Color=RGB::Black
,PointSize=3,PointStyle=Stars):
plot(kardioide,kardioKartes,pkt,kardioKartesInv)
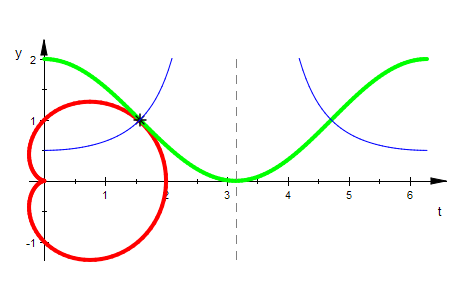
Sehen wir uns das genauer an:
Man kann auch die Graphik anklicken und das Zoomwerkzeug verwenden.
plot(kardioide,kardioKartes,pkt, ViewingBox=[1.5..1.8,0.8..1.1])
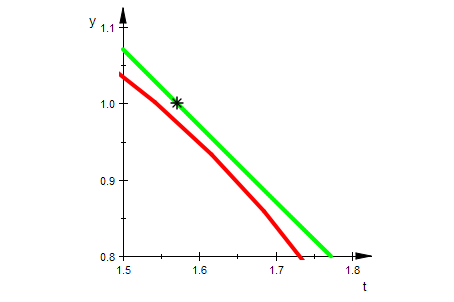
Damit ist alles klar.
Vermutung war: kartesisch (Pi/2,1) könnte der Schnittpunkt sein
Bestimmung des Polarwinkels dieses Punktes
arctan(2/PI); // tan(ts)=y/x=1/(PI/2)
ts:=float(%);
rs:=sqrt((4+PI^2)/4);//aus Pythagoras
float(rs); //Polarradius dieses Punktes
rk:=cos(ts)+1;//Polarradius dazu aus Kardioide
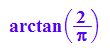
![]()
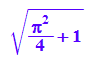
![]()
![]()
Das ist aber kein gemeinsamer Polarradius.
Übrigens: Zeichnen ist hier stärker als Rechnen!
Denn so wird klar, dass es auch keine anderen als den vermuteten
Schnittpunkt gibt.