Kosinus-Rosette mit Konchoide
und die Doppel-Ei-Linie
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Mrz. 06 (Version 3 ex.) Update 20.08.07
www.mathematik-verstehen.de https://mathe.web.leuphana.de
Rosette, zu der es unten eine Konchoide gibt
hl:=1: //Leinenlänge
r:=t->cos(2*t);
rosette:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
pkt:=plotPoint2d([r(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
leine:=plot::Line2d([(r(t)+hl)*cos(t),(r(t)+hl)*sin(t)],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
rosettekart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
plot(rosette,radiusbetrag2,radius2,rosettekart,radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth);
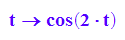
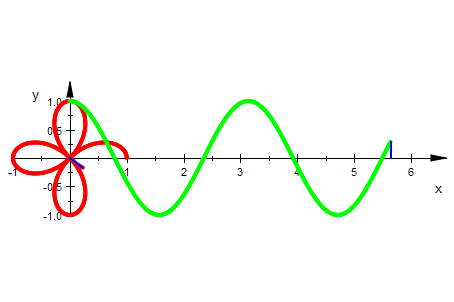

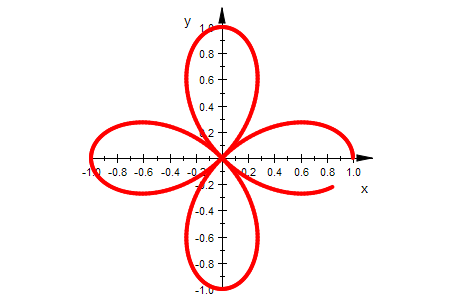
plot(rosette);

Konchoide der Rosette
Spezielle Leinelänge hl, def. oben
r:=t->cos(2*t)+hl;
rosetteconch:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,1], Mesh=400):
rosetteconchkart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radiusconch:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetragconch:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordiconch:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
plot(rosette,rosetteconch,leine,
AnimationStyle=BackAndForth);
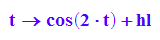
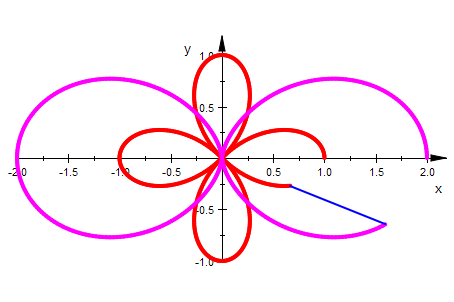
Die Konchoide der Rosette ist die (eine) Doppel-Ei-Linie
Übliche Formel der Doppel-Ei-Linie, Größe angepasst
r:=t->2*cos(t)^2;
doppei:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1, LineColor=RGB::Red, Mesh=400):
doppeid:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1, LineColor=RGB::Red, Mesh=400,LineStyle=Dashed):
doppeikart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radiusdoppei:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetragdoppei:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineWidth=0.5,LineColor=[0,1,0]):
radiusordidoppei:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
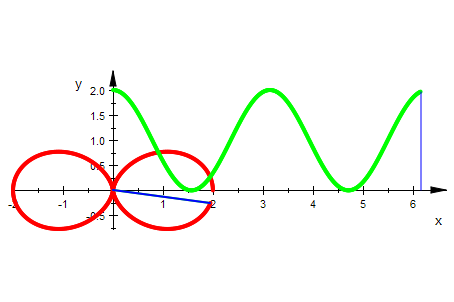
plot(doppei,radiusbetragdoppei,radiusdoppei,doppeikart,radiusordidoppei,
AnimationStyle=BackAndForth);
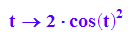

plot(rosetteconch,doppeid)
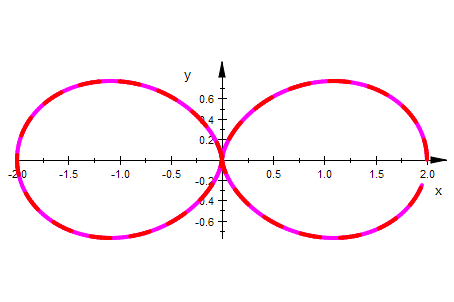

Die beiden Doppel-Ei-linien scheinen übereinzustimmen.
Rechnerieche Prüfung:
dei1:=2*cos(t)^2
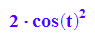
dei2:=expand(cos(2*t)+1)
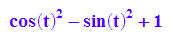
simplify(dei1-dei2)
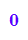
Also ist für Leinenlänge =Blattlänge die Konchoide
der Cos-Rosette die übliche Doppel-Ei-Linie
![]()





