r:=t->cos(2*t);
rosette:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
plot(rosette);
![]()
Bogenlänge und Fläche der Rosette
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4 (es ex. in Version 3), Mrz. 06 Update 20.08.07
www.mathematik-verstehen.de https://mathe.web.leuphana.de
Es existiert noch die alte Version in MuPAD 2.5 (zur Not) von Mai 04
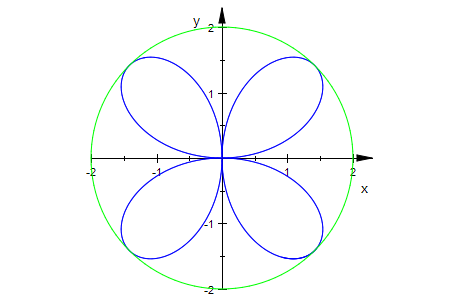
Kosinus-Rosette (Sinus-Rosette unten)
r:=t->cos(2*t);
rosette:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
plot(rosette);
![]()


pkt:=plotPoint2d([r(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
rosettekart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
plot(rosette,radiusbetrag2,radius2,rosettekart,radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth);
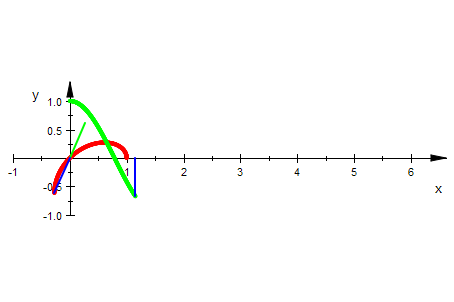

Weiteres zur polar-kartesischen Darstellung auf Extraseite
####################################
Implizite Gleichung der Rosette (aus dem Bereich Kurven->Terme)
oder aus der einfachen Polargleichung (s.u.) leicht herleitbar.
rosettegl:=(x^2+y^2)^3=c^2*x^2*y^2
![]()
c:=4:rosimp:=plot::Implicit2d(rosettegl,x=-2..2,y=-2..2):
kreis:=plot::Polar([c/2,phi],phi=0..2*PI, LineColor=RGB::Green):
plot(kreis,rosimp,Scaling=Constrained, LineWidth=1);delete(c):
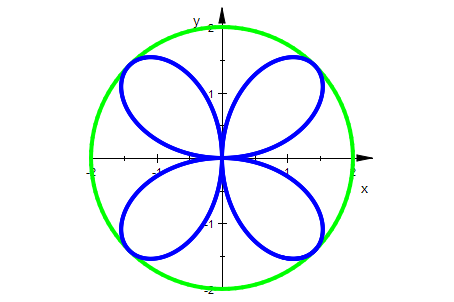

c=Durchmesser des Umkreises, unten a:=Radius=c/2
Man kann das von Hand nicht nach y auflösen, darum ist die Darstellung in Polarkoordinaten besser.
solve(rosette,y)
![]()
solve((xx+yyy)^3=c^2*xx*yy,yy)
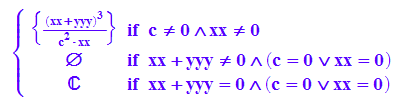
Wie man es auch vesucht, es kommt nichts heraus.
Arbeit in Polarkoordinaten
Polargleichung der Rosette (experimenrtell gefunden oder aus dem Bereich Kurven->Terme)
oder aus der impliziten Gleichung der Rosettengleichung (s.o.) leicht herleitbar.
r:=phi->(a*sin(2*phi))
![]()
a:=2:
plotfunc2d(r(phi))
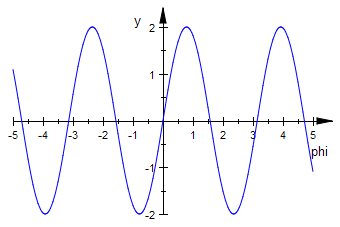
Das ist also eine einfache Sinuskurve, Amplitude 2, Kreisfrequenz 2.
rg:=plot::Polar([r(phi),phi],phi=0..2*PI):plot(rg)
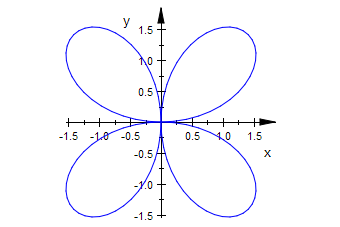
delete(a):
diff(r(phi),phi)
![]()
Term für die kleine Bogenlängenänderung ds=d l
sqrt(r(phi)^2+diff(r(phi),phi)^2)
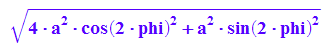
Berechnung der Bogenlänge
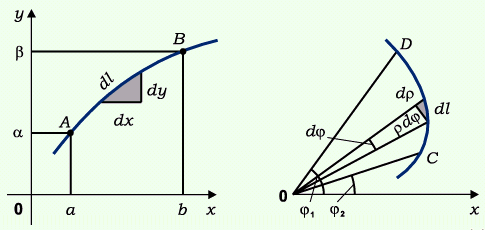
int(sqrt(r(phi)^2+4*a^2*cos(2*phi)^2), phi)
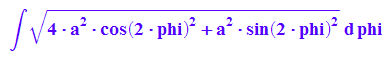
Das Integral ist zu schwierig zu berechnen, es gibt keine Stammfunktion.
Einstzen von a=2 bringt auch nichts.
Das bestimmte Integral funktioniert daher auch nicht exakt.
int(sqrt(r(phi)^2+16*cos(2*phi)^2), phi=0..PI/2)
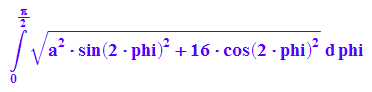
Numerische Integration hilft da weiter (mit a=2):
bl:=numeric::int(sqrt((2*sin(phi))^2+16*cos(2*phi)^2), phi=0..PI/2)
![]()
Das ist also die Bogenlänge eines Blattes.
Die ganze Rosette:
4*bl
![]()
Sie ist etwa 6 PI lang, der Kreis hat einen Umfang von 2 PI
Fläche der Rosette
Die folgende Formel macht man sich klar, indem man das kleine Tortenstück betrachtet,
das von der kleinen Winkeländerung d phi und dem Radius r gebildet wird,
Dann wird über alle Tortenstückchen summiert, das heißt es wird integriert.
int(1/2*r(phi)^2, phi)
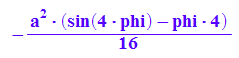
delete(a):
frosette:=1/2*int(r(phi)^2, phi=0..PI/2)
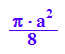
subs(%, a=2)
![]()
Das ist die Fläche eines Blattes bei Radius 2.
Die Fläche der Rosette bei Radius a ist also
4*frosette
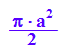
Sie nimmt also genau die Hälfte des Umkreises ein.
plot(rosimp,kreis,Scaling=Constrained);