sp:=plot::Polar([ln(t),t],t=0.001..50, Mesh=500):plot(sp)
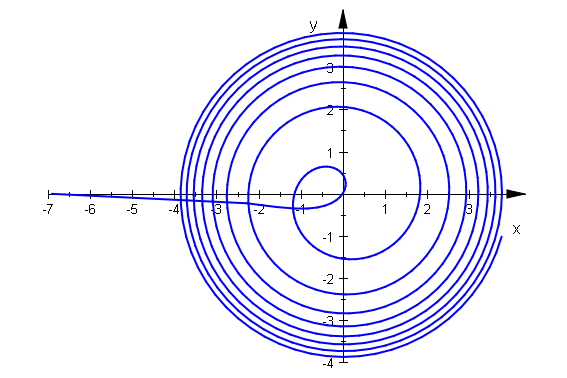
Logarithmische Spirale
Prof. Dr. Dörte Haftendorn, Juni 09 Update 19.06.09
www.mathematik-verstehen.de https://mathe.web.leuphana.de
##################################################################
sp:=plot::Polar([ln(t),t],t=0.001..50, Mesh=500):plot(sp)

Schnitte mit der x-Achse: x=0, x=![]()
ln(k*PI)
![]()
Der Ursprung wird erreicht für t=1
float(tan(1)); float(arctan(%)/PI*180),"Grad"
![]()
![]()
Dies ist der Steigungswinkel der Schlaufe im Ursprung.
Zugehörige kartesische Darstellung
plotfunc2d(ln(t), ln(2*k*PI)$ k=1..10,ln(2*9*PI),t=0..20*PI, LegendVisible=FALSE)
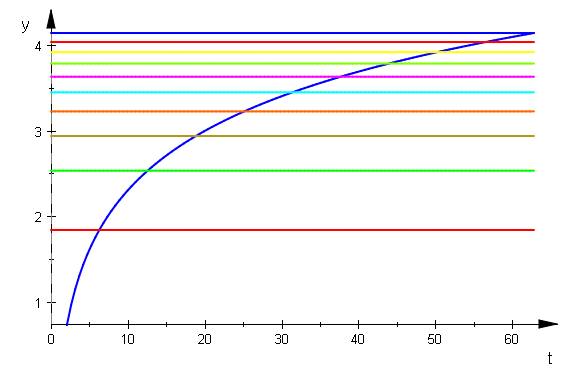
Hier sieht man, dass sie nach außen zu immer enger wird.
float(ln(k*PI/4+2*PI)-ln(k*PI/4)) $ k=1..6
![]()
Darstellung der Abstände
plotfunc2d(ln(t+2*PI)-ln(t),t=0..300, Axes=Origin, ViewingBoxYRange=0..3)
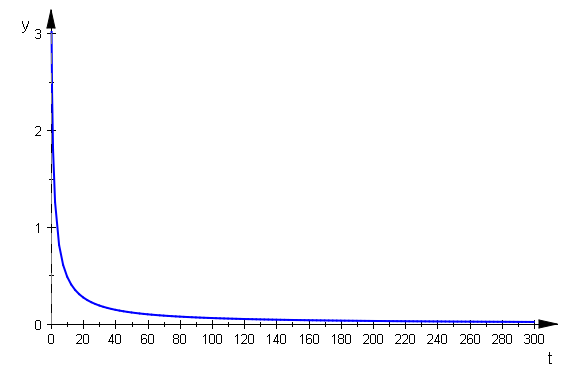
Die Breite der Spiralenringe geht gegen Null. Die Breite der gesamten logarithmischen Spirale ist aber nicht beschränkt.
##############################################
Betrachtung der Fläche
iterm:=x->1/2*int(ln(t)^2, t=1..x): iterm(x)
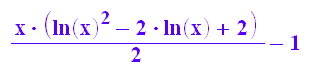
1/2*int(ln(t)^2, t=1..PI/2);float(%)
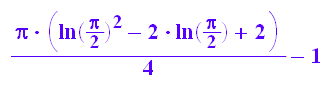
![]()
Dies ist die winzige Fläche im 1. Quadranten
#####################################
Berechnungen für die Schlaufe:
Schnitt mit sich
solve(-ln(t)=ln(t+PI),t);
lo:=solve(0=ln((t+PI)*t),t);float(%)
![]()
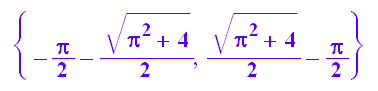
![]()
Der zweite Wert erzeugt einen negativen Radius und ist der Parameterwert
der Spitze.
float(arctan(lo[2])/PI*180);float(%+180);
![]()
![]()
float(1/2*int(ln(t)^2,t=lo[2]..lo[2]+PI))
![]()
Dies ist der Flächeninhalt der kleinen Schlaufe
plotfunc2d(1/2*ln(lo[2])^2,1/2*ln(t)^2,t=lo[2]..lo[2]+PI,
LegendVisible=FALSE)
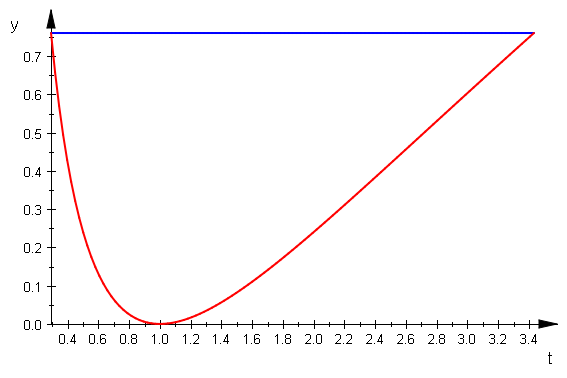
Hier sieht man nochmals, dass der Winkel richtig berechnet ist,
bei dem die Schlaufe ihre Spritze hat.
Steigungen an dieser Spitze:
r:=t->ln(t)
![]()
steig:=t->(r'(t)*sin(t)+r(t)*cos(t))/(r'(t)*cos(t)-r(t)*sin(t))
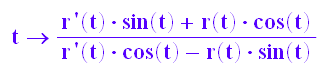
plotfunc2d(steig(t),t=0.01..6)
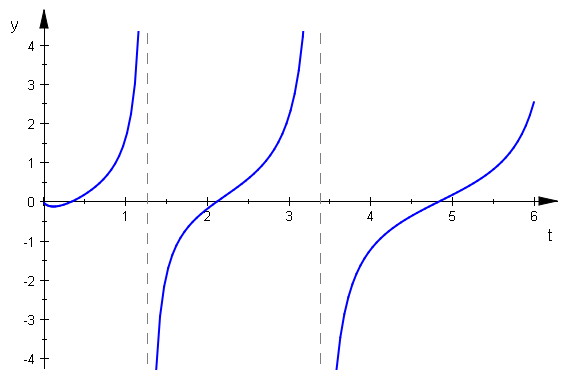
Die einzige Wendestelle ist als Extremstelle gut zu sehen.
Nenner und Zähler extra:
denom(steig(t)), numer(steig(t))
![]()
Polarwinkel, bei denen waagerechte Tangenten vorliegen.
numeric::solve(numer(steig(t))=0,t=1);
numeric::solve(numer(steig(t))=0,t=2);
numeric::solve(numer(steig(t))=0,t=5);
![]()
![]()
![]()
Polarwinkel, bei denen senkrechte Tangenten vorliegen.
numeric::solve(denom(steig(t))=0,t=1);
numeric::solve(denom(steig(t))=0,t=3);
numeric::solve(denom(steig(t))=0,t=6);
![]()
![]()
![]()
Spitzenwinkel der Schlaufe:
st1:=float(steig(lo[2]));arctan(st1);w1:= float(%/PI*180);
st2:=float(steig(lo[2]+PI));arctan(st2);w2:= float(%/PI*180);
w1-w2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Der Winkel in der Spitze der Schlaufe ist 83,52°.
sps:=plot::Polar([ln(t),t],t=lo[2]..lo[2]+PI, Mesh=500):plot(sps)
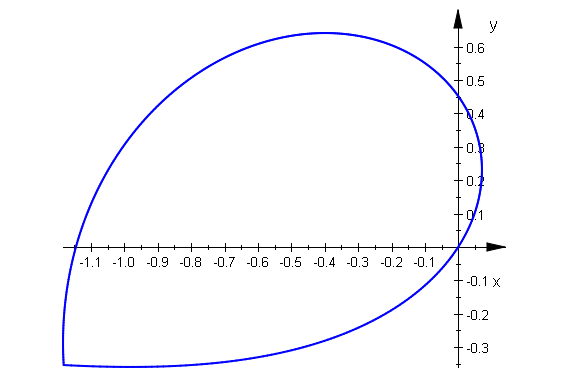
Kartesische Kordinaten der Spitze der Schlaufe:
xs:=float(r(lo[2])*cos(lo[2]));
ys:=float(r(lo[2])*sin(lo[2]));
![]()
![]()