sp:=plot::Polar([sqrt(t),t],t=0..20*PI, Mesh=500):plot(sp)
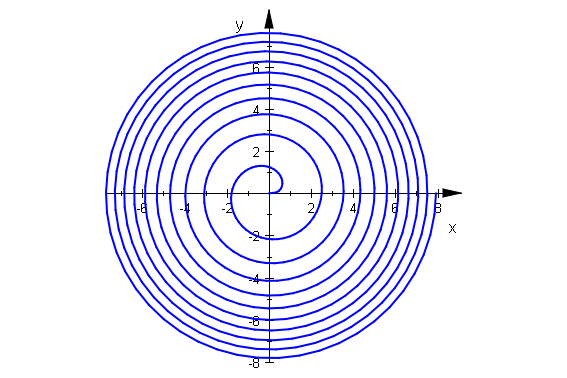
Wurzelspirale
Prof. Dr. Dörte Haftendorn, Juni 09 Update 19.06.09
www.mathematik-verstehen.de https://mathe.web.leuphana.de
##################################################################
sp:=plot::Polar([sqrt(t),t],t=0..20*PI, Mesh=500):plot(sp)

Zugehörige Kartsesische Darstellung
plotfunc2d(sqrt(t), sqrt(2*k*PI)$ k=1..10,sqrt(2*9*PI),t=0..20*PI, LegendVisible=FALSE)
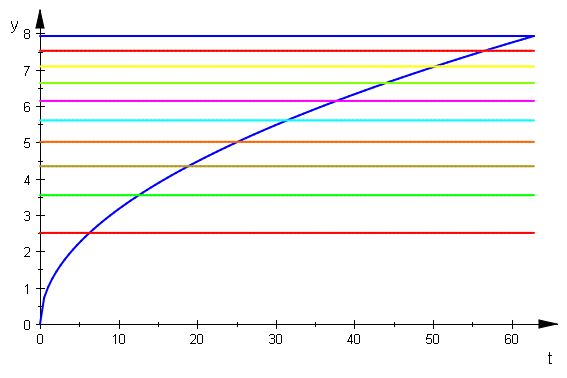
Hier sieht man, dass sie nach außen zu immer enger wird.
Darstellung der Abstände
plotfunc2d(sqrt(t+2*PI)-sqrt(t),t=0..300, Axes=Origin, ViewingBoxYRange=0..3)
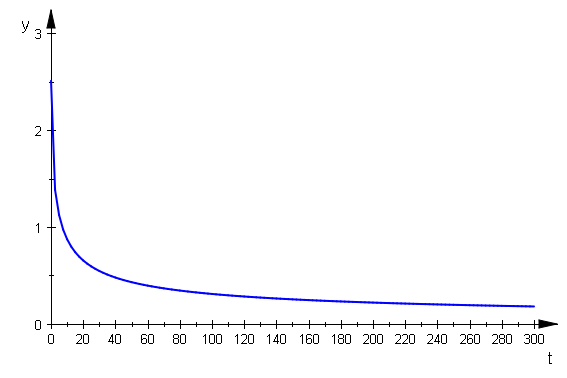
Die Breite der Spiralenringe geht gegen Null. Die Breite der gesamten Wurzelspirale ist aber nicht beschränkt.
##############################
r:=t->sqrt(t);
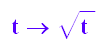
steig:=t->(r'(t)*sin(t)+r(t)*cos(t))/(r'(t)*cos(t)-r(t)*sin(t))
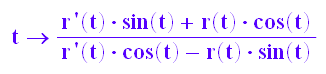
plotfunc2d(steig(t),t=0..10)
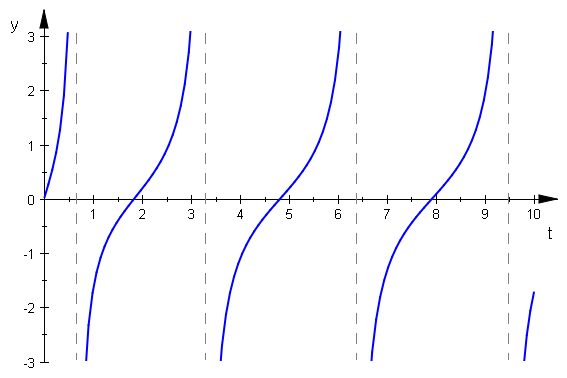
Die einzige Wendestelle ist als Extremstelle gut zu sehen.
Nenner und Zähler extra:
denom(steig(t)), numer(steig(t))
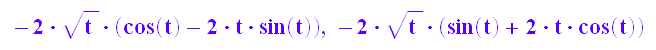
Polarwinkel, bei denen waagerechte Tangenten vorliegen.
numeric::solve(numer(steig(t))=0,t=0);
numeric::solve(numer(steig(t))=0,t=2);
numeric::solve(numer(steig(t))=0,t=5);
![]()
![]()
![]()
Polarwinkel, bei denen senkrechte Tangenten vorliegen.
numeric::solve(denom(steig(t))=0,t=1);
numeric::solve(denom(steig(t))=0,t=3);
numeric::solve(denom(steig(t))=0,t=6);
![]()
![]()
![]()
Steigungen in den Nullstellen
simplify(steig(k*PI)) $ k=1..10;
![]()
Steigungen in den Durchgängen durch die y-Achse
simplify(steig((2*k+1)/2*PI)) $ k=1..10;
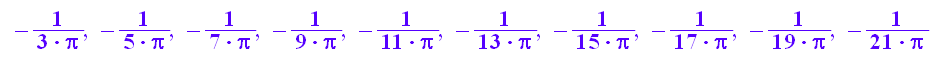
Rechts und links werden die Nulldurchgänge immer steiler,
oben und unten immer flacher.
##############################################
Betrachtung der Fläche
iterm:=x->1/2*int(t, t=0..2*k*PI): iterm(x)
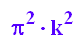
Bei der polaren Flächenbestimmung wird bei jeder Runde das Innere ganz überstrichen. Daher ist bei k Runden nur der letzte Ring einmal in der mit dem Integral berechneten Fläche, der vorige doppelt , davor dreifach und so weiter.
t1:=0:iterm(2*k*PI) $ k=1..4
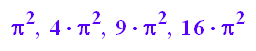
sc1:=plot::Scene2d(plot::Polar([sqrt(t),t],t=0..2*PI, Mesh=500)):
sc2:=plot::Scene2d(plot::Polar([sqrt(t),t],t=0..4*PI, Mesh=500)):
sc3:=plot::Scene2d(plot::Polar([sqrt(t),t],t=4*PI..8*PI, Mesh=500)):
sc4:=plot::Scene2d(plot::Polar([sqrt(t),t],t=6*PI..10*PI, Mesh=500)):
plot(sc1,sc2,sc3,sc4)
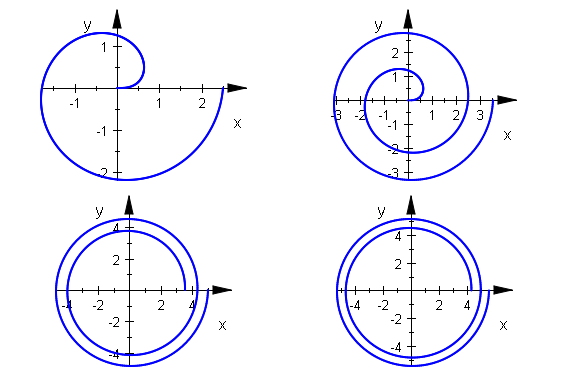
Die 1. Fläche bis 3. Flächen der Ringe sind
PI^2,4*PI^2-2*PI^2,9*PI^2-2*(4*PI^2-2*PI^2)-3*PI^2
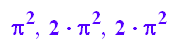
Die 4. Fläche
PI^2*(16-2*2-3*2-4*1)
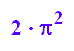
Die k-te Fläche
PI^2*(k^2-2*sum(k,k=2..(k-1))-k*1);
expand(%)
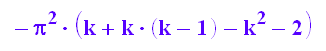
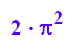
Erstaunliches Ergebnis: alle die Spiralenringe haben den Flächeninhalt 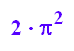
###########################################################
Betrachtung von Kreisringen, die auch durch die rechten Achsenschnittpunkte
gehen.
PI*2*(k+1)*PI-PI*2*k*PI;
expand(%)
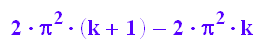
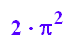
Auch diese Ringe haben in jeder Größe den Flächeninhalt 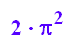 .
.
kr1:=plot::Circle2d(sqrt(2*k*PI)|k=1,[0,0], LineColor=[1,0,0]):
kr2:=plot::Circle2d(sqrt(2*k*PI)|k=2,[0,0], LineColor=[1,0,0]):
sc1:=plot::Scene2d(kr1,kr2,plot::Polar([sqrt(t),t],t=2*PI..6*PI, Mesh=500)):
kr3:=plot::Circle2d(sqrt(2*k*PI)|k=2,[0,0], LineColor=[1,0,0]):
kr4:=plot::Circle2d(sqrt(2*k*PI)|k=3,[0,0], LineColor=[1,0,0]):
sc2:=plot::Scene2d(kr3,kr4,plot::Polar([sqrt(t),t],t=4*PI..8*PI, Mesh=500)):
plot(sc1,sc2)
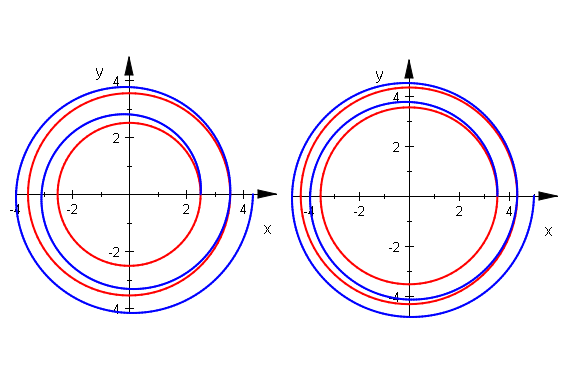
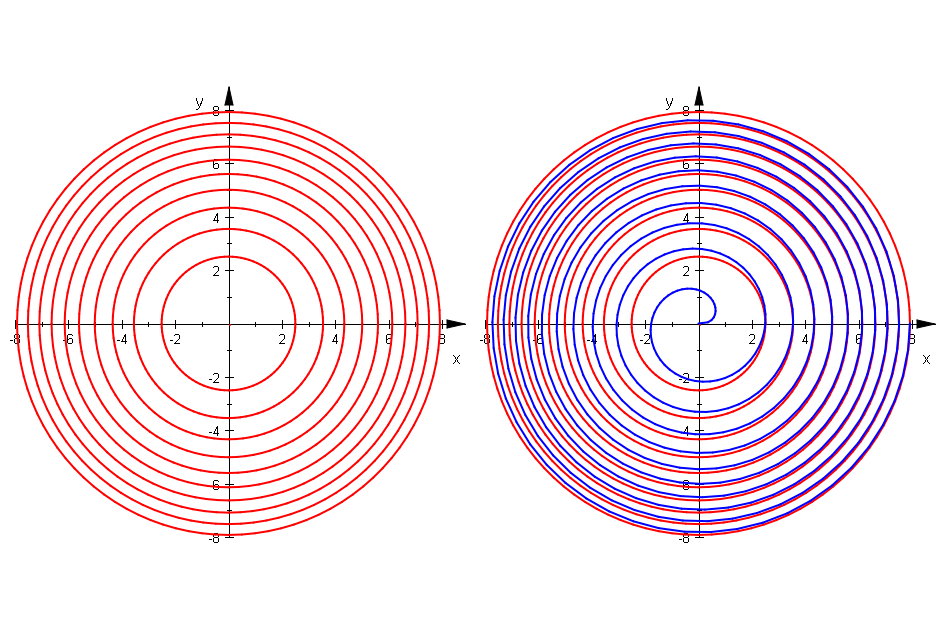
kreise:=(plot::Circle2d(sqrt(2*(k-1)*PI), LineColor=[1,0,0]) $ k=1..11):
sc1:=plot::Scene2d(kreise):
sc2:=plot::Scene2d(kreise,sp):
plot(sc1,sc2)