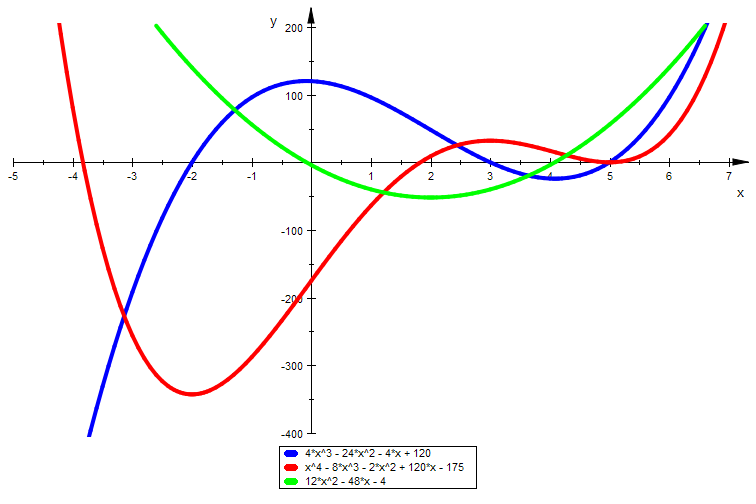
Polynom aus einem Analysis-Erklärungsbuch
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4, Mai 07 Update Mai 07
https://mathe.web.leuphana.de www. mathematik-verstehen.de
###############################################################
Diese Seite ist ein Appell, Mathematik so!!!! nicht!!!! zu betreiben.
Es lässt sich hier allerlei für einen anderen Mathematikunterricht lernen.
Zunächst eine Darstellung, wie sie die GTR, die meist ein Standardfenster haben, liefern:
f:=x->x^4-8*x^3-2*x^2+120*x+7
![]()
plotfunc2d(f(x),x=-5..5,ViewingBoxYRange=-5..5)
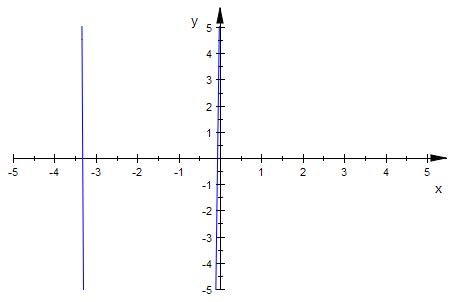
Da ist nicht viel zu sehen.
Der Versuch, evt. x=7 als ganzzahlige Nullstelle zu finden füht auf:
f(7)
![]()
plotfunc2d(f(x),x=-5..7)
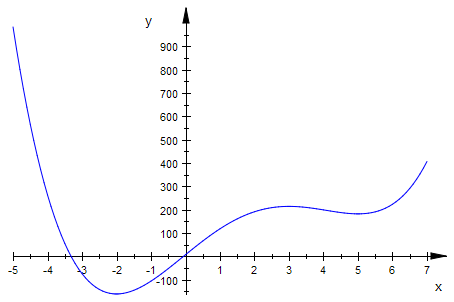
Damit ist aber nun auch in einem qualtitativen Sinn alles klar.
Ersichtlich sind es drei Extrema, die Stellen seien x1, x2, x3.
Da f ' als Polynom 3. Grades ja nicht mehr als 3 Nullstellen haben kann,
kann also außerhalb des gezeigten Fensters nichts Wesenliches mehr passieren.
Es mathematischer Unsinn, bei so einem Polynomgraphen noch zu zweifeln.
Interessant sind allenfalls noch die genauen Werte der Extremstellen.
Streng monoton fallend für x<x1 und x2<x<x3
Streng monoton wachsend für x1<x<x2 und x3<x
Angeregt durch den obigen Text, erwartet man nun glatte Nullstellen der Ableitung
f'(x)
![]()
solve(f'(x)=0,x)
![]()
Tatsächlich, drei einfache Nullstellen von f', wie es oben erwähnt ist.
factor(f'(x))
![]()
Damit ist aber nun auch gleich alles klar.
f ist streng monoton fallend für x<-2 und 3<x<5
f ist Steng monoton wachsend für -2<x<3 und 5<x
Aus meine Sicht ist so eine Monotoniefrage sowieso nicht so toll.
Diese Vorzeichenbetrachtung hat höchsten ihren Sinn, wenn man f' als gegeben voraussetzt, und dann durch
Felderabstreichen zu einem qualitativen Graphen von f ' kommt und dann qualitativ
und auch durch Aufleiten f bestimmt.
######################################################
Nun erzeuge ich aus dieser Grundidee eine Funktion, die sich ohne CAS bearbeiten lässt.
Dazu lege ich das rechte Minimum auf die x-Achse
f(5)
![]()
g:=x-->f(x)-182
![]()
plotfunc2d(g(x),x=-5..7)
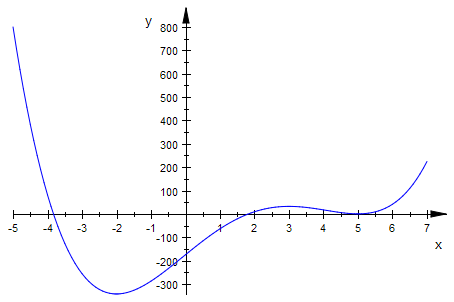
Hier können nun alle Nullstellen von Hand gefunden werden, z.B. mit dem erweiterten
Hornerschema und der übrigbleibenden quadratischen Gleichung.
solve(g(x)=0,x)
![]()
Sicher hat g nun dieselbe Ableitung wie f.
g'(x)
![]()
solve(g'(x)=0,x)
![]()
factor(g'(x))
![]()
g''(x)
![]()
factor(g''(x))
![]()
solve(g''(x)=0,x)
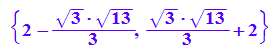
Hier sind auch gleich noch die bei Polynomen zu drei Extrema gehörigen zwei Wendestellen.
plotfunc2d(g'(x),g(x),g''(x),x=-5..7, ViewingBoxYRange=-400..200, LineWidth=1)