Weihnachtsbaum-Polynome
Ein Geschenk meines guten Freundes
Prof. Dr. Dieter Riebesehl, Universität Lüneburg
Prof. Dr. Dörte Haftendorn Silvester 2004
Was sind "schöne Polynome"?
das sind solche die reduzibel sind
- p1:=x->x^7+2*x^3+1;
factor(p1(x))
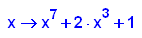
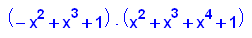
- p2:=x->x^7+2*x^4+1;
factor(p2(x))
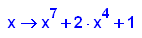
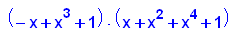
- p3:=x->x^10+x^2+1;
factor(p3(x))
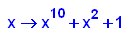
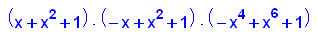
- p4:=x->x^10+x^2+2;
factor(p4(x))
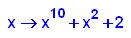
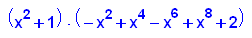
- p5:=x->x^5+20*x+32;
factor(p5(x))
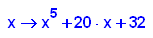
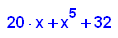
- p5b:=x->x^5+31*x+32;
factor(p5b(x))
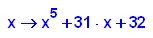
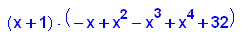
- p6:=x->x^4+sqrt(3)*x+2;
factor(p6(x))
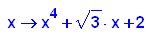
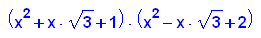
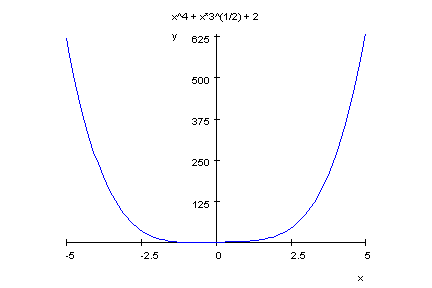

- plotfunc2d(p6(x),sqrt(3)*x+2,x=-2..2,y=-1..6)
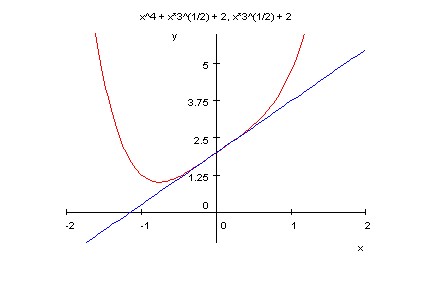

- p7:=x->x^10+11*x^2+12;
factor(p7(x))
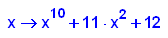
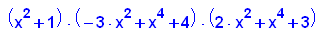
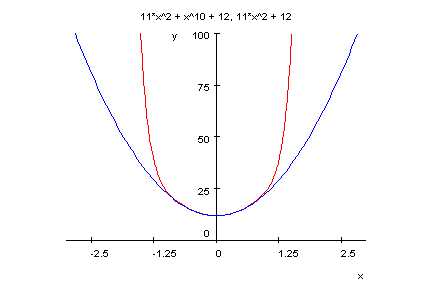
- plotfunc2d(p7(x),11*x^2+12,x=-3..3,y=-1..100)

- p8:=x->4*x^6+2*x+1;
factor(p8(x))
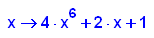
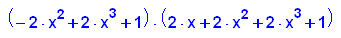
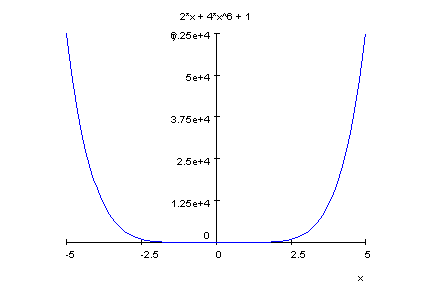

- plotfunc2d(p8(x),x=-1..1,y=-0.1..10)
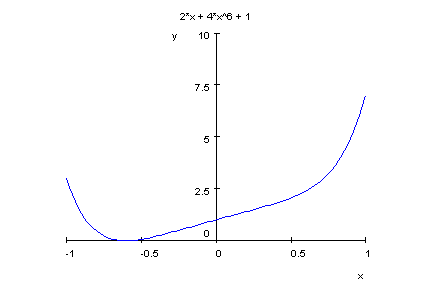

- plotfunc2d(p8(x),x=-0.8..-0.5,y=-0.1..0.1)
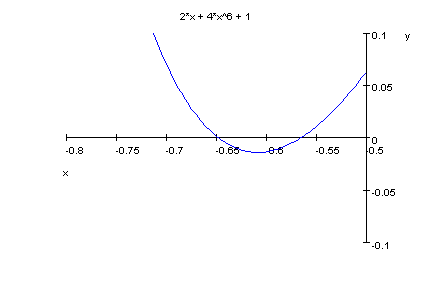

- p9:=x->x^10+25*x^2+26;
factor(p9(x));
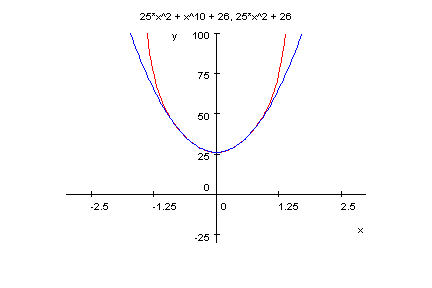
plotfunc2d(p9(x),25*x^2+26,x=-3..3,y=-30..100)
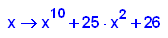
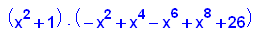

- p9b:=x->x^10+25*x^2-26;
factor(p9b(x));
plotfunc2d(p9b(x),25*x^2-26,x=-3..3,y=-30..100)
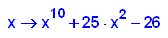
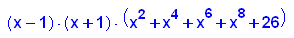
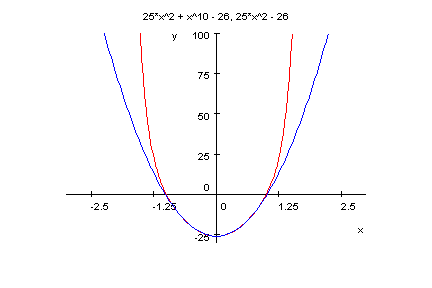

- p9c:=x->x^10+25*x-26;
factor(p9c(x));
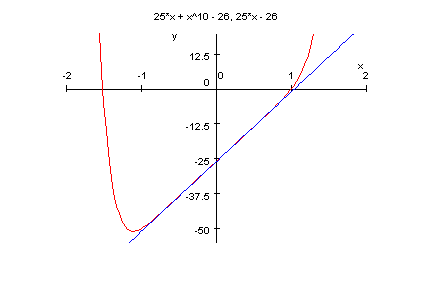
plotfunc2d(p9c(x),25*x-26,x=-2..2,y=-55..20)
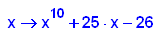
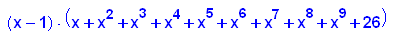

- p10:=x->x^10+sqrt(2)*x+1;
factor(p10(x));
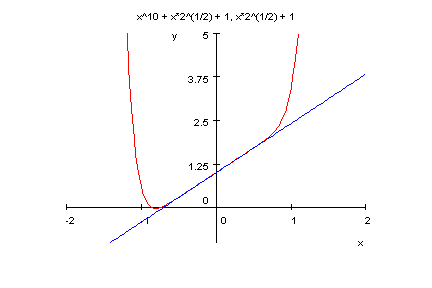
plotfunc2d(p10(x),sqrt(2)*x+1,x=-2..2,y=-1..5)
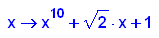
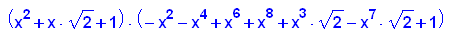

- solve(x^2+sqrt(2)*x+1,x)// der kleine Faktor hat keine Nst
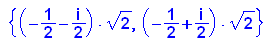
- nst:=numeric::solve(p10(x)=0)
{[x = - 0.1109842386 + 1.049035386 I],
[x = - 0.1109842386 - 1.049035386 I],
[x = - 0.7071067812 + 0.7071067812 I],
[x = - 0.7071067812 - 0.7071067812 I],
[x = 0.5817264373 + 0.9143742811 I],
[x = 0.5817264374 - 0.9143742811 I], [x = -0.7437103212],
[x = -0.8553738539], [x = 1.03590667 + 0.3600763067 I],
[x = 1.03590667 - 0.3600763067 I]}

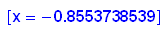
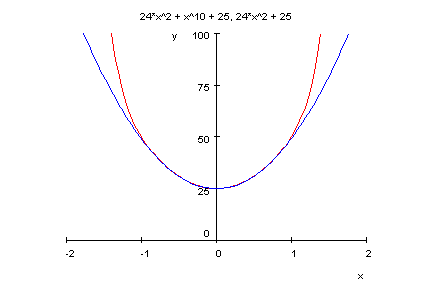
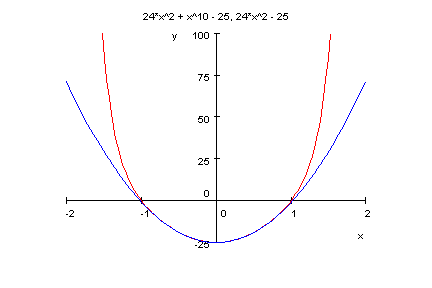
- p11:=x->x^10+24*x^2+25;
factor(p11(x));
plotfunc2d(p11(x),24*x^2+25,x=-2..2,y=-1..100)
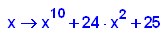
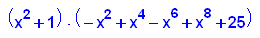

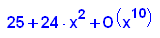
- p11b:=x->x^10+24*x^2-25;
factor(p11b(x));
plotfunc2d(p11b(x),24*x^2-25,x=-2..2,y=-25..100)
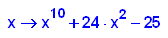
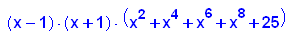

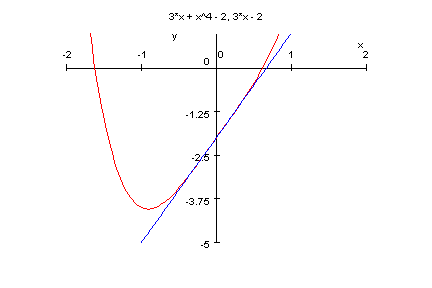
- p12:=x->x^4+3*x-2;
factor(p12(x));
plotfunc2d(p12(x),3*x-2,x=-2..2,y=-5..1)
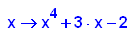
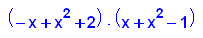

Ganz erstaunliche Sachen kommen da bei der Zerlegung:
- factor(x^(2*k)+3*x+2)$k=1..40:
- factor(x^(2*k+1)+3*x+2)$k=1..40:
Alle mit geradem Grad bieten (x+1) als Faktor (klar), aber
dann fast alle unzerlegbar mit alternierenden Vorzeichen und ausschließlich
Faktoren 1 alle Potenzen. Hinten steht +2 (klar):
Erstaunlicherweise habe ich bis x^80 nur ein Polynom gefunden,
das weiter zerlegbar ist, und zwar das vom 8. Grad.
Alle mit ungeradem Grad sind unzerlegbar, bis x^81
Bei Variation der 3 und der 2 fand ich auch nur unzerlegbare
(allerdings habe ich nicht systematisch gesucht.)
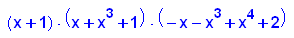
- expand((x+x^3+1)*(-x-x^3+x^4+2))
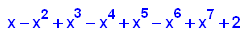
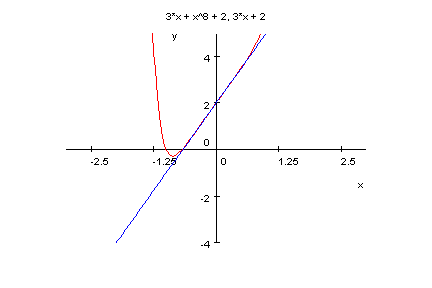
- plotfunc2d(x^(8)+3*x+2,3*x+2,x=-3..3,y=-4..5)

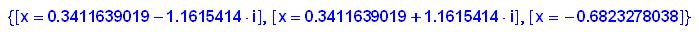
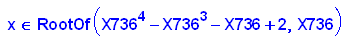
- nst:=numeric::solve(x^8+3*x+2)


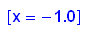
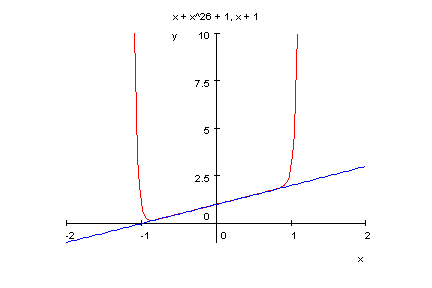
- p13:=x->x^26+x+1;
factor(p13(x));
plotfunc2d(p13(x),x+1,x=-2..2,y=-1..10)
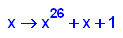
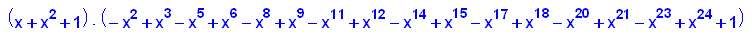

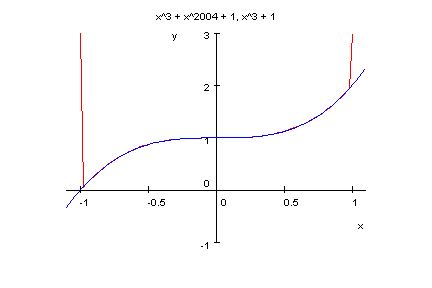
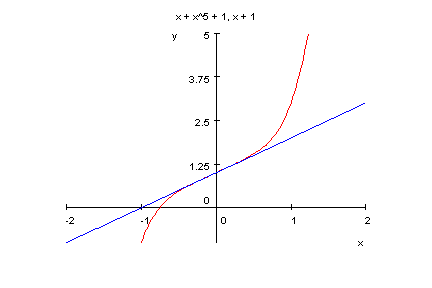
- p14:=x->x^2004+x^3+1;
plotfunc2d(p14(x),x^3+1,x=-1.1..1.1,y=-1..3)
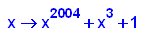

Error: Computation aborted;
during evaluation of 'faclib::univ_mod_gcd'
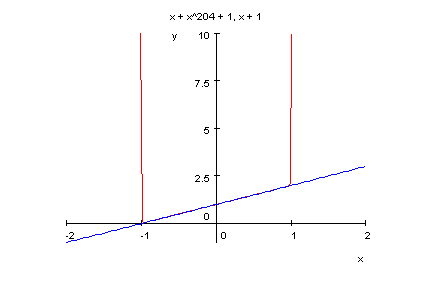
- p14b:=x->x^204+x+1;
factor(p14b(x));
plotfunc2d(p14b(x),x+1,x=-2..2,y=-1..10)
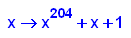
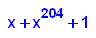

- p15:=x->x^7+7*x+10;
factor(p15(x));
plotfunc2d(p15(x),7*x+10,x=-2..2,y=-1..20)
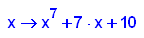
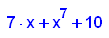
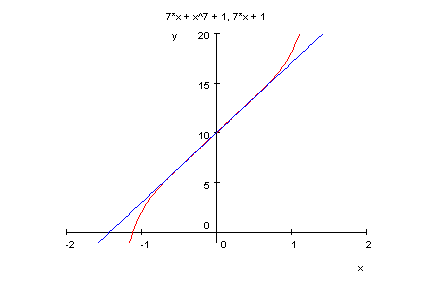

- p16:=x->x^7+x^2+1;
factor(p16(x));
plotfunc2d(p16(x),x^2+1,x=-2..2,y=-1..20)
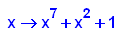
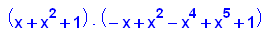
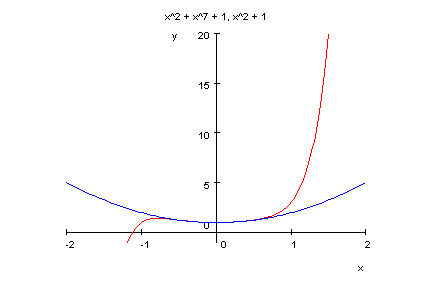

- p17:=x->x^25+x^2+1;
factor(p17(x));
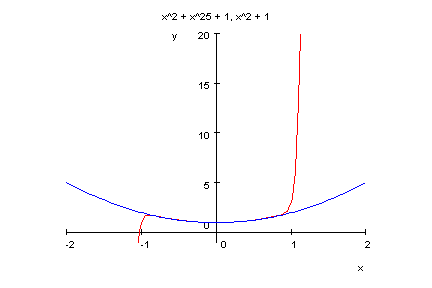
plotfunc2d(p17(x),x^2+1,x=-2..2,y=-1..20)
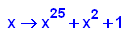
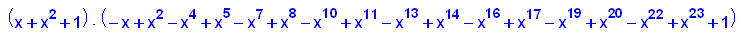

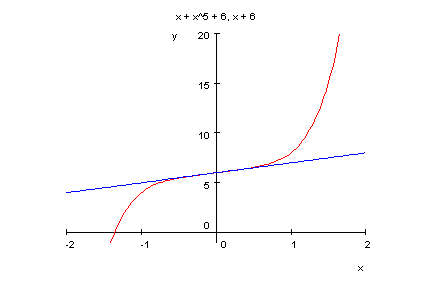
- p18:=x->x^5+x+6;
factor(p18(x));
plotfunc2d(p18(x),x+6,x=-2..2,y=-1..20)
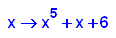
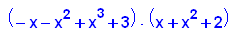

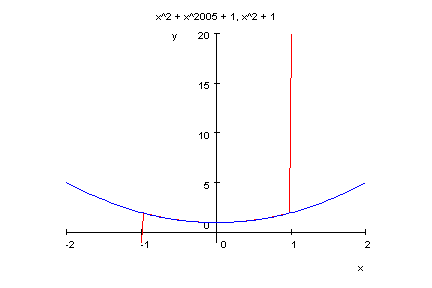
- p19:=x->x^2005+x^2+1;
plotfunc2d(p19(x),x^2+1,x=-2..2,y=-1..20)
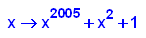

- p19b:=x->x^205+x^2+1;
factor(p19b(x));
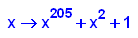 2 2 4 5 7 8 10 11 13
(x + x + 1) (- x + x - x + x - x + x - x + x - x +
14 16 17 19 20 22 23 25 26 28
x - x + x - x + x - x + x - x + x - x +
29 31 32 34 35 37 38 40 41 43
x - x + x - x + x - x + x - x + x - x +
44 46 47 49 50 52 53 55 56 58
x - x + x - x + x - x + x - x + x - x +
59 61 62 64 65 67 68 70 71 73
x - x + x - x + x - x + x - x + x - x +
74 76 77 79 80 82 83 85 86 88
x - x + x - x + x - x + x - x + x - x +
89 91 92 94 95 97 98 100 101
x - x + x - x + x - x + x - x + x -
103 104 106 107 109 110 112 113
x + x - x + x - x + x - x + x -
115 116 118 119 121 122 124 125
x + x - x + x - x + x - x + x -
127 128 130 131 133 134 136 137
x + x - x + x - x + x - x + x -
139 140 142 143 145 146 148 149
x + x - x + x - x + x - x + x -
151 152 154 155 157 158 160 161
x + x - x + x - x + x - x + x -
163 164 166 167 169 170 172 173
x + x - x + x - x + x - x + x -
175 176 178 179 181 182 184 185
x + x - x + x - x + x - x + x -
187 188 190 191 193 194 196 197
x + x - x + x - x + x - x + x -
199 200 202 203
x + x - x + x + 1)
2 2 4 5 7 8 10 11 13
(x + x + 1) (- x + x - x + x - x + x - x + x - x +
14 16 17 19 20 22 23 25 26 28
x - x + x - x + x - x + x - x + x - x +
29 31 32 34 35 37 38 40 41 43
x - x + x - x + x - x + x - x + x - x +
44 46 47 49 50 52 53 55 56 58
x - x + x - x + x - x + x - x + x - x +
59 61 62 64 65 67 68 70 71 73
x - x + x - x + x - x + x - x + x - x +
74 76 77 79 80 82 83 85 86 88
x - x + x - x + x - x + x - x + x - x +
89 91 92 94 95 97 98 100 101
x - x + x - x + x - x + x - x + x -
103 104 106 107 109 110 112 113
x + x - x + x - x + x - x + x -
115 116 118 119 121 122 124 125
x + x - x + x - x + x - x + x -
127 128 130 131 133 134 136 137
x + x - x + x - x + x - x + x -
139 140 142 143 145 146 148 149
x + x - x + x - x + x - x + x -
151 152 154 155 157 158 160 161
x + x - x + x - x + x - x + x -
163 164 166 167 169 170 172 173
x + x - x + x - x + x - x + x -
175 176 178 179 181 182 184 185
x + x - x + x - x + x - x + x -
187 188 190 191 193 194 196 197
x + x - x + x - x + x - x + x -
199 200 202 203
x + x - x + x + 1)
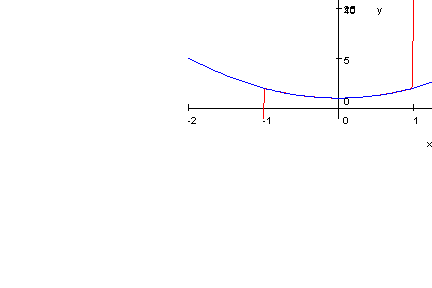

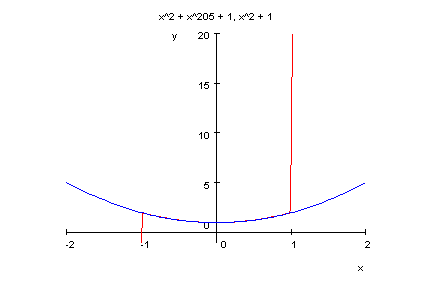
- plotfunc2d(p19b(x),x^2+1,x=-2..2,y=-1..20)

- p20:=x->x^5+x+1;
factor(p20(x));
plotfunc2d(p20(x),x+1,x=-2..2,y=-1..5)
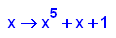
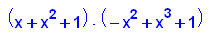

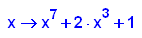
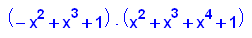
2 2 4 5 7 8 10 11 13 (x + x + 1) (- x + x - x + x - x + x - x + x - x + 14 16 17 19 20 22 23 25 26 28 x - x + x - x + x - x + x - x + x - x + 29 31 32 34 35 37 38 40 41 43 x - x + x - x + x - x + x - x + x - x + 44 46 47 49 50 52 53 55 56 58 x - x + x - x + x - x + x - x + x - x + 59 61 62 64 65 67 68 70 71 73 x - x + x - x + x - x + x - x + x - x + 74 76 77 79 80 82 83 85 86 88 x - x + x - x + x - x + x - x + x - x + 89 91 92 94 95 97 98 100 101 x - x + x - x + x - x + x - x + x - 103 104 106 107 109 110 112 113 x + x - x + x - x + x - x + x - 115 116 118 119 121 122 124 125 x + x - x + x - x + x - x + x - 127 128 130 131 133 134 136 137 x + x - x + x - x + x - x + x - 139 140 142 143 145 146 148 149 x + x - x + x - x + x - x + x - 151 152 154 155 157 158 160 161 x + x - x + x - x + x - x + x - 163 164 166 167 169 170 172 173 x + x - x + x - x + x - x + x - 175 176 178 179 181 182 184 185 x + x - x + x - x + x - x + x - 187 188 190 191 193 194 196 197 x + x - x + x - x + x - x + x - 199 200 202 203 x + x - x + x + 1)

