plotfunc2d(fH(t), f(t), Scaling=Constrained, LegendVisible=FALSE)
Fourier-Reihen, Kippschwingung
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Sept 07 Update 14.05.08
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Dateiname fourier-reihen-kipp.mn
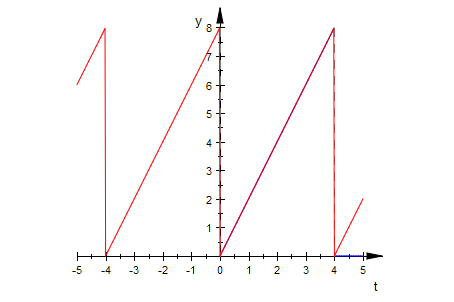
Angabe der Funktion fH in der Hauptperiode.
Definition von f als periodische Funktion.
Ta:=0:Ti:=3: Te:=4:
fH:=t--> piecewise([Ta<=t and t<=Te,2*t],[t>Te,0]) :
f:=t->fH(frac(t/(Te-Ta))*(Te-Ta)):
plotfunc2d(fH(t), f(t), Scaling=Constrained, LegendVisible=FALSE)

Definitionen von Feldern für die Koeffizienten,
übliche Festlegungen T Periode, om =omega= Kreisfrequenz.
n:=10:
a:=array(0..10): b:=array(1..10):
T:=4:
om:=2*PI/T:
Das Verschiebungsglied kann oft auch elementargeometrisch bestimmt werden.
Hier als Dreieck g=4, h=6 -> F=12 und 2/T=2/4=1/2
a[0]:=2/T*int(fH(t),t=Ta..Te)
![]()
So kann man nur die anderen Koeffizienten berechnen.
a[1]:=Simplify(2/T*int(fH(t)*cos(1*om*t),t=Ta..Te));
b[1]:=2/T*int(fH(t)*sin(1*om*t),t=Ta..Te);
![]()
![]()
Automatische Berechnung von n Schwingungen
for k from 1 to 10 do
a[k]:=2/T*int(fH(t)*cos(k*om*t),t=Ta..Te);
b[k]:=2/T*int(fH(t)*sin(k*om*t),t=Ta..Te);
end_for:
Vereinfachen muss extra gefordert werden.
[Simplify(a[k]),Simplify( b[k])] $ k=1..n
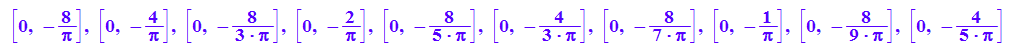
Wenn man mit so einem Werkzeug arbeitet, braucht man über die Gesetzäßigkeit in den
Ausgaben nit nachzudenken. Falls nötig, könnte man es schaffen. Hier ist es leicht: b[k]=-8/(k*PI)
su:=(t,n)->a[0]/2+_plus((a[k]*cos(k*om*t)+b[k]*sin(k*om*t)) $ k=1..n);
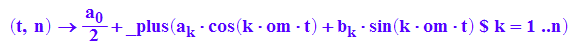
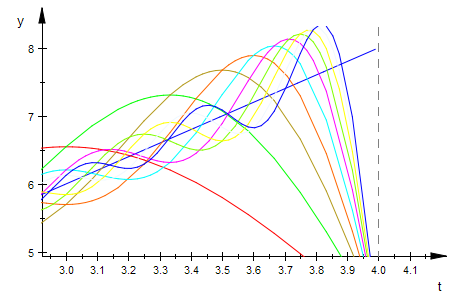
Die Grundschwingung und ihre Achse ist deutlich.
plotfunc2d(fH(t),su(t,n) $ n=1..10,a[0]/2,LegendVisible=FALSE)
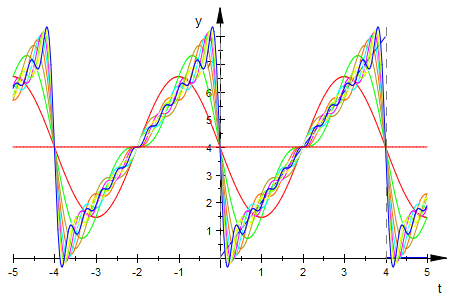
plotfunc2d(su(t,10),f(t), LegendVisible=FALSE)
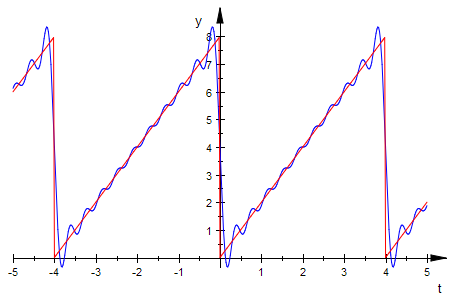
Die Reihen mit 10 Doppeltermen ist von der gegebenen Funktion deutlich zu unterscheiden.
Der interaktiv genommene Ausschnitt zeigt Unterschiede bes. an der Ecken.