tay:=x->expr(taylor(exp(x),x=1,3)):
tay(x)
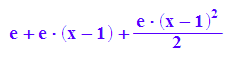
Taylorpolynome und ihre Lage im Vergleich zu f
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Mrz. 05 Update 28.11.05
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Tay.-P. geraden Grades "durchsetzen" i.a. den Graphen von f Mrz. 05 Update 28.11.05
im Entwicklungspunkt.
tay:=x->expr(taylor(exp(x),x=1,3)):
tay(x)
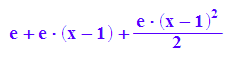
plotfunc2d(exp(x),tay(x),x=-1..3,ViewingBoxYRange=0..10
,LineWidth=1)
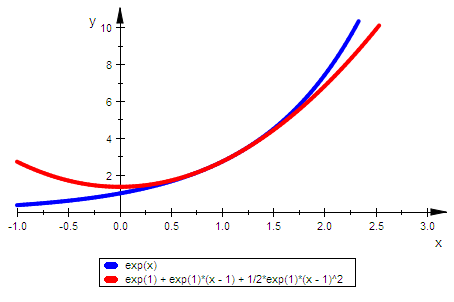
Begründung: p2 sei das Taylorpolynom 2.Grades.
I.A. ist nun q3:=p2-f ein Polynom 3. Grades mit einer
dreifachen Nullstelle im Entwicklungspunkt xo.
q3(x)=a(x-xo)^3+b(x-xo)^4+...=(x-xo)^3*(a+b(x-xo)+...)
War a ungleich 0, dann wechselt q3 das Vorzeichen in xo.
Das heißt gerade, dass p2 f in P durchsetzt.
Entsprechendes gilt für p4, p6 u.s.w.
Nur wenn a=0 ist, stimmt diese Argumentation nicht. (s.u. bei Kosinus)
---------------------------------------------------------------------------------------
Derzimal [Stelle x, f(x), tay(x)] für f(x)=e^x
[float(xx/1000),float(subs(exp(x), x = xx/1000)),
float(subs(tay(x),x=xx/1000))] $ xx=999..1001
![]()
Die Differenzfunktion hat einen Sattel
plotfunc2d(exp(x)-tay(x),x=0.95..1.05,
ViewingBoxYRange=-0.0001..0.0001,LineWidth=1)
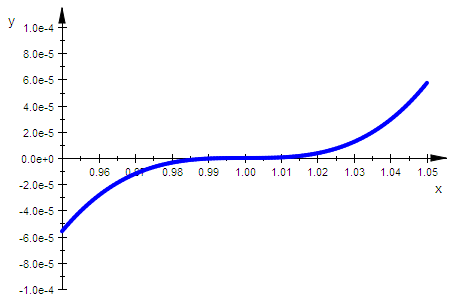
Sinus und Kosinus bilden Sonderfälle, da bei Ihnen alle T-P ungerade
bzw. gerade sind. Daher ist pi-f immer ungerade, bzw. immer gerade.
tay:=x->expr(taylor(sin(x),x=0,3)):
tay(x);
plotfunc2d(sin(x),tay(x),x=-2..3,
ViewingBoxYRange=-1..1,LineWidth=1)
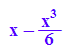
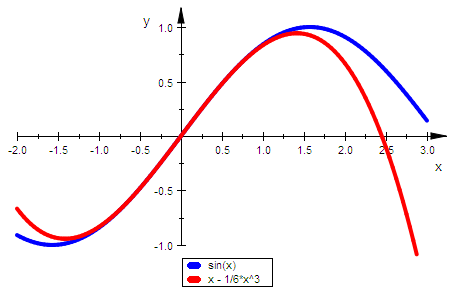
Beim Sinus durchsetzen alle T-P. um O den Graphen.
----------------------------------------------------------------------------
tay:=x->expr(taylor(cos(x),x=0,3)):
tay(x);
plotfunc2d(cos(x),tay(x),x=-2..3,
ViewingBoxYRange=-1..1,LineWidth=1)
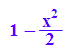
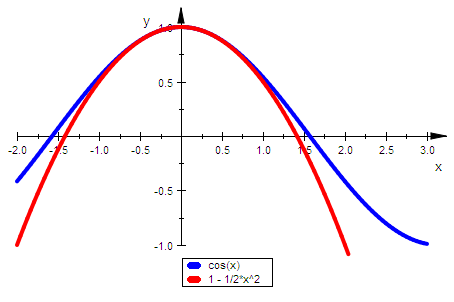
Beim Kosinus durchsetzet kein T-P. um O den Graphen.
---------------------------------------------------------------------------------