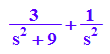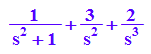
Laplace-Transformationen
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Feb.02 Update 17.05.08
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Formelsammlung An -9- bis -11-
LEVEL 1 Direkte Übersetzungen von MuPAD
Normal-Welt < ------> Laplace-Welt
![]() <---------------->
<---------------->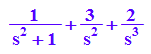
transform::laplace(t^2,t,s)
![]()
transform::invlaplace(%,s,t)
![]()
transform::laplace(t^2+3*t+sin(t),t,s)
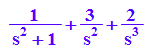
transform::invlaplace(%,s,t)
![]()
Partialbruchzerlegung
term:=1/((s-3)*(s+4))
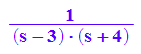
partfrac(term)
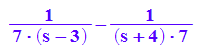
term:=1/((s-3)^2*(s^2+4))
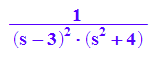
partfrac(term)
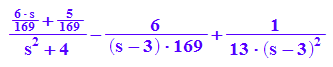
LEVEL 2 Berechnungen gemäß der Definition
f:=t->t+sin(3*t)
![]()
lapint:=int(f(t)*exp(-s*t), t=0..c,Continuous)
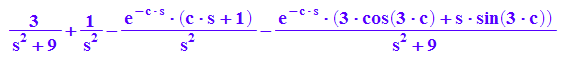
asume(s,Type::NonNegative):asume(c,Type::Real)
:limit(lapint,c=infinity)

Klappt nicht im hinteren Term, aber man sieht ja, dass der Term mit e^-cs gegen Null geht.
erg:=lapint[1]+lapint[2]
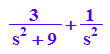
partfrac(erg)
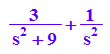
Damit kommt heraus, was herauskommen musste:
transform::laplace(f(t),t,s)