arch:=plot::Polar([t,t], t=0..20):plot(arch)
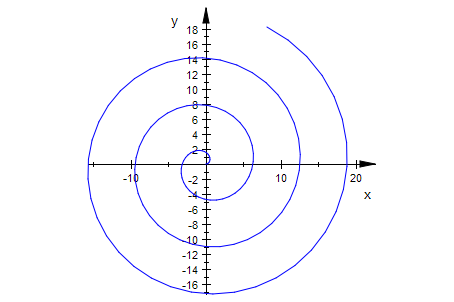
Archimidische Spirale als CD-Spur
Prof. Dr. Dörte Haftendorn, mit MuPAD, Mrz. 07 nach eine Emailanfrage von M.Thewes
Web: www.mathematik-verstehen.de https://mathe.web.leuphana.de
arch:=plot::Polar([t,t], t=0..20):plot(arch)

Bei der Archimedischen Spirale r= a*t ist der Abstand der Spiralarme a*2*PI.
Bei einer CD mit der beschreibenen Spurbreite g und der Zwischenraumbreite g
gilt
a*2*PI=2*g
![]()
Die CD-Spirale ist also:
r:=t->g/PI*t
![]()
Bogenlänge in Polarkoordinaten ist dann
hold(int(sqrt(r(t)^2+r'(t)^2), t))
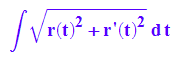
r(t)^2+r'(t)^2
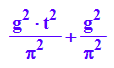
L:=g/PI*int(sqrt(t^2+1), t)
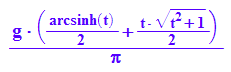
Als bestimmtes Integral:
LCD:=g/PI*int(sqrt(t^2+1), t=0..k*2*PI)
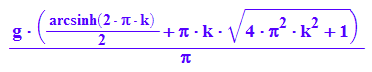
Eine CD sei von einem Radius von 2.1 cm bis zu einem Radius von 5.8 cm bespielt.
Das sind folgende Anzahlen Spiralenrunden:
2.1/0.00032
![]()
5.8/0.00032
![]()
float(0.00016/PI*int(sqrt(t^2+1), t=6562*2*PI..(18125)*2*PI))
![]()
Dieses ist also die Länge der CD-Spirale.
------------------------------------------------------------------------
Abschätzung:
Die CD-Spur hat also etwa 11000 Windungen und fängt recht weit außen an,
daher ist sie im Verhältnis zu ihrer Dicke von 2g=2*0.00016 cm kaum gekrümmt.
Daher könnte man sie zum Rechteck aufbiegen. Diese Rechteck hat folgende Fläche:
einerseits A=Spurlänge*Gesamtspurbreite
andererseits= Fläche des beschiebenen Kreisrings der CD
A:=PI*(ra^2-ri^2)
![]()
Damit ergibt sich für die Länge der Spur:
3.1416*(5.8^2-2.1^2)/0.00032
![]()
-------------------------------------------------------
Beweis der Abschätzung mit einer Abschätzung der obigen Integration:
Der Sinushyperbolikus ist eine e-Funktion, Arkussinushyperbolikus also für
große Argumente etwa eine ln_funktion, wächst also kaum:
float(arcsinh(6562*2*PI));
float(arcsinh((18125)*2*PI));
![]()
![]()
g und die Division durch 2*PI machen diesen Termteil winzig:
float(0.00016/2/PI*(-arcsinh(6562*2*PI)+arcsinh(18125*2*PI)));
![]()
Die 1 unter der Wurzel kann für k im Tausenderbereich vernachlässigt werden)
LCD:=g*2*PI*ka^2-g*2*PI*ki^2
![]()
Nun ist
ri=2*g*ki;
ra=2*g*ka;
![]()
![]()
Also folgt
LCD:=PI*ri*(ri/(2*g))-PI*ra*(ra/(2*g));
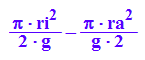
und das ist genauso wie die obige Abschätzung.