Lineares Optimieren: Mathöl-Raffinerie
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
(Elem. der Math. 9, Ausg 1990, S. 49, nachempfunden)
Langversion mit zwei Zeichenmethoden
x= Masse arabisches Öl in t
y= Masse amerikanisches Öl in t
tgl. Mindestmengen: Leichtöl 120 t, Schweröl 105 t, Benzin 240 t
Preise: arabisches € Öl 400 €/t, amrikanisches Öl 300 €/t
kosten:= 400*x+300*y;
leicht:= 120<=0.4*x+0.1*y;
schwer:= 105<=0.1*x+0.3*y;
benzin:= 240<=0.4*x+0.3*y;
![]()
![]()
![]()
![]()
Es gibt in MuPAD 4 eine Möglichkeit, Ungleichungen direkt zu visualisieren.
Ausfühlich erläutert auf der Seite: Ungleichungen.
Durch Einstelung der Transparenz auf 0.2 kann man das gesuchte konvexe Gebiet als Überlagerungsgebiet aller Farben erkennen.
pil:=plot::Inequality(leicht,x=0..1100,y=0..1300,
FillColorTrue=[0,0,1,0.2],FillColorFalse=[1,1,1,0.2] ,Mesh=[300,300]):
pis:=plot::Inequality(schwer,x=0..1100,y=0..1300,
FillColorTrue=[0,1,0,0.2],FillColorFalse=[1,1,1,0.2] ,Mesh=[300,300]):
pib:=plot::Inequality(benzin,x=0..1100,y=0..1300,
FillColorTrue=[1,0,1,0.2],FillColorFalse=[1,1,1,0.2] ,Mesh=[300,300]):
plot(pil,pib,pis)
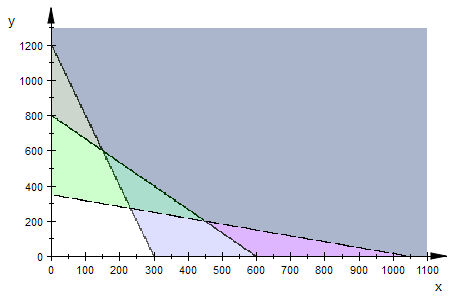
Da im schulischen Rahmen aber sowieso die Randgleichungen und deren Graphen ein Rolle spielen, ist im Folgenden der konventionelle Gang vorgeschlagen.
fl:=x->-4*x+120/0.1;
fs:=x->-1/3*x+105/0.3;
fb:=x->-4/3*x+240/0.3;
ziel:=x->-4/3*x+Kzt*10000/300;
fl(x),fs(x),fb(x),ziel(x)
![]()
![]()
![]()
![]()
![]()
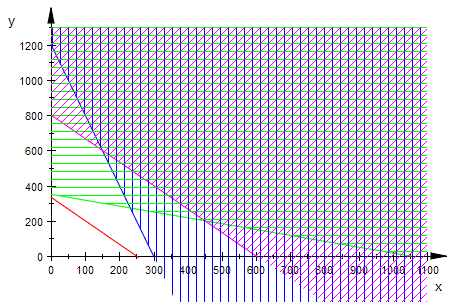
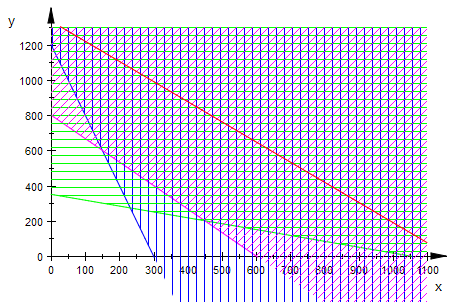
Hier wird nun die Hatch-Funktion für die Flächen verwendet.
Schraffur oder transparente Vollfarben kann man bei beiden Arten nehmen.
gfl:=plot::Function2d(fl,x=0..1100,LineColor=[0,0,1]):
gfs:=plot::Function2d(fs,x=0..1100,LineColor=[0,1,0]):
gfb:=plot::Function2d(fb,x=0..1100,LineColor=[1,0,1]):
pl:=plot::Hatch(gfl,1300,FillPattern=VerticalLines,FillColor=[0,0,1]):
ps:=plot::Hatch(gfs,1300,FillPattern=HorizontalLines,FillColor=[0,1,0]):
pb:=plot::Hatch(gfb,1300,FillPattern=DiagonalLines,FillColor=[1,0,1]):
pk:=plot::Function2d(ziel(x),x=0..1100,Kzt=10..40, LineColor=[1,0,0]);
plot(gfl,gfs,gfb,pl,ps,pb,pk,ViewingBox=[0..1100,0..1300]);
plot(gfl,gfs,gfb,pil,pis,pib,pk,ViewingBox=[0..1100,0..1300]);
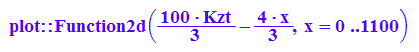
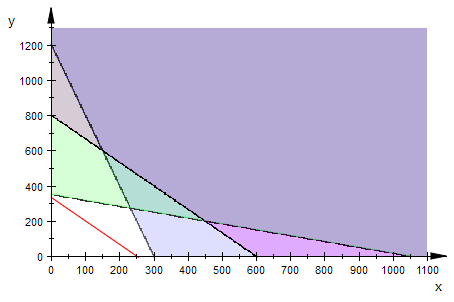
Merkwürdigerweise ist die Bewegung der Zielgeraden im
Inequality-Fall (unten) langsamer.
######################################################
Die Zielgerade ist parallel zur Bezingerade. Also ist kann die Raffinerie ihren Rohöleinkauf beliebig mischen in folgendem Bereich:
minx1:=solve(fl(x)=fb(x),x)[1]: miny1:=fb(minx1):
k1:=kosten|{x=minx1,y=miny1}: [minx1,miny1,"Kosten ",k1];
minx2:=solve(fs(x)=fb(x),x)[1]: miny2:=fb(minx2):
k2:=kosten|{x=minx2,y=miny2}: [minx2,miny2,"Kosten ",k2];
fb(x)
![]()
![]()
![]()
Zwischen x=150 t und x=600 t arabischen Öls müssen sie y=![]() t
t
amerikanischen Öls kaufen.
--------------------------------------------------------------------------------
Falls nun aber das amerikanische Öl teurer wird, 350 €/t, wird die Zielgerade flacher und es ist klar, dass sie dann möglicht viel arabisches Öl nehmen.
ziel2:=x->-4/3.5*x+Kzt*10000/300;
pk:=plot::Function2d(ziel2(x),x=0..1100,Kzt=10..40, LineColor=[1,0,0]):
plot(gfl,gfs,gfb,pl,ps,pb,pk,ViewingBox=[0..1100,0..1300])
![]()
[minx2,miny2,k2]
![]()
Das ist nun der billigste erzielbare Rohöleinkauf unter den gegebenen Bedingungen.