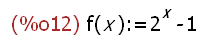
Mersenne Primzahlen+vollkommene Z.

Prof. Dr. Dörte Haftendorn, Jan 2012, www.mathematik-verstehen.de

(%i12) f(x):=2^x-1 /* Mersenne-Zahlen*/;

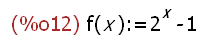
Die Vorgänger von Zweierpotenzen heißen "Mersenne-Zahlen".

Darunter sind einige Primzahlen, sie heißen "Mersenne-Primzahlen"

"Vollkommene Zahlen" sind die, die gleich der Summe ihrer echten Teiler sind.

0.1 Die zur Mersenne-Primzahlen gebildeten Dreiesckszahlen v(mp)
sind "vollkommene Zahlen".
Andere gerade vollkommene Zahlen gibt es nicht.
Ungerade vollkommene Zahlen kennt man
unter 10^500 nicht.

Info: Wikipedia: vollkommene Zahlen Mersenne Primzahlen

(%i57) v(x):=2^(x-1)*(2^x-1) /*Dreieckszahlen aus Mersenne-Zahlen*/;

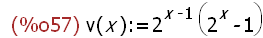
Vollkommen sind diese also nur, wenn die darüber stehende Mersenne-Zahl
eine Primzahl ist.

Im Folgenden stehen übereinander:
Primzahl, Mersenne-Zahl,
Kleiner Fermat für diese: Primzahlkandidat falls 1,
Faktorisierung der Mersenne-Zahl, falls zerlegt: keine Mersenne-Primzahl
Kandidat für Vollkommene Zahl: ja falls f(p) Mersenne-Primzahl.

(%i58) p:2;f(p); power_mod(2,f(p)-1,f(p));factor(f(p));v(p);

(%i79) p:3;f(p); power_mod(2,f(p)-1,f(p));factor(f(p));v(p);

(%i84) p:5;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i94) p:7;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i99) p:11;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i104) p:13;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

--> p:17;f(p); mod(2^(2^p),p);factor(f(p));v(p);

--> p:19;f(p); mod(2^(2^p),p);factor(f(p));

(%i109) p:23;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));

(%i113) p:29;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i118) p:31;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i123) p:37;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i128) p:61;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i133) p:67;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i138) p:87;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i143) p:89;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i148) p:101;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

(%i153) p:107;f(p); power_mod(3,f(p)-1,f(p));factor(f(p));v(p);

es folgen 127, 521,607,1279,2203.... als weitere Mersenne Primzahlen

Die folgende Zahl hat man bis 1932 für eine Merenne-Primzahl gehalten.

(%i160) f(257);

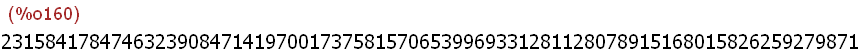
(%i167) p:257;power_mod(2,f(p)-1,f(p));power_mod(3,f(p)-1,f(p));

Aber der kleine Fermat mit Basis 3 hätte es ans Licht gebracht.

--> /* factor(mp257) */;

Suche nach 5 Minuten abgebrochen

0.2 Kleiner Satz von Fermat
p prim folgt mod(a^(p-1),p)=1

(%i177) mod(2^12,13); p:11;f(p);power_mod(2,f(p)-1,f(p));power_mod(3,f(p)-1,f(p));

Bein Kleinen Fermat ist man gut beraten, beim Ergebnis 1 auch andere
Basen auszuprobieren.

(%i182) p:13; f(p);power_mod(2,f(p)-1,f(p));power_mod(3,f(p)-1,f(p));