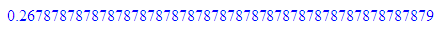DIGITS:=40 //Dezimalen-Anzeige vergrößern

Periodische Kommazahlen
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Mai 2004
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
DIGITS:=40 //Dezimalen-Anzeige vergrößern

float(1/17)
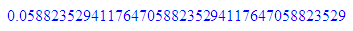
So kann man die Periodenlänge ablesen.
Experimentiere mit 1/n , wie lang ist jeweils die Periode?
n:=13: [1/n,float(1/n)]
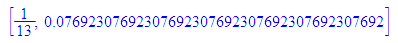
Versuche abbbrechende und nicht abbrechende Kommazahlen zu sortieren.
Bei welchen Nennern n bricht die Kommazahl 1/n ab?
n:=2^3*5^7: [1/n,float(1/n)]
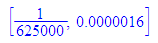
//--------------------------------------------------------
Experimentiere: bei welchen Nennern n erhält man echte Vorperioden?
Vorperioden sind hinter dem Komma Ziffern ungleich Null, die nicht in der Periode vorkommen
n:=16*17: [1/n,float(1/n)]

//-------------------------------------------------------
Rückverwandlung von periodischen Kommazahlen in Brüche
DIGITS:=8:
[1/(10^n-1),float(1/(10^n-1))] $n=1..5

[23/(10^n-1),float(23/(10^n-1))] $n=2..5
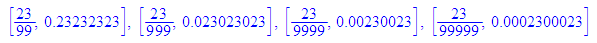
[2347/(10^n-1),float(2347/(10^n-1))] $n=4..7

Also erzeugen die Nenner mit lauter Neunen Perioden, die genau dem Zähler entsprechen, aufgefüllt mit Nullen.
Die Periodenlänge ist gleich der Anzahl der Neunen.
Umgekehrt: Für die Rückverwandlung sofort-periodischer Dezimalzahlen muss man offenbar die
Periode als Zähler nehmen und als Nenner soviele Neunen wie die Periodenlänge angibt.
DIGITS:=40:
[0.123456712345671234567,1234567/9999999,float(1234567/9999999)]
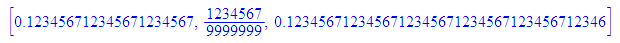
Kommazahlen mit Vorperiode
Man muss den Vorperiodenteil abtrennen.
[0.345123456712345671234567,345,"+",1234567/9999999];
[345+1234567/9999999000,float(345+1234567/9999999)/1000]
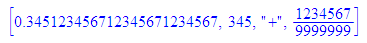
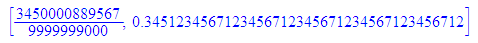
float(0.345+1234567/9999999000)
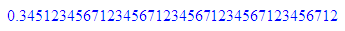
Mit dem Befehl des CAS bekommt man nur Näherungslösungen:
numeric::rationalize(0.34512345671234567)
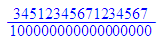
float(%)
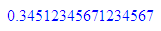
588235294117647/9999999999999999
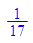
//------------------------------------------------------
Die Periodenlänge teilt Phi(n)=Euler(n), wenn N teilerfremnd zu 10 ist.
Bestätigen Sie das für etliche Beispiele.
Beschaffung von EulerPhi
numlib::phi(3*11*13)

n:=3*11*13: [1/n,float(1/n)]

Periodenlänge 6 und 6 teilt tatsächlich 240.
Experimentierfeld:
float(1/137)
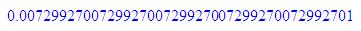
float(1/(2*137));float(1/(16*137));
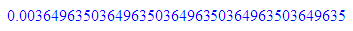
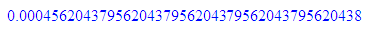
float(1/17);float(1/(16*17));
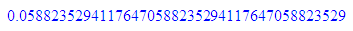
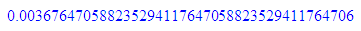
float(1/11);float(1/(4*11));float(1/(44*11));
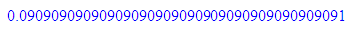
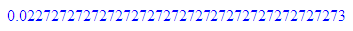
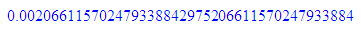
numlib::phi(44)
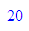
DIGITS:=52
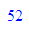
float(1/3);float(1/(4*3));float(1/(7*17));
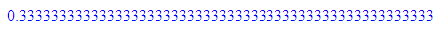
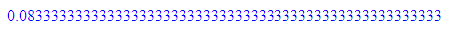
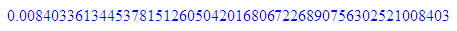
6*16

float(1/(11*11));float(1/(7*19));float(1/(11*17));
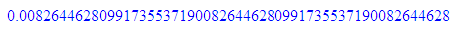
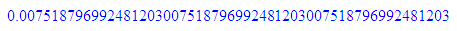
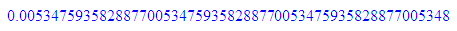
numlib::phi(121)
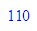
float(1/(16*11));float(1/(4*3));float(1/(256*17));
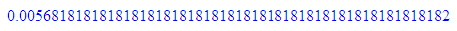
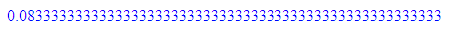
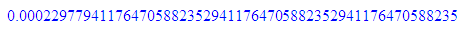
float(1/256)
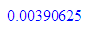
float(1/4);float(1/44)
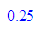
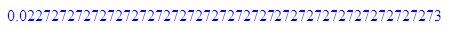
float(1/4);float(1/(4*17));float(1/17);float(1/34)
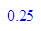
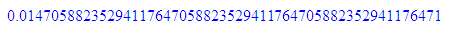
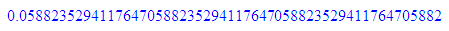
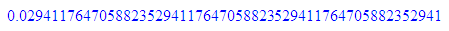
float(1/29);float(1/(4*29));float(1/(16*29));float(1/(3125*29))
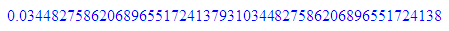
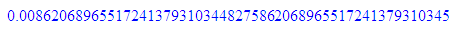
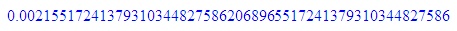
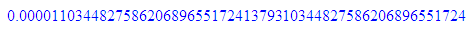
1/5^5;float(%)
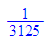
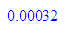
1/99;float(%)
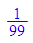
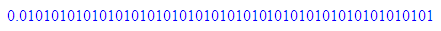
34*78
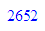
2652/9900
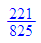
float(221/825)