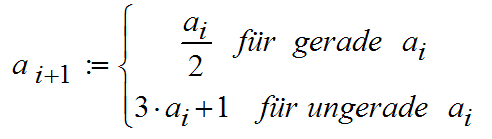
Das Halteproblem, Entscheidbarkeit:
Prof. Dr. Dörte Haftendorn, MuPAD 4, Jan. 07 Update 07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Die "Collatz-Folge" oder "3n+1-Folge" ist geeignet, einige grundlegende Erkenntnisse
zum Halteproblem und zur Entscheidbarkeit anzuregen:
Starte mit n. 
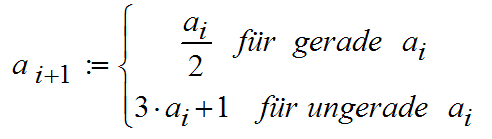
f:=proc(n)
local s;
begin
s:=[n];
while n>1 do
if (n mod 2)=0 then
n:=n div 2;
else
n:=3*n+1;
end_if;
s:=s.[n];
end_while;
//print(s,nops(s));
return( s);
end_proc:
Ausgabe-Version
fpr:=proc(n)
local s;
begin
s:=[n];
while n>1 do
if (n mod 2)=0 then
n:=n div 2;
else
n:=3*n+1;
end_if;
s:=s.[n];
end_while;
print(s,nops(s));
//return( s);
end_proc:
Angegeben wird die Folge als Liste und deren Elementezahl.
fpr(k) $ k=3..20
[3, 10, 5, 16, 8, 4, 2, 1], 8
[4, 2, 1], 3
[5, 16, 8, 4, 2, 1], 6
[6, 3, 10, 5, 16, 8, 4, 2, 1], 9
[7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 17
[8, 4, 2, 1], 4
[9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 20
[10, 5, 16, 8, 4, 2, 1], 7
[11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 15
[12, 6, 3, 10, 5, 16, 8, 4, 2, 1], 10
[13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 10
[14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 18
[15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1], 18
[16, 8, 4, 2, 1], 5
[17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 13
[18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1],
21
[19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1],
21
[20, 10, 5, 16, 8, 4, 2, 1], 8
Erstaunlicherweise dauert es sehr verschieden lange bis 1 erreicht wird.
Und 1 wird hier immer erreicht.
---------------------------------------------
Visualisierung:
plot(plot::Listplot(f(14)),
plot::Listplot(f(15), LineColor=[1,0,0,0.5]),
plot::Listplot(f(17), LineColor=[0,1,0,0.5]),
plot::Listplot(f(18), LineColor=[1,0,1,0.5]),
LineWidth=0.8);
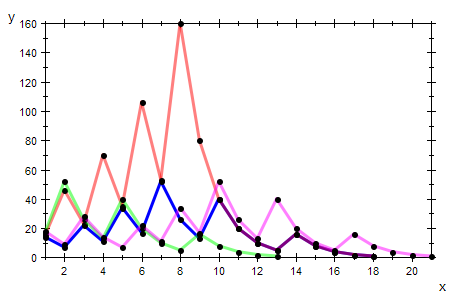
Die Folgen, die dicht beieinander starten entwickeln sich dennoch ganz verschieden.
---------------------------------------------------------------------
Test für eine große Zahl:
plot(plot::Listplot(f(1000)));
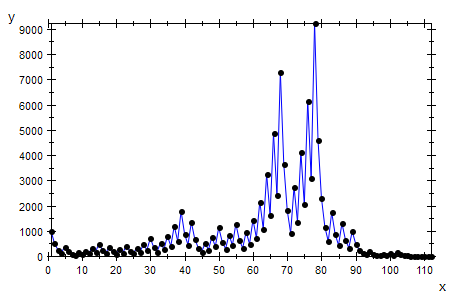
Mit Ansicht der Folgenglieder:
Nachdem schon ganz bescheidene Größe erreicht war (47) geht es nochmal richtig in die Höhe.
fpr(1000);
[1000, 500, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242,
121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350,
175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167,
502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479,
1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734,
1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433,
1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53,
160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1], 112
In der Schlussphase kommt 46 vor statt 47, danach ist es bald zuende.
plot(plot::Listplot(f(27)),plot::Listplot(f(1000),LineColor=[1,0,0]));
##########################################################################
Was lehrt dieses Beispiel:
Durch Hinsehen und Beobachten kann man nicht entscheiden, ob die Folge auf 1 zuläuft oder nicht, ob also das
Programm anhält oder nicht.
Was man sonst noch weiß:
Es ist noch keine Startzahl gefunden worden, bei der 1 nicht erreicht wird.
Es hat noch niemand beweisen können, dass immer 1 erreicht wird.
Die mathematische Analyse des Programms zeigt nur die Umsetzung der Definition, sonst nichts.
Eine irgenwie geartete "softwaremäßige Anlalyse" , die das Halteproblem für dieses Programm entscheiden kann, müsste da viel mehr leisten, als die Mathematiker bis jetzt geschafft haben.
Dafür haben die Mathematiker aber folgendes bewiesen:
Es kann keinen Algorithmus geben, der das sogenannte "Halteproblem" löst.
Hiermit ein Programm gemeint, das für alle vorgelegten Programme und alle zulässigen Eingaben über deren Anhalten entscheiden kann.
Beweis (indirekt): HP sei so ein Programm, das das Halteproblem löst. Dann baut man um HP ein Programm K, dass anhält, wenn HP "nein" ausgibt und das nicht anhält, wenn HP "ja" ausgibt. K nimmt als Eingabe auch Programme entgegen, die es dann an HP in seinem Innern weitergibt.
Wenn nun K seinen eigenen Programmcode liest, verarbeitet HP den und antwortet auf eine von zwei Arten:
entweder mit "ja, K hält an" , dann aber hält K nicht an, also Widerspruch erzeugt.
oder mit "nein, K hält nicht an, dann aber hält K an, also auch Widerspruch erzeugt.
Also kann kein Programm HP geben, das das Halteproblem immer löst. q.e.d.
-----------------------------------------------------------------------------------------------------------------------
Weitere Beispiele
plot(plot::Listplot(f(100002)));
fpr(100002);
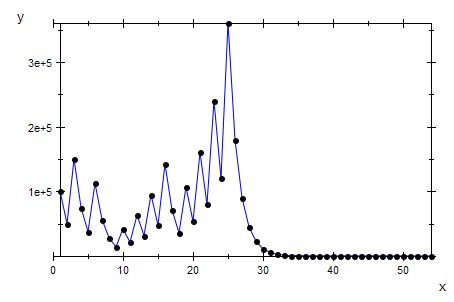
[100002, 50001, 150004, 75002, 37501, 112504, 56252, 28126, 14063, 42190,
21095, 63286, 31643, 94930, 47465, 142396, 71198, 35599, 106798, 53399,
160198, 80099, 240298, 120149, 360448, 180224, 90112, 45056, 22528, 11264,
5632, 2816, 1408, 704, 352, 176, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20,
10, 5, 16, 8, 4, 2, 1], 54