lnVon_nMinus1Fakultaet:=n->(n-1/2)*ln(n-1)-n+1+ln(sqrt(2*PI))
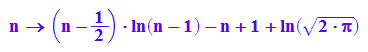
Zeitkomplexität
Prof. Dr. Dörte Haftendorn, MuPAD 4, Jan. 07 Update 07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Diverse Komplextitätsfunktionen beim Sortieren:
Stirlingformel
lnVon_nMinus1Fakultaet:=n->(n-1/2)*ln(n-1)-n+1+ln(sqrt(2*PI))
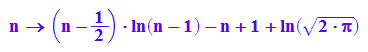
[float(lnVon_nMinus1Fakultaet(n)) $ n=10..15]
![]()
float(ln((n-1)!)) $n=10..15
![]()
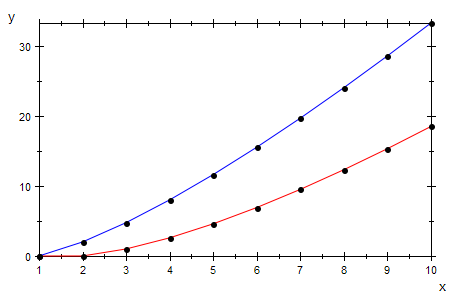
plotfunc2d(n*log(2,n),1/ln(2)*lnVon_nMinus1Fakultaet(n),n^2,n=1..150)
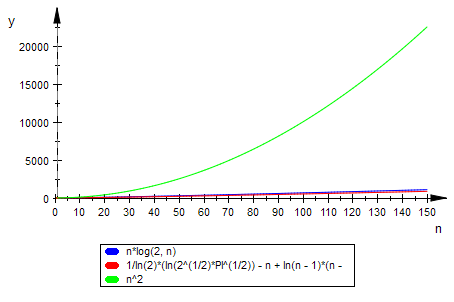
Mit der log(2,(n-1)!) und der nachfolgenden Version klappt es nicht.
plotfunc2d(float( eval(1/ln(2)*ln((n-1)!))),n=0..10)
nichts zu sehen, daher habe ich oben die Stirlingformel verwendet.
Mit Listen geht es auch mit der Originalformel:
liplfak:=plot::Listplot( [ (log(2,(n-1)!) $ n=1..10) ], LineColor=[1,0,0]):
liplnlo:=plot::Listplot( [n*log(2,n) $ n=1..10], LineColor=[0,0,1]):
plot(liplfak,liplnlo)
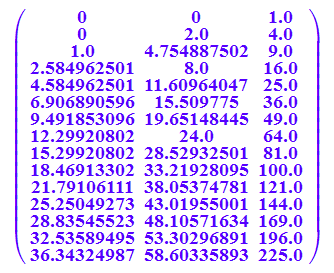
matrix([float([log(2,(n-1)!),n*log(2,n),n^2]) $ n=1..15])
Weitere Komplextiätsfunktionen und Zeiten
[1,60,60*60,60*60*24,60*60*24*365,60*60*24*365*3200]
![]()
Anzahl der Sekunden in 1 s,1 min,1 h,1 d, 1a, seit Ramses II
sekProJahr:=31.536000*10^6// 31 Millionen
![]()
sekSeit_homo_erectus:=sekProJahr*600000
![]()
10^20/sekProJahr
![]()
10^20 s sind 3 Billionen Jahre
sekSeitUrknall:=sekProJahr*13*10^9
![]()
weniger als 10^18 s seit dem Urknall
minProJahr:=24*365*60
![]()
Betrachtung der exponentiellen und super-exponentiellen Wachstumsfunktionen
gegenüber den polyminialen Wachstumsfunktionen.
Wir betrachten Superrechner (Parallelrechner, Rechnercluster...) mit
200 Teraflops= 200 10^12 Gleitkommaoperationen pro sek.
t0:=5*10^(-15):
plotfunc2d(t0*n^n,t0*2^n,t0*n^5,t0*n^2,
8.6*10^10,31*10^12,10^17,
sekSeit_homo_erectus*10^6,4*10^23,
n=1..1000,ViewingBoxYRange=5*10^-15..10^40 ,
LineWidth=0.8,CoordinateType = LogLog, LegendVisible=FALSE)
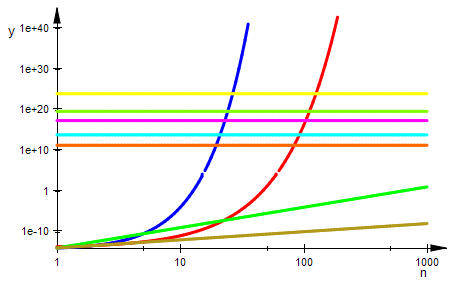
n= Umfang der Eingabe
Ordinate= Zahl der Mikrosekunden Rechenzeit bei 200 10^12 Operationen pro sek,
also ein Operation in t0=5 10^-15 s
Waagerechten:Mikrosek pro Tag, Mikrosek pro Jahr, Mikrosek seit Ramses II,
Mikrosek seit Homo Erectus, Mikrosek seit Urknall.