Analysis II Darstellungen

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Dez 2010

0.1 Handling

0.2 Inhalt

1 Parameterdarstellungen
2 Polarkoordinaten
3 Implizite Darstellungen

1 Parameterdarstellungen

1.1 Darstellung in wxplot

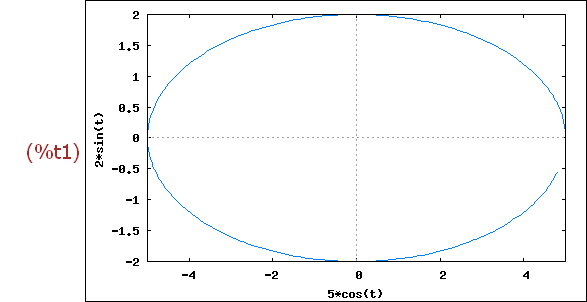
(%i1) wxplot2d([ ['parametric, 5*cos(t), 2*sin(t), [t, 0, 6], [nticks, 300]]], [x,-5,5])$

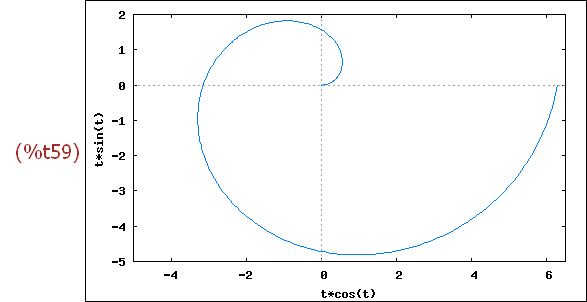
(%i59) wxplot2d([ ['parametric, t*cos(t), t*sin(t), [t, 0, 2*%pi], [nticks, 300]]], [x,-5,6.5])$

1.2 Dartellung in Maxima mit gnuplot

Erklärungen zum Gebrauch bei Datei "Sinustorte" in Analysis 3d.
Diese Methode halte ich für flexibler, da die Möglichkeiten
von wxplot doch sehr begrenzt erscheinen. Zumindest erhält man
Hilfen nur zu dieser ausführlicheren Version.

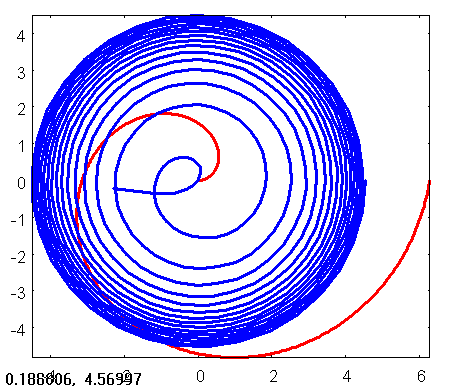
(%i63) load(draw)$
kurven:gr2d(nticks=500,line_width=3,color=red,
                 parametric(t*cos(t), t*sin(t), t, 0, 2*%pi) , color=blue,
                 parametric(log(t)*cos(t), log(t)*sin(t), t, 0.1, 30*%pi) )$
parabel:gr2d(line_width=3,color=green,
                 parametric(t, t^2, t, -2,2))$

(%i62) draw(kurven)$

Figure 1:

Die Logik ist: Das Package draw wird geladen. Darin sind viele
nützliche Befehle. Mit ihnen erzeugt man mit gr2d() und gr3d()
Grafikobjekte, die dann von draw(....) dargestellt werden.
Was in ein gemeinsames Bild soll, muss in demselben Grafikobjekt
stehen. Bekommt draw mehrere Objekte, werden sie untereinander
dargestellt.

(%i67) draw(kurven,parabel)$

Figure 2:

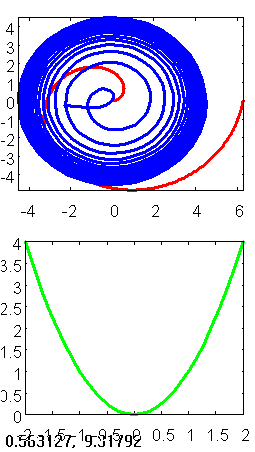
2 Polarkoordinaten

2.1 ungünstige Version

Im Menu Plotten bei Optionen "setpolar" wählen

(%i28) wxplot2d([phi*phi], [phi,0,2*%pi],[x,-15,9],[y,-25,5],
 [gnuplot_preamble, "set polar; set zeroaxis;"])$

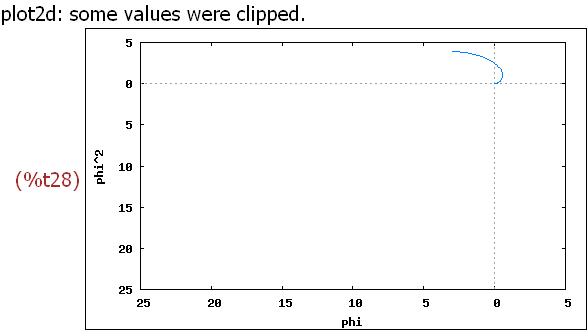
Diese Darstellung ist absolut unbefriedigend, denn es wird längst
nicht alles dargestellt.Der Graph müsste einmal herum gehen.

2.2 Günstige Version mit draw2d

--> load(draw)$

(%i47) draw2d(user_preamble = "set grid polar",
             nticks = 300, xrange = [-15,40], yrange = [-25,5],
             color = blue, line_width = 3,
             polar(ph*ph,ph,1,2*%pi) )$

Figure 3:

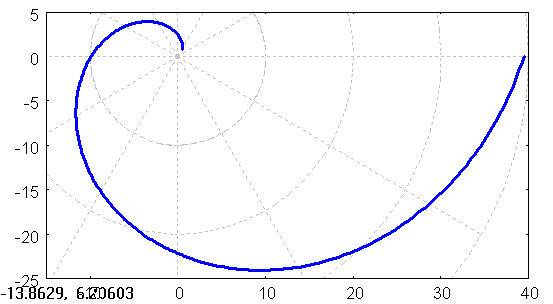
(%i73)
draw2d(user_preamble = "set grid polar",
             nticks = 200, xrange = [-5,5], yrange = [-5,5],
             color = blue, line_width = 3,
             polar(10/theta,theta,1,10*%pi) ,
             color = red, line_width = 3,
             polar(log(ph),ph,1,2*%pi)
)$

Figure 4:

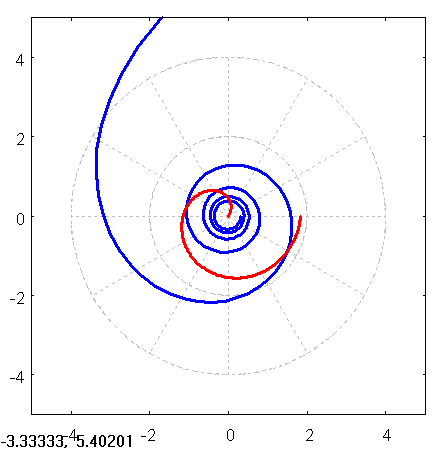
Hier hat man wesentlich mehr Möglichkeiten.

2.3 Version mit Grafikobjekten

(%i69) spira:gr2d(user_preamble = "set grid polar",
             nticks = 200, xrange = [-5,5], yrange = [-5,5],
             color = blue, line_width = 3,
             title = "Hyperbolic Spiral",
             polar(10/theta,theta,1,10*%pi) )$
draw(spira)$

Figure 5:

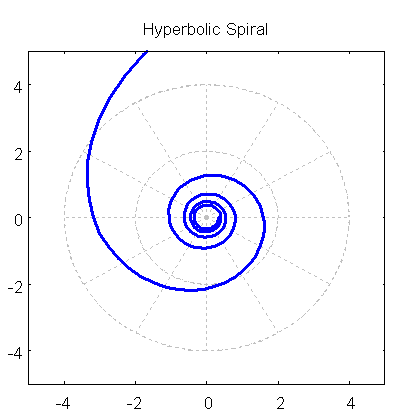
Diese Version erlaubt die größte Flexibilität.
Insbesondere kann man mehrere Darstellungen in
ein Grafikobjekt schreiben.

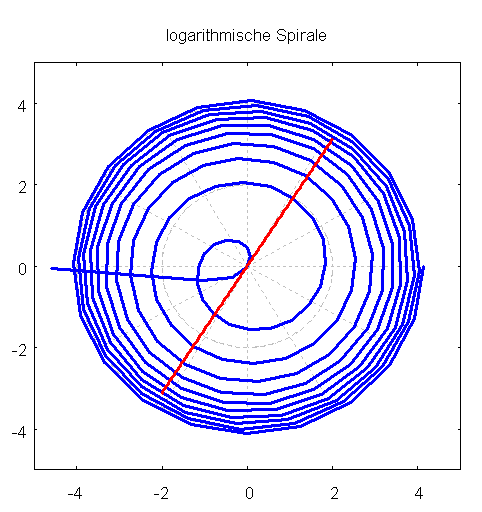
--> loga:gr2d(user_preamble = "set grid polar",
             nticks = 200, xrange = [-5,5], yrange = [-5,5],
             color = blue, line_width = 3,
             title = "logarithmische Spirale",
             polar(log(theta),theta,0.01,20*%pi) ,
             color = red, line_width = 3,
             parametric(t,tan(1)*t,t,-2,2)
 )$
draw(loga)$

Figure 6:

3 Implizite Darstellungen

3.1 Implizit 2D

(%i48) load(draw)$

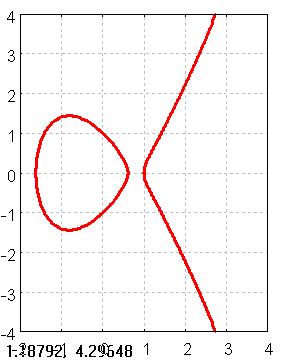
(%i57) draw(gr2d(line_width=3, color=red,grid=true,
             implicit(y^2=x^3-2*x+1, x, -2,4, y, -4,4)
            ))$

Figure 7:

3.2 Implizit 3D und Parameterkurven 3D

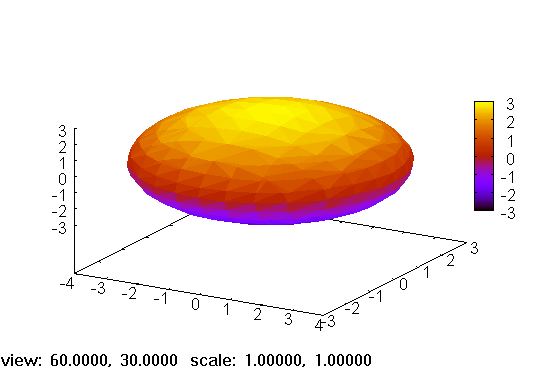
(%i49) elli:gr3d(enhanced3d=true,implicit((x^2)/16+(y^2)/9+(z^2)/9=1,
              x,-4,4,y,-3,3,z,-3,3))$
draw(elli)$

Figure 8:

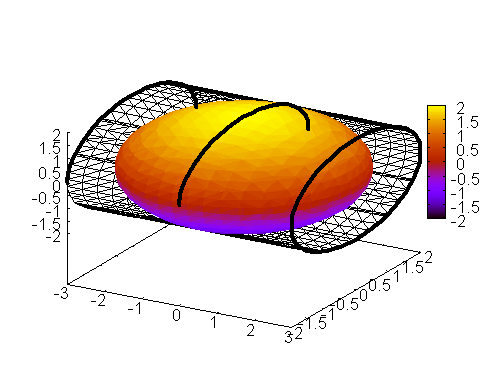
(%i51) draw(gr3d(enhanced3d=false,x_voxel=15, y_voxel=15, z_voxel=15,
                 implicit( 1/4*y^2 +1/4* z^2=1, x, -3, 3,y, -2, 2,z,-2,2),
                 enhanced3d=true,
                 implicit(1/9*x^2 +1/4*y^2 +1/4* z^2=1, x, -3, 3,y, -2, 2,z,-2,2),
                 enhanced3d=false, color=black, line_width=4,
                 parametric(3,2*cos(t),2*sin(t),t,0,2*%pi),
                 parametric(0,2*cos(t),2*sin(t),t,0,1*%pi),
                 parametric(-3,2*cos(t),2*sin(t),t,0,1*%pi)
                ) )$

Figure 9: