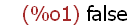
Maxima als Rechner
Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010
Noch nicht in Deutsch adaptiert. Dies ist aber i.W. selbsterkärend
0.1 Autor und seine Daten
Maxima As a Calculator
Abstract
Maxima may be used for making numerical calculations using the numerals (called
"atoms") within Maxima. Numeral atoms are symbols for numbers in the context of
numerical computation -- everything in Maxima is essentially a symbolic expression.
This includes the usual sets of numbers and operations used in typical calculations
-- integers, rational numbers, and "real numbers" which as will be demonstrated
are actually rational number approximations in the form of decimal numerals. Thus
Maxima may be used for the same simple purposes as a hand-held calculator.
-----------------------------------------------------------------------------------------------------------------------
Notes:
This session is not comprehensive or exhaustive, however some of the basic
Maxima functions and features are demonstrated. Please note that there may
be alternative ways to form the Maxima statements of this session. Please
refer to the Maxima documentation and the wxMaxima help.
Input lines shown below may be executed by selecting the input by clicking on
the input with the mouse and pressing Ctrl-Enter -- or Shift-Enter on some
implementations.
-----------------------------------------------------------------------------------------------------------------------
(%i1)
simp:false;
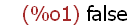
In Maxima, any expressions entered are simplified by default using a set of built-in
conventions for what is meant by "simplification" that for the most part result in
what would be expected. The simp flag is set to false to prevent simplification. In
this way input expressions are merely returned as entered. The following is a
easy example:
(%i2)
2*(3 + -4)/-2;
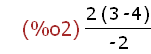
Simple operations of addition (+), multiplication(*), division (/) and subtraction (-) of
integers are involved with simple expessions. Note that Maxima does not require
parentheses between an operation and a negative integer -- (3 + -4). Now a more
complex arithmetic expression using a number raised to a power -- 2^2 which
means 2 squared, or 2 x 2:
(%i3)
2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13));
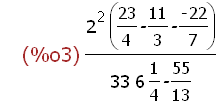
Again because the simp flag is false Maxima merely returns the entered expression.
When the expression is complex, this is a useful way to check that the entered
expression is what is intended. Maxima follows the conventional order of operations.
The results of these expressions may be had by setting the simp flag to true.
(%i4)
simp:true;
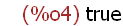
(%i5)
2*(3 + -4)/-2;

Maxima returns the result (simplification) of the expression -- in this case simply the
numeral for the integer 1.
(%i6)
2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13));
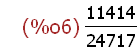
The result of this more complex expression is returned as an exact rational number
in the form of a fraction numeral. By default Maxima will return an exact result in the
simplest form -- an integer or rational number. The above fraction is returned in
lowest terms -- the numerator and denominator are relatively prime. To see this the
result is factored:
(%i7)
factor(%);
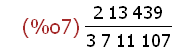
This result is the factored numerator and denominator. There are no common
prime factors. So this fraction has been simplified by Maxima and displayed in lowest
terms. The result of operations using rational numbers (fractions) and integers as
operands are always in the simplest possible form numerically. This means Maxima
takes care of details such as finding common factors, least common denominators,
and reduction to lowest terms for results in the form of fractions or integers. In this
sense Maxima always returns an exact numerical result in simplest terms. However,
a result may be obtained in the form of a decimal fraction that may or may not be
exact. This may be accomplished in several ways:
(%i8)
2.0^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13));
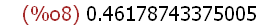
Use the decimal form of one of the numbers of the expression. This tells Maxima
that a decimal fraction result is desired. Here the leading integer 2 is changed to
2.0. The result is the decimal fraction shown with 14 digits of decimal precision.
This is not an exact result in this case. Also, in general the last digit may not be
reliable.
(%i9)
float(2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13)));
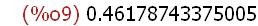
The float(expr) function returns a similar result.
(%i10)
2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13)), numer;
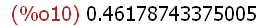
Using numer after the expression as in expr, numer also produces the same result
in decimal fraction form with the same precision. In case this is not enough precision,
Maxima provides a result with more precision in the form of a "big" decimal fraction
(a "big" floating point numeral) using the bfloat(expr) function:
(%i11)
(fpprec:16,bfloat(2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13))));
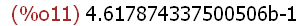
Using bfloat(expr) only squeezed out 2 extra digits of precision. However, big float
numerals are not limited to this precision. The default precision for bfloat is set by
a Maxima variable to 16 digits:
(%i12)
fpprec;
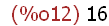
This number can be changed to any precision by assigning fpprec a larger value:
(%i13)
fpprec:32;

(%i14)
bfloat(2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13)));
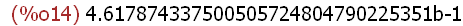
(%i15)
fpprec:48;

(%i16)
bfloat(2^2*((23/4)-(11/3)- (-22/7))/((33*6)*(1/4)-(55/13)));
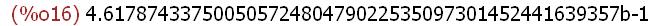
These results show that Maxima will display results in decimal form to the precision
required. This precision is usually limited by practical considerations and not by
Maxima. Also, big float numbers are displayed in the so-called scientific notation
format. The integer after the b in the numeral result displayed indicates
multiplication by 10 raised to this integer power -- here 1/10. Thus, it is clear that
fpprec sets the number of significant digits to be displayed in the result. The value
of fpprec does not affect results other than big float numerals. The last point to be
made is that results in decimal form may be rational approximations and not exact
depending on the expression involved. It is in this sense that in general we calculate
with approximations to real numbers and not exact numbers. Where a numeral is an
approximation to a real number it is due to truncation and rounding of significant
figures for whatever reason. Some irrational numbers that would otherwise result in
rational approximations in decimal form are symbolized exactly in Maxima results. All
algebraic irrationals -- roots of index n may be included in calculations and the results
will be symbolically exact.
(%i17)
sqrt(2); 3^(1/3); 5^(1/4);
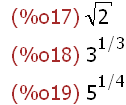
These results are exact. There is no error. Note that for roots other than the square
root of an expression, the result is expressed as a numeral to a rational exponent and
not by the so-called radical (or surd) notation (or sqrt(x) for Maxima). Some consider this
notation to be a nusiance. This default Maxima behavior may be changed by setting
the sqrtdispflag to false:
(%i20)
sqrtdispflag:false;
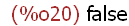
(%i21)
sqrt(2); 2^(1/2);
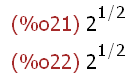
Thus the result of square root of an expression is displayed as the expression with a
rational exponent of 1/2. Also, this example shows that the square root of an expression
may be entered using the sqrt(expr) function or by an expression with an exponent that
is a common fraction -- 1/2. An example of this is worth considering because it illustrates
how Maxima follows rules for simplification:
(%i23) simp:false$
(%i24)
3^(5/2);

(%i25) simp:true$
(%i26)
3^(5/2);
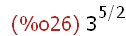
(%i27) sqrtdispflag:true$
(%i28)
3^(5/2);
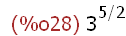
A decimal approximation as a result is obtained in one of the usual ways:
(%i29)
3^(5/2),numer;
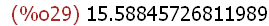
This result is known to be an approximation since the square root of 3 is irrational and
therefore has a non-repeating and non-terminating decimal representation. A result
with more precision may be obtained using fpprec and bfloat(expr) if required, but this
result is also not exact.
(%i30) sqrtdispflag:false$simp:false$
(%i32)
(105^(1/2)*(-42^(1/3))-(-36^(1/7)))*(-80^(1/5)/(20^(1/4)-17^(1/8)*30^(1/3)));
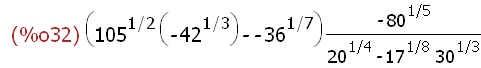
(%i33) simp:true$
(%i34)
(105^(1/2)*(-42^(1/3))-(-36^(1/7)))*(-80^(1/5)/(20^(1/4)-17^(1/8)*30^(1/3)));
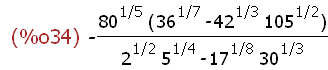
The result of this complex expression is symbolically exact and simplified, but not very
informative numerically. A numerical approximation is obtained as:
(%i35)
(105^(1/2)*(-42^(1/3))-(-36^(1/7)))*(-80^(1/5)/(20^(1/4)-17^(1/8)*30^(1/3))),numer;
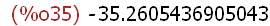
Maxima provides exact symbolic results for frequently used non-algebraic irrational
numbers -- so called transcendentals. Some examples are input and displayed below:
(%i36)
[%pi,%e,%phi];
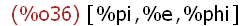
The above input creates another Maxima atom called a list object. It is used here
merely for convenience to contain the three "atoms" pi, e, and phi.
(%i37)
float([%pi,%e, %phi]);
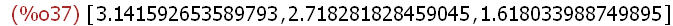
The elements of the list are displayed above in the form of decimal approximations for
these irrational numbers.
(%i38) simp:true$sqrtdispflag:true$
(%i40)
2^(1/2)*%e^(3*%pi);
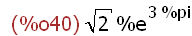
This is an exact symbolic result of an expression using algebraic and transcendental
irrational numbers.
(%i41)
2^(1/2)*%e^(3*%pi),numer;
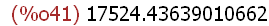
An approximation of the above expression in decimal form. There are other
expressions which display symbolic results that are not simplified automatically:
(%i42)
(1 + sqrt(2))^5;
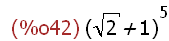
(%i43)
expand(%);
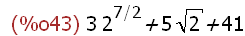
The first result is an exact symbolic expression, but it is not simplified in the sense
that the expression is not expanded numerically. Using expand(expr) function results
in an exact simplification. If an approximate numerical result is required this is
obtained in the usual way using the input expression in either form:
(%i44)
(1 + sqrt(2))^5,numer;
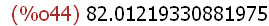
When using Maxima as a calculator, results may be retained in exact symbolic form to
any point at which a decimal result is required.
Maxima can manipulate very large numbers without approximation:
(%i45)
100!;

Note: wxMaxima will display this result with [98 digits] near the center not shown.
The resulting integer from the factorial expression 100! contains 158 digits. A number
this large is easily factored by Maxima:
(%i46)
factor(%);
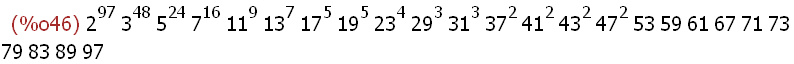
The % symbol used as an argument to the factor function above is a Maxima shortcut
for the last output.
The default wxMaxima display does not display all digits of large numbers (big integers
or bigfloat numbers). You can change to the ascii character display which displays all
digits using the input set_display(ascii). To return to the default display behavior enter
set_display(xml):
(%i47) set_display(ascii)$
(%i48)
100!;

(%i49) set_display(xml)$
Negative exponents behave as expected:
(%i50)
[2^(-1/2),3^(-3/2)];
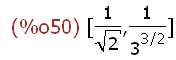
The results are in simplest symbolic form. Notice that Maxima does not consider
rationalizing the denominator as a simplification in a result.
Maxima may be used to determine if a number is prime or not and the next and
previous prime numbers with respect to any number.
(%i51)
[prev_prime(913),primep(913),next_prime(913)];
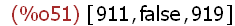
(%i52)
factor(913);
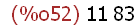
Thus, 913 is not prime (913=11 x 83). The previous prime number is 911 and the
next prime number is 919.
The greatest common factor (or divisor) of a number is given by the function gcd():
(%i53)
gcd(420,1176);
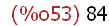
(%i54)
[factor(420),factor(1176)];
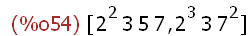
The least common multiple (lcm) can be obtained by dividing the product of the two
numbers by the gcd:
(%i55)
(1176*420)/gcd(420,1176);
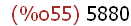
(%i56)
factor(%);
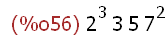
This factored form of the lcm makes sense. It contains the highest powers of all the
factors of 420 and 1176. Maxima does this simplification automatically if these
numbers are used in a fraction:
(%i57)
1176/420;

(%i58) simp:false$
(%i59)
(8/9)*(3/10);

(%i60) simp:true$
(%i61)
(8/9)*(3/10);

(%i62) simp:false$
(%i63)
(1/8)*((2/5)/(2/3));
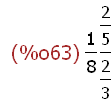
(%i64) simp:true$
(%i65)
(1/8)*((2/5)/(2/3));

(%i66)
(1/8)*((2/5)/(2/3)),numer;

The above input and results demonstrate simple but exact rational arithmetic with an
exact decimal result in the end. It is exact because 3/40 has a terminating decimal
fraction equivalent -- 75/1000. This is because 40=2x2x2x5 and these are all factors
of the base 10.
Maxima can return the results of logarithms. The log(x) function returns the natural
logarithm -- to the base e. It behaves as expected:
(%i67)
log(1);

(%i68)
log(%e);

(%i69)
log(%e*%pi);

(%i70)
log(%e*%pi),numer;
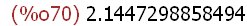
(%i71)
log(2);
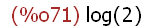
(%i72)
log(2),numer;
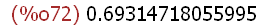
There is no built-in function for the logarithm to the base 10. However, this is easily
computed using the fact that this is equivalent to the log(x)/log(10):
(%i73)
log(2)/log(10);
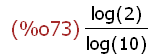
(%i74)
log(2)/log(10),numer;
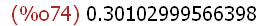
Results from previous output are automatically assigned an output label (e.g., %o74
above.) that may be referred to in any input expression:
(%i75)
%phi*%o74;
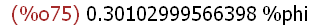
(%i76)
%phi*%o74,numer;
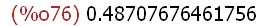
This practice can lead to undesired side effects in some situations, so this usage
should be avoided. There are other ways to do the same thing. A expression may
also be assigned a name in a way that emulates the memory registers of a calculator:
(%i77)
R0:(1/8)*((2/5)/(2/3)),numer;

(%i78)
R1:log(2)/log(10),numer;
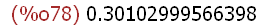
(%i79)
R0*R1;
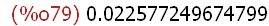
Exact symbolic and numerical results for the common trigonometric functions for
angles in radians are displayed from input as follows:
(%i80)
[sin(%pi/4), cos(%pi/3), tan(5*%pi/6)];
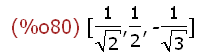
(%i81)
float([sin(%pi/4), cos(%pi/3), tan(5*%pi/6)]);
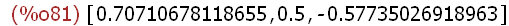
Degrees may be converted to radians by multiplying by pi/180. Thus 45 degrees is:
(%i82)
45*(%pi/180);

(%i83)
sin(%);

(%i84)
%,numer;
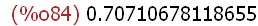
Maxima will calculate permutations and combinations. However, in order to do this a
Maxima package must be loaded using the load(functs) input where the argument
functs refers to a file named functs.mac. This brings into Maxima the functions
necessary to get results for permutations and combinations:
(%i85)
load(functs)$

(%i86)
permutation(10,5);
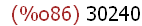
The number of permutations of 10 objects taken 5 at a time is 30240.
(%i87)
combination(12,5);

The number of combinations of 12 objects taken 5 at a time is 792.
A hand-held calculator may be more convenient for most purposes for getting
numerical results for expressions. They are portable and easy to use. Calculators
implementing the reverse Polish notation (RPN) handle complex chain calculations
quickly and quite well. However, if the expressions are moderately complex, it is
easy to make an error and difficult to know where the error occurred since
intermediate results are used up along the way. Maxima is an alternative for these
situations. You can check the accuracy of complex expressions and if the input is
correct, Maxima will return exact symbolic results without error and rational
approximations to the degree of precision required.
This "how-to" is a good introduction to the use of Maxima for simple calculations
and, if nothing else, provides important background understanding for using
Maxima in more sophisticated contexts.
(%i88) "Bye!"$