Differential und Integral

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

0.1 Handlinghilfen

0.2 Inhalt

1 Differentialrechnung
    1.1 Differential
    1.2 Nullstellen der Ableitung
    1.3 Zweite Ableitung
    1.4 Nullstellen numerisch
2 Integralrechnung
    2.1 Unbestimmtes Integral
    2.2 Bestimmtes Integral
    2.3 Uneigentliche Integrale

1 Differentialrechnung

1.1 Differential

--> f(x):=sin (x^2-1);

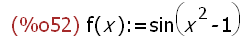
Für diese Funktion werden zwei Arten der Ableitungsdefinition vorgestellt.
Zuerst die "naheliegende":

--> foo(x) := diff(sin (x^2-1), x);

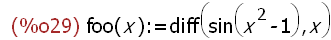
--> wxplot2d([foo(x),f(x)], [x,-5,5])$

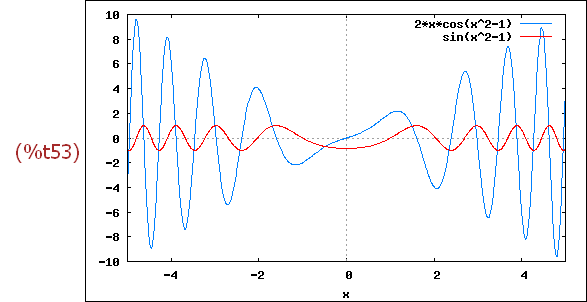
Das sieht eigentlich ganz gut aus, allerdings ist es nur eine
"symbolische" Angabe für foo. Man kann nun nicht ohne Weiteres für
x einen Wert einsetzen, das ergibt eine Fehlermeldung:

--> foo(3);

Das geht nicht, weil nun vesucht wird in den sinus schon 3 einzusetzen und dann
nach 3 abzuleiten. Das geht natürlich nicht.
Man muss das Auswerten des Term erzwingen, dass macht man mit doppelt geschriebenem
'' (nicht " !!!!! im Schriftbils der Eingabeschrift sieht das leider gleich aus)
Dieses tut der Plotbefehl intern noch nachträglich.

--> fs(x) := ''(diff(sin (x^2-1), x));

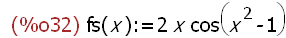
--> fs(3);

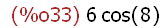
Wenn man, wie meist üblich die Ableitung, ihrerseits als Funktion untersuchen will
muss!!!! man so vorgehn.

1.2 Nullstellen der Ableitungen

--> solve(fs(x)=0,x);

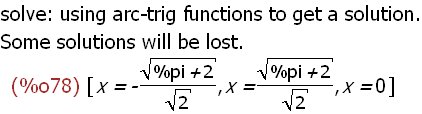
--> %,numer;

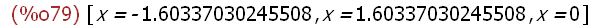
Zweite Ableitung

--> fss(x):=''(diff(fs(x),x));

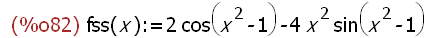
1.3 Zweite Ableitung

Die zweite Ableitung kann man bei der nicht empfohlenen Art
nicht als Ableitung der ersten Ableitung bilden.

--> foooo:=diff(foo(x),x);

1.4 Nullstellen mit numerischen Methoden

Nullstellen der zweiten Ableitung

--> solve(fss(x),x);

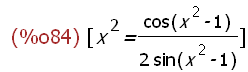
Dieses ist eine transzendente Gleichung, d.h. hier: x steht frei und in
transzendenten Funktionen. Solche Gleichungen sind meist nur numerisch lösbar.
Darum wird die zweite Ableitung erstmal gezeichnet, damit man sinnvolle Bereiche findet.

--> wxplot2d([x^2-cos(x^2-1)/(2*sin(x^2-1))], [x,-5,5],[y,-5,5])$

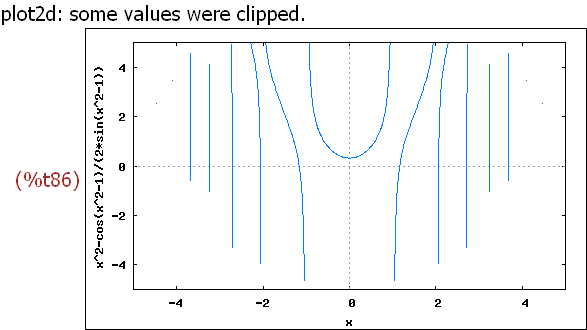
Bei x=1 ist sicher der Pol, rechts davon sieht man eine Nullstelle

--> find_root(x^2=cos(x^2-1)/(2*sin(x^2-1)),x,1.1,2);

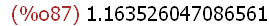
find_root arbeitet mit dem Sekantenverfahren, darum muss man ein Intervall angeben.
Es geht auch mit dem Newtonverfahren.

--> load (newton1);

--> newton (x^2-cos(x^2-1)/(2*sin(x^2-1)), x, 1.1, 1/100);

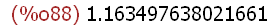
1.5 Regeln

--> diff(f(x)*g(x),x);

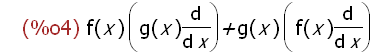
--> diff(f(x)/g(x),x);

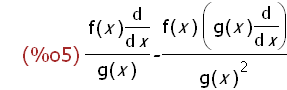
Die Kettenregel kann man nur an Beispielen zeigen.

--> f(x):=sin(x)^3;
diff(f(x),x);

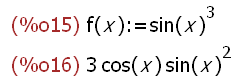
2 Intergralrechnung

2.1 Unbestimmte Integrale

--> integrate(x^2*sin(x^3),x);

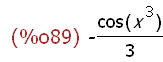
--> integrate(1/x,x);

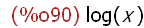
2.2 Bestimmte Integrale

--> wxplot2d([x^2,x^2*sin(x^3),-x^2], [x,-5,5])$

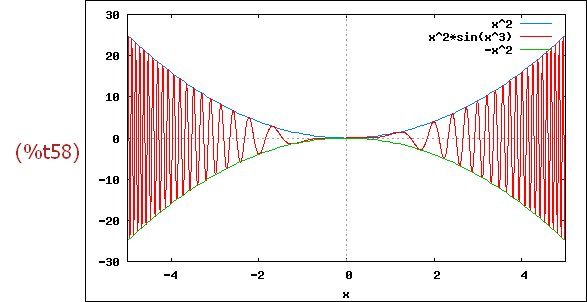
--> wxplot2d([x^2*sin(x^3)], [x,0,2])$

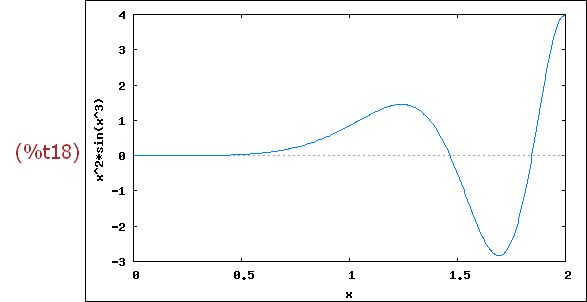
--> solve(sin(x^3)=0,x);

Mit Denken, erste Nullstelle rechts des Sinus

--> xd:(%pi)^(1/3);float(%);

Numerisch

--> x0:find_root(x^2*sin(x^3),x,1,1.6);

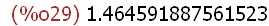
--> integrate(x^2*sin(x^3),x,0,x0);

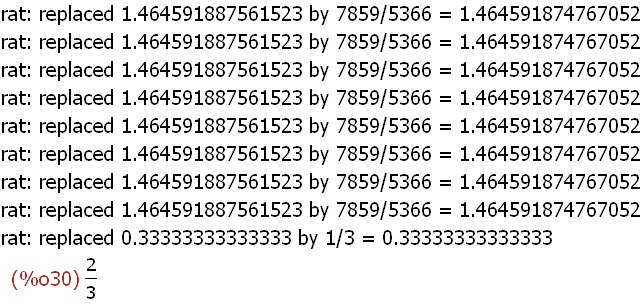
Man kann hier erkennen, wie Maxima versucht ein
exaktes Ergebnis zu erzeugen.

--> F(x):=''(integrate(x^2*sin(x^3),x));F(x);

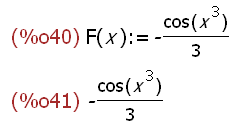
--> F(xd)-F(0);

Übrigens zufällig gefunden:
Kann man auch von Hand bestimmen.

--> xz:(%pi/2)^(1/3);

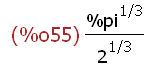
--> F(xz)-F(0);

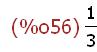
2.3 uneigentliche Integrale

--> integrate(1/x^2,x,1,inf);

--> makelist(integrate(1/x^2,x,1,c),c,1,30);

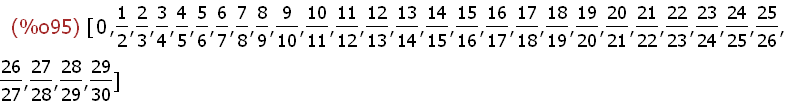
--> assume(c>2);

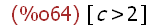
--> integrate(1/x^2,x,1,c);factor(%);

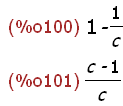
Achtung, auf die im Folgenden gestellten Fragen
muss man antworten, dann shift enter, damit es weitergeht.

--> integrate(1/x^a,x,1,c);factor(%);

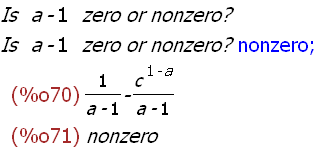
--> limit(1/(a-1)-c^(1-a)/(a-1),c,inf);

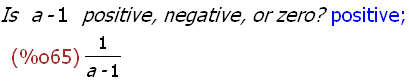
--> integrate(tan(x),x,0,%pi/2);