Folgen Reihen Grenzwerte

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

0.1 Handling

0.2 Inhalt

1 Folgen, explizit
    1.1 Folgen und ihre Darstellung
    1.2 Punktmatrix zeichnen
2 Reihen
    2.1 Summenfolgen
    2.2 Grenzwerte von Reihen
3 Grenzwerte von Funktionen
4 Stetigkeit von Funktionen
    4.1 Besondere Funktionen
    4.3 Stückweise definierte Funktionen

1 Folgen, explizit

1.1 Folgen und ihre Darstellung

Grenzwert(Term(n)),n,g) limit(term(n),n,g)
Welchen Grenzwert hat der Term, der von n abhängt,
wenn n gegen unendlich strebt?

--> Term(n):=float(n*sin(1/n))$

--> pkte:makelist([n,Term(n)],n,1,10);

--> limit(Term(n),n,infinity);

So kann man Punkte mit Folgenwerten erzeugen und den Grenzwert bestimmen.
Eine Zeichnung dazu:

--> wxplot2d(['discrete, pkte], [x,0,11])$

Man hätte auch Listen aus Stellen und Ordinaten einzeln machen können:

--> stellen:makelist(n,n,1,10)$
ordi:makelist(Term(n),n,1,10)$

Im Menu gibt es eine Möglichkeit, Plotten,Plot2D, Besondere Werte,
aber da werden zuviele Klammern gesetzt, wenn man stellen und ordi eingibt.

--> wxplot2d(['discrete, stellen, ordi], [x,0,11],[style,[lines,3,2]],
[gnuplot_preamble,"set grid;"])$

Welche Optionen man in wxMaxima bei wxplot2d für die Punkte setzen kann,
habe ich versucht herauszubekommen. Nicht gefunden.
Mehr Optionen hat man mit dem Originalbefehl aus Maxima.
Dann einsteht allerdings ein Extrafenster.

--> load(draw)$
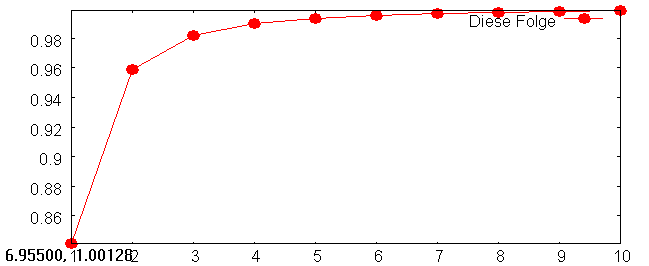
draw2d( key="Diese Folge",
        point_type =filled_circle, point_size = 1,color = red,
        points_joined = true,
        points(pkte));

Achtung!!! Hier geht es erst weiter, wenn man den gnuplot geschlossen hat.
Vorher kleiner machen, mit re-Maus, Optionen,Copy to clipboard Graph aufheben.
Dann hierin stellen. (An freie Stelle, nicht in Textzelle).

Figure 1:

Hier noch drei Folgen mit anderen Optionen.

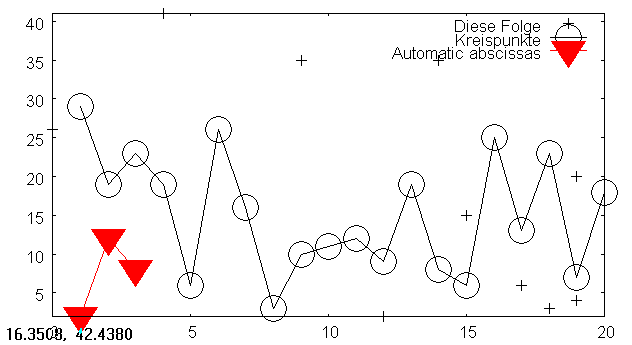
--> load(draw)$
draw2d(
        key = "Diese Folge",
        points(makelist([random(20),random(50)],k,1,10)),
        point_type = circle,
        point_size = 3,
        points_joined = true,
        key = "Kreispunkte",
        points(makelist(k,k,1,20),makelist(random(30),k,1,20)),
        point_type = filled_down_triangle,
        key = "Automatic abscissas",
  color = red,
        points([2,12,8]))$

Figure 2:

1.2 Zeichnen einer Punktmatrix

(%i1) z:10$ sp:15$

Definition von Arrays
Achtung: offenbar kann man Array nicht so einfach neu belegen.
Darum wird hier mit kill() das Array gelöscht,
damit ein echt neuer Durchlauf kommt.

(%i3) kill(t)$ t[i,j]:=random(2);
tm:genmatrix(t,z,sp);

Alle Einträge mit JA bzw. ok behalten ihre Koordinaten,
die jeweils anderen werden rechts abgelegt.

(%i6) kill(tmJA)$ tmJA[i,j]:=if tm[i,j]=1 then [i,j] else [z+1,1];
kill(tmok)$ tmok[i,j]:=if tm[i,j]=0then [i,j] else [z+1,2];

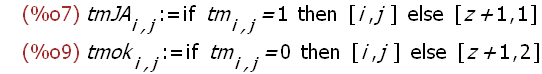
(%i10) tmJA[2,1];

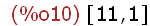
(%i11) load(draw)$

(%i12) liJA:[]$ for j from 1 thru sp do liJA:append(liJA,makelist(tmJA[i,j],i,1,z))$ liJA$
liok:[]$ for j from 1 thru sp do liok:append(liok,makelist(tmok[i,j],i,1,z))$ liok$

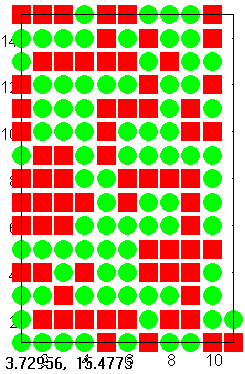
Es war etwas mühsam, die Punkte passend aufzubereiten.
Eine Matrix aus Punkten wurde nicht akzeptiert.
Nun ist eine Liste aus Punkten jeweils erzeugt.

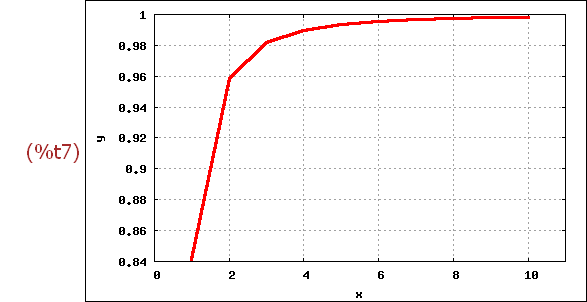
(%i20) pkt:gr2d(color=red, point_size=2,point_type=5, points(liJA),
              color=green, point_size=2,point_type=7, points(liok))$
draw(pkt)$

Figure 3:

2 Reihen

2.1 Summenfolgen

--> sum(i^2,i,1,n);

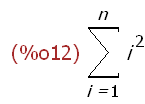
--> sum(i^2,i,1,10);

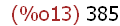
Summenfolge

--> makelist(sum(i^2,i,1,n),n,1,10);

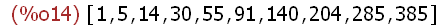
Geometrische Folge

--> a[i]:=ao*q^i;

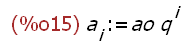
--> ao:2$ q:1/2$
makelist(a[i],i,1,10);

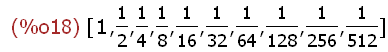
--> summenliste:makelist(sum(a[i],i,1,n),n,1,10);

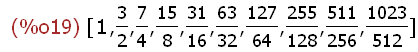
--> summenliste,numer;

2.2 Grenzwerte von Reihen

--> limit(sum(a[i],i,0,n),n,infinity);

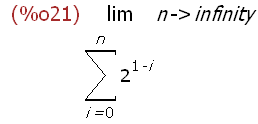
--> a[i];

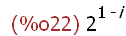
--> limit(a[i],i,infinity);

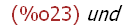
Die Ausgabe "und" heißt "undefined".

--> limit((1/4)^i,i,infinity);

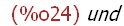
Das ist merkwürdig, denn der Grenzwert ist klar: 0

3 Grenzwerte von Funktionen

--> limit(sin(x)/x,x,0);

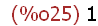
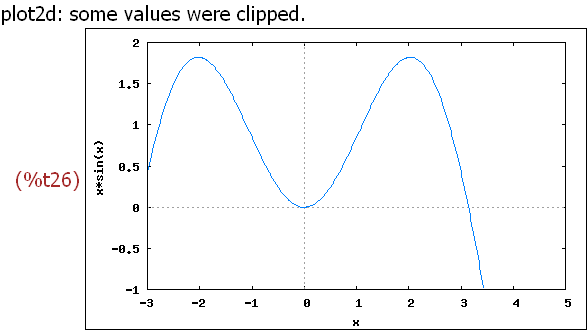
--> wxplot2d([x*sin(x)], [x,-3,5], [y,-1,2])$

--> log(%e);

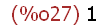
Der natüliche Logarithmus muss also log geschrieben werden, nicht ln.

--> limit(x*log(x),x,0);

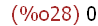
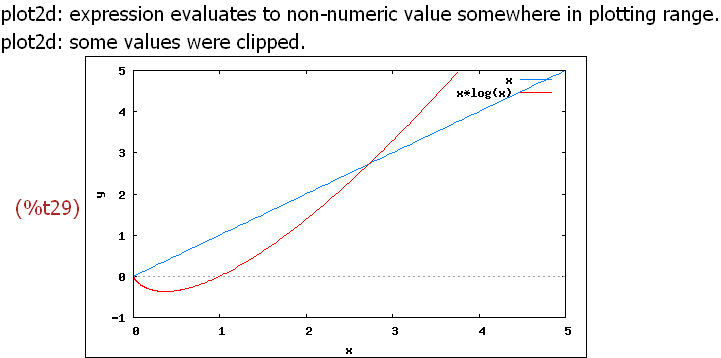
--> wxplot2d([x,x*log(x)], [x,0,5], [y,-1,5])$

--> limit(sin(x)/tan(x),x,0);

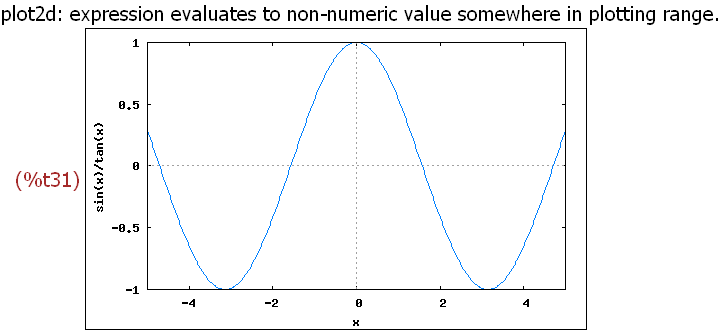
--> wxplot2d([sin(x)/tan(x)], [x,-5,5], [y,-1,1])$

4 Stetigkeit

4.1 Stetigkeit besonderer Funktionen

--> limit(sin(x)/tan(x),x,0);

--> wxplot2d([sin(x)/tan(x),cos(x)], [x,-5,5], [y,-1,1],
[style,[lines,3,1],[lines,1,2]])$

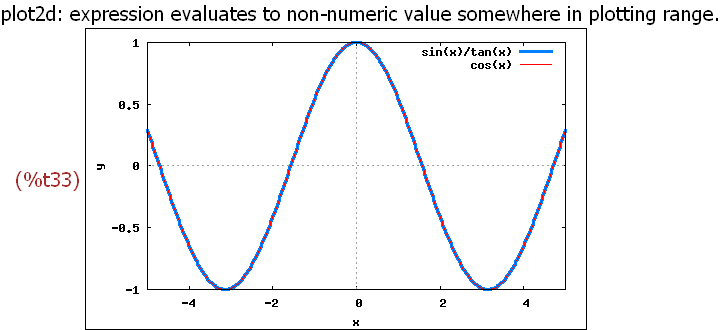
Damit ist der Kosinus die stetige Fortsetzung der ersten Funktion.

Einige Beispiele aus der Hilfe:

--> example(limit);

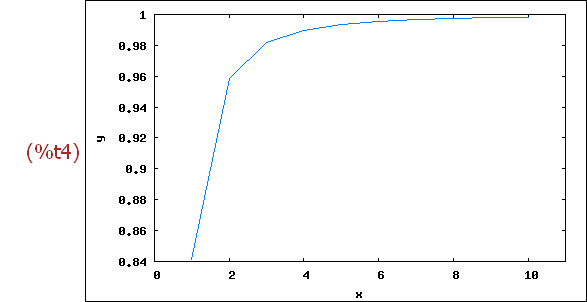
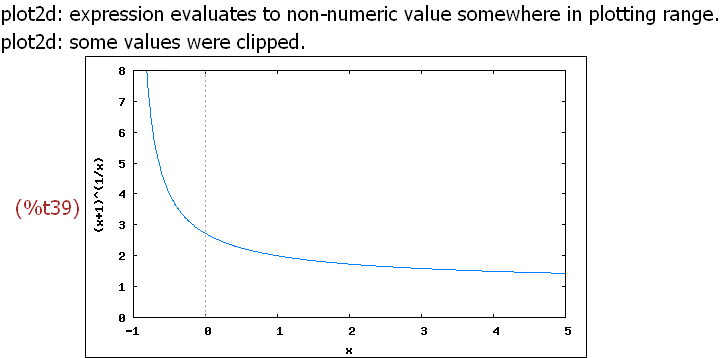
--> wxplot2d([(x+1)^(1/x)], [x,-1,5], [y,0,8])$

4.2 Stückweise definierte Funktionen

--> f(x):=if x<1 then x^2 else 1-x;

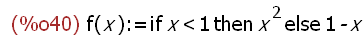
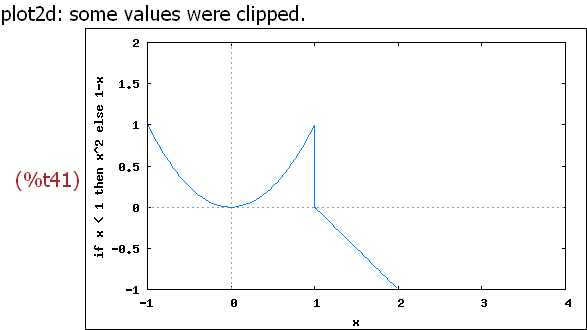
--> wxplot2d([f(x)], [x,-1,4], [y,-1,2])$

--> limit(f(x),x,1,minus);limit(f(x),x,1,plus);

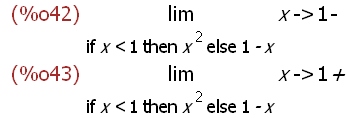
Funktioniert leider nicht

--> limit(x^2,x,1,minus);
limit(1-x,x,1,plus);

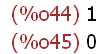
Also ist die Funktione unstetig in x=1.

--> limit(x^2,x,1,minus);
limit(2-x,x,1,plus);

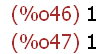
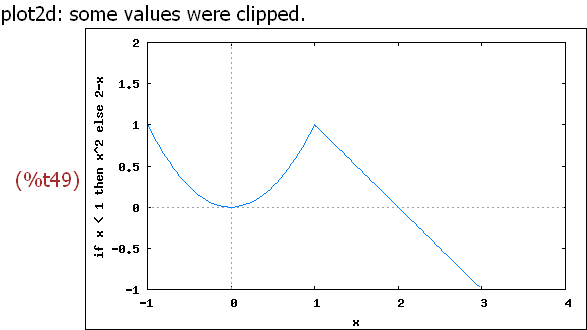
Also ist die Funktion g stetig in x=1.

--> g(x):=if x<1 then x^2 else 2-x;

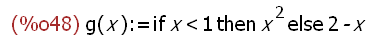
--> wxplot2d([g(x)], [x,-1,4], [y,-1,2])$