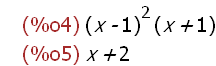Gebrochen rationale Funktionen

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Nov 2010

Hilfen zum Handling
Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.
Dazu Shift halten, dann werden auch alle Unterebenen aufgeklappt.

Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.

Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf,
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

Figure 1: Inhaltsverzeichnis

0.1 Definition

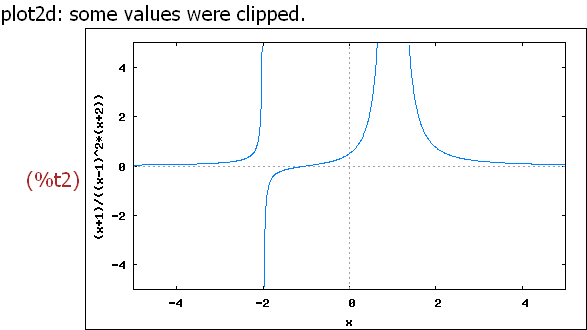
(%i6) h(x):=(x+1)/((x-1)^2*(x+2));

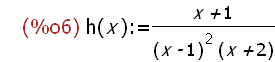
--> wxplot2d([h(x)], [x,-5,5],[y,-5,5])$

(%i7) num(h(x));denom(h(x));

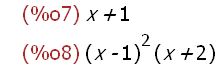
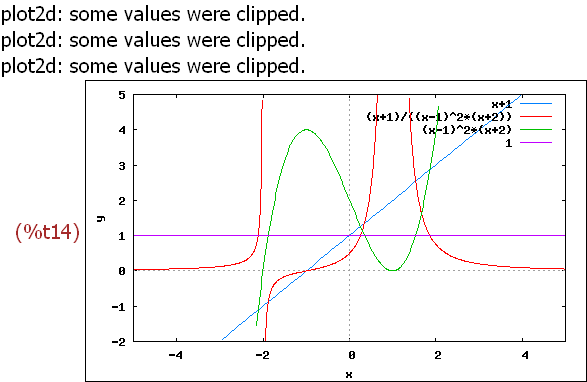
(%i14) wxplot2d([num(h(x)),h(x),denom(h(x)),1], [x,-5,5], [y,-2,5])$

1 Partialbruchzerlegung

1.1 Schnelle Lösung

--> hh(x):=partfrac((x+1)/((x-1)^2*(x+2)),x);hh(x);

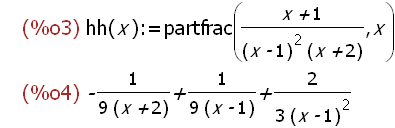
1.2 Elemente der von-Hand-Arbeit

--> glei:x+1=A*(x-1)*(x+2)+B*(x+2)+C*(x-1)^2;

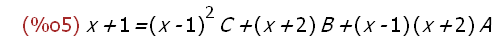
--> glei;

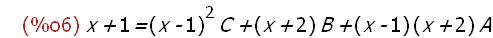
--> eins:subst(1,x,glei);
zwei:subst(-2,x,glei);
drei:subst(0,x,glei);

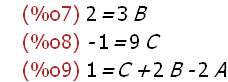
--> lo:solve([eins,zwei,drei],[A,B,C]);

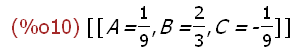
--> lo[1];

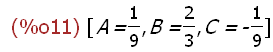
Einsetzung

--> subst(lo[1],glei);

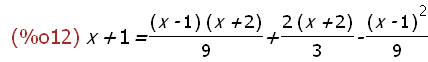
Probe

--> rhs(%);factor(%);

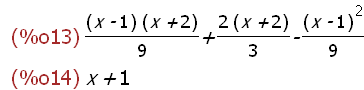
1.3 Koeffizientenvergleich

--> x+1=expand(A*(x-1)*(x+2)+B*(x+2)+C*(x-1)^2);

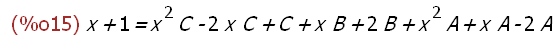
Mit Hinsehen eintragen

--> solve([0=C+A,1=-2*C+B+A,1=C+2*B-2*A],[A,B,C]);

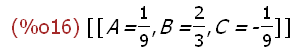
Dasselbe Ergebnis wie oben.

1.4 Zählergrad > Nennergrad

--> k(x):=(x+4)*(x-3)*(x-7)*(x+1)/((x-1)^2*(x+2));

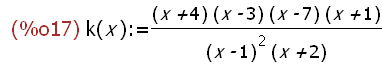
--> partfrac(k(x),x);

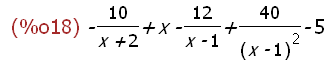
--> wxplot2d([k(x),x-5], [x,-15,15], [y,-15,15])$

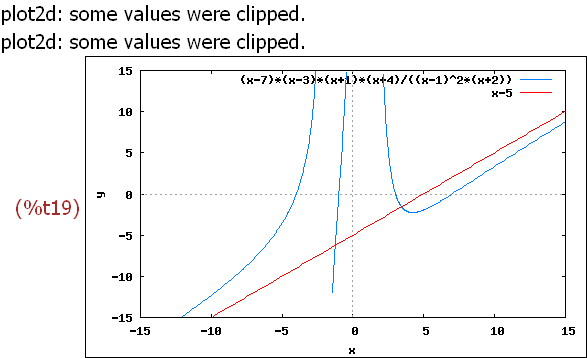
--> integrate(k(x), x);

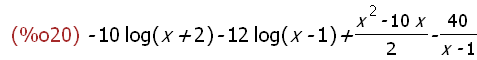
1.5 Weiteres Beispiel (vom Übersichtsblatt)

(%i2) f1s(x):=(x-1)^2*(x+1)/((x+2));

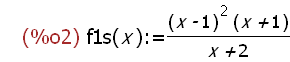
--> partfrac(f1s(x),x);

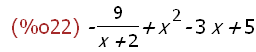
--> wxplot2d([x^2-3*x+5,f1s(x)], [x,-5,5], [y,-5,50])$

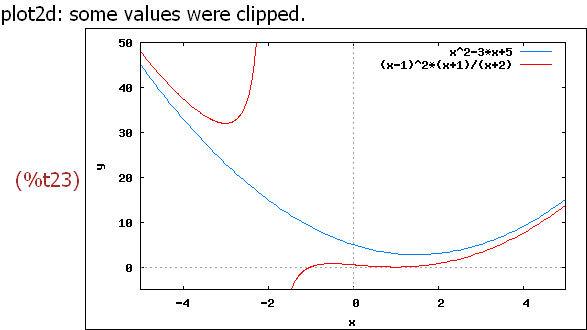
--> wxplot2d([x^2-3*x+5,f1s(x)], [x,-1.5,1.5],[y,-2,2])$

--> integrate(f1s(x), x, -1, 1);float(%);

(%i4) num(f1s(x));denom(f1s(x));