2d-Graphen systematisch dargestellt

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

0.1 Handling

0.2 Inhalt

Figure 1:

1 Graphen von einzelnen Funktionen (kartesisch)

Verwendung des Menus Plotten, Plot2d..., in Eingabemaske passend eintragen:

--> wxplot2d([sin(x)], [x,-5,5])$

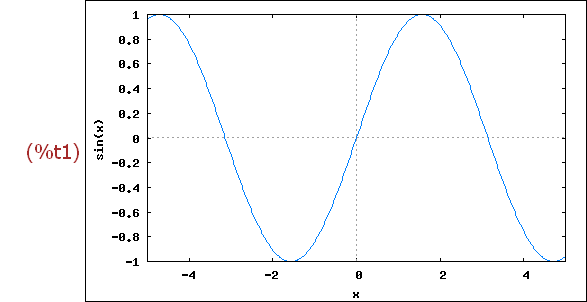
Funktion erst definieren:

--> f(x):=x^3-2*x^2+1;

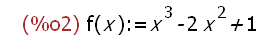
--> wxplot2d([f(x)], [x,-5,5])$

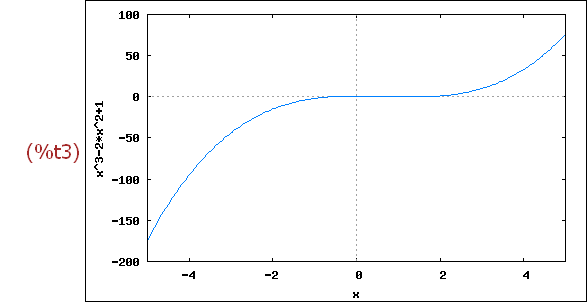
Ohne y-Angaben nimmt Maxima den gesamten Wertebereich zum x-Intervall.
Einen y-Bereich kann man in der Eingabemaske angeben oder von Hand in dem
blauen Text eintragen.

--> wxplot2d([f(x)], [x,-2,4], [y,-5,5])$

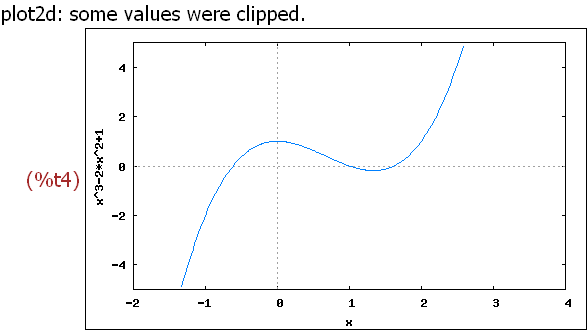
--> wxplot2d([f(x)], [x,-2,3],[y,-5,3],
 [gnuplot_preamble, "set grid;"])$

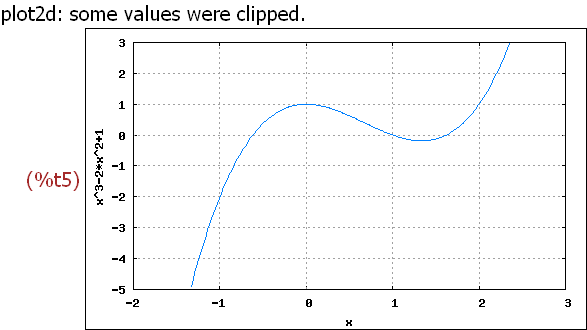
Bei Optionen in der Eingabemaske kann man die "Grids" wählen.
Zwischen die Anführungszeichen kann man noch mehr Optionen von Hand
schreiben, jede Option mit Semikolon.
Der Wunsch "Karopapier" zu haben, wie in Abschnitt 5 erfüllt.

2 Graphen mehrerer Funktionen

Am Einfachsten trägt man in die Listenklammern [] mit Komma getrennt
weitere Funktionsterme ein:

--> wxplot2d([x,f(x),(x-1)^2-4], [x,-2,3],[y,-5,3])$

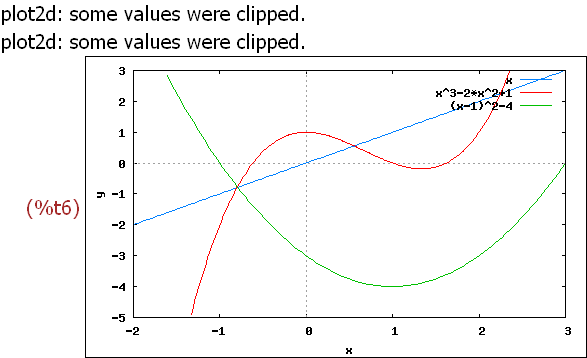
Man kann aber auch automatisch eine Liste erzeugen:

--> li: makelist(x^3-k*x^2+1,k,-2,7)$
wxplot2d(li, [x,-2,3],[y,-5,3])$

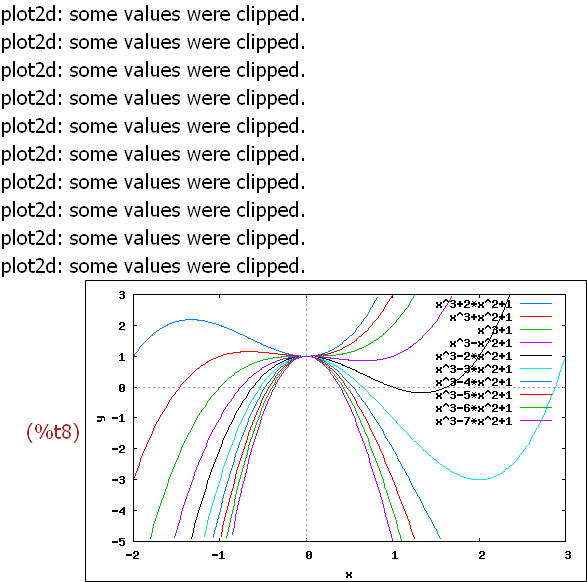
li ist dann schon eine Liste, darum fehlen im Plotbefehl die eckigen Klammern.
Die Meldungen: "plot2d: some values were clipped." würde ich gern unterdrücken,
ist mir bisher nicht gelungen.

Für Kurvenscharen ist es eleganter, eine Funktion passend zu definieren:

--> f[k](x):=x^3-k*x^2+1;

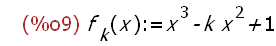
Dies entspricht der üblichen Art, k wird als Index aufgefasst.

--> li: makelist(f[k](x),k,-2,7);

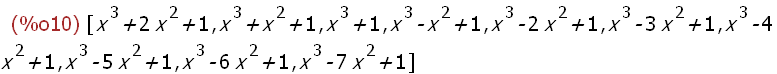
Das ist dieselbe Liste wie oben. Die vielen Funktionsterme unterdückt man
mit [legend,false]
Will man einen engeren Parameterabstand, so geht das so:

--> li2: makelist(f[i/4](x),i,-8,28)$
wxplot2d(li2, [x,-2,3],[y,-5,3],[legend, false])$

--> wxplot2d(li, [x,-2,5],[y,-10,7],[legend,false],[style,[lines,4,%n]])$

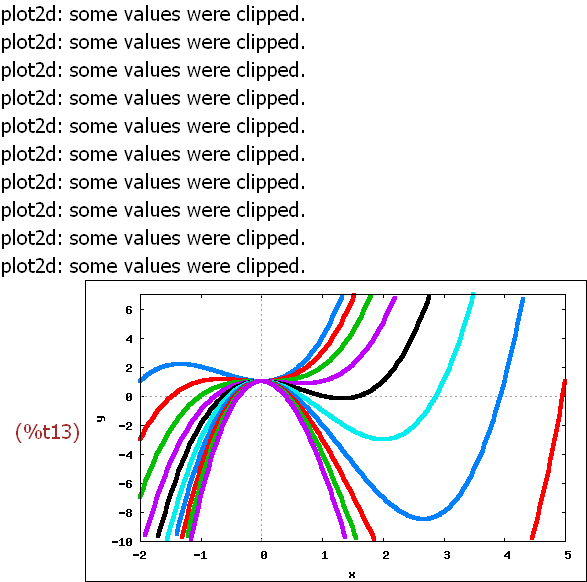
3 Animationen, Schieberegler

Eine moderne und wichtige Möglichkeit für die Lehre sind Schieberegler.

--> with_slider(k,makelist(i/4,i,-8,28),[k,f[k](x)],[x,-2,5],[y,-10,7]);

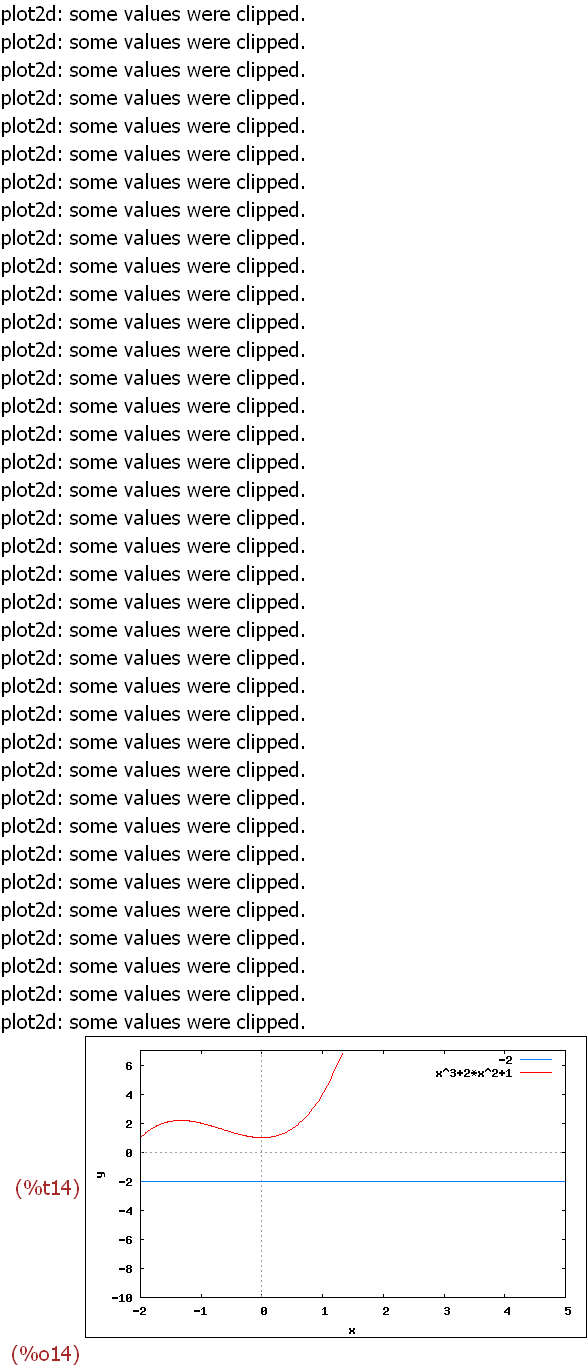
Oben in der Werkzeugleiste ist der Schieberegler. Markiere erst das Bild.
Hier ist k selbst auch eingetragen, damit die Legende besser ist.

4 Gestaltung von Farben, Dicken, Beschriftungen

Es gibt zwei Prinzipien für Optionen. Die wichtigsten sind in in wxMaxima
durch Listen [Name, Werte] verwirklicht.
Seltene Optionen kommen aus Maxima und stehen -wie oben "set grid;"- bei
[gnuplot_preambel, "opt1;opt2;.."]

--> wxplot2d([sin(x)], [x,-5,5],[xlabel,"Zeit"],[ylabel,"Amplitude"],
    [style,[lines,3,4]])$

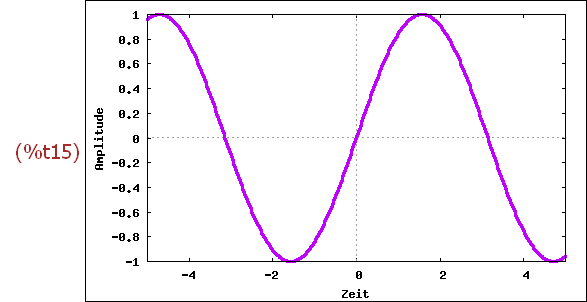
--> wxplot2d([0,sin(x),sin(x)+cos(x),sin(2*x)+cos(2*x),x ],
    [x,-5,5],[y,-2,2],[xlabel,"Zeit"],[ylabel,"Amplitude"],
    [style,[lines,5,3],[lines,2,4],[lines,3,2],[lines,4,1],
     [lines,1,5]]);

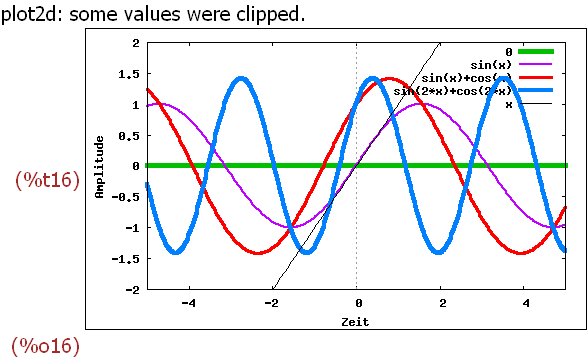
Hier wird der Linienstil in der Reihenfolge die zu zeichnenden Terme genannt.

--> wxplot2d([sin(x)+3], [x,-5,5])$

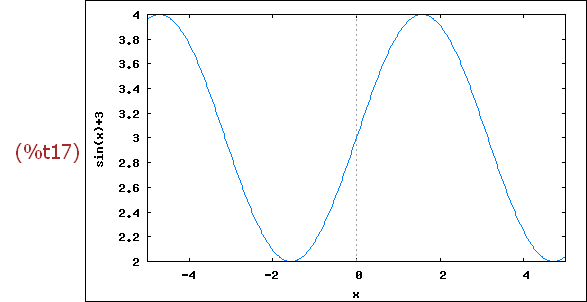
Wenn die x-Achse nicht im Wertebereich liegt, wird sie auch nicht gezeichnet.
Entweder man fügt noch 0 zum Zeichnen ein oder fordert den Wertebeich direkt.

--> wxplot2d([sin(x)+3], [x,-5,5],[y,0,4])$

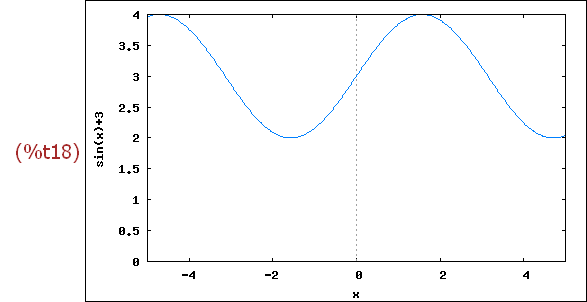
5 Seitenverhältnis, gleicher Maßstab

5.1 Vorschlag 2: Übliches Format, aber ymax1 selbst berechnen

--> (xmin:-1,xmax:2,ymin:-0.2,ymax:2)$
ymax1:ymin+0.6*(xmax-xmin) /*Nimm ymax1 für gleichen Maßstab*/;

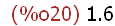
--> wxplot2d([1/2*x^2], [x,xmin,xmax], [y,ymin,ymax1])$

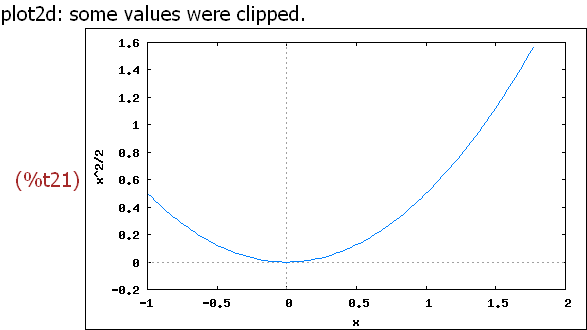
Die Idee ist: Die Fenster sind fast goldene Rechtecke,Höhe:Breite=0.6.
ymax1 ist so berechnet,
dass sich damit ein 0.6- Rechteck aus der Breite ergibt.
Darum sind nun die Einheiten rechts und und oben gleich lang.

Nun das fast-Karopapier mit dieser Darstellung.

--> wxplot2d([1/2*x^2], [x,xmin,xmax], [y,ymin,ymax1],
     [gnuplot_preamble, "set grid;"]);

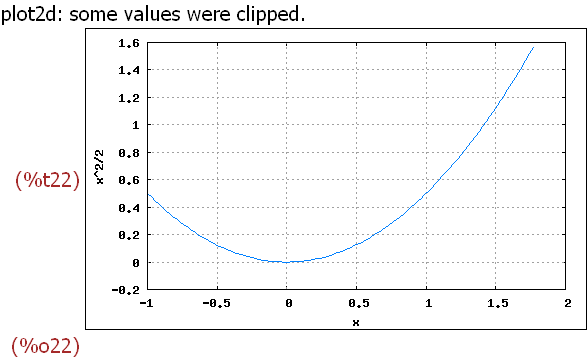
Oft wird das ja schon reichen für einen schulisch sinnvollen Eindruck.
Notfalls experimentiert man ein wenig mit anderen Grenzen.

5.2 Vorschlag 2: Grenzen wünschen, aber Format ändern

--> (xmin:-1,xmax:2,ymin:-0.2,ymax:3)$
(xpix:400, ypix:(ymax-ymin)/(xmax-xmin)*xpix);

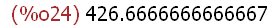
--> wxplot2d([1/2*x^2], [x,xmin,xmax], [y,ymin,ymax]),
    wxplot_size=[xpix,ypix];

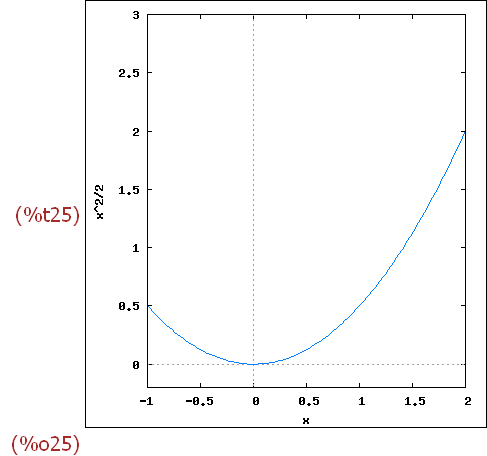
Achtung!!! der Befehl wxplot_size steht hinter!!! der Klammer-zu!!!

Nun das fast-Karopapier mit dieser Darstellung

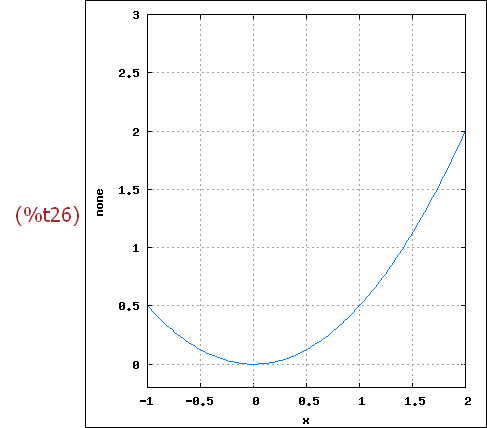
--> wxplot2d([1/2*x^2], [x,xmin,xmax], [y,ymin,ymax],[ylabel,none],
     [gnuplot_preamble, "set grid;"]),
    wxplot_size=[xpix,ypix]$

5.3 Vorschlag des Tutorials mit Option Ratio

--> (xmin:-2,xmax:4,ymin:-2,ymax:2)$
myratio:float((ymax-ymin)/(xmax-xmin));

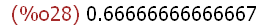
Diesen letzen Wert muss man nun leider von Hand übertragen nach ratio.

--> wxplot2d([sqrt(4-x^2),-sqrt(4-x^2),sqrt(4-(x-2)^2),-sqrt(4-(x-2)^2)],
    [x,xmin,xmax], [y,ymin,ymax],[legend, false],
[gnuplot_preamble, "set title 'Another way to make a circle
appear spherical'; set size ratio 0.66666666666667 ;"]);

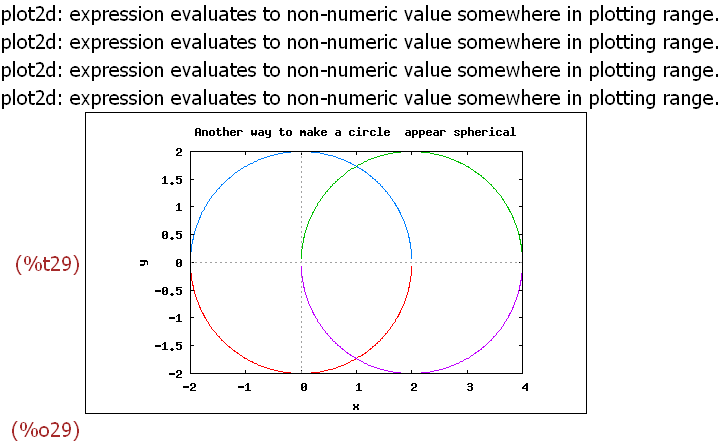
Nun also das versprochene Karopapier mit dieser Version.

--> (xmin:-2,xmax:4,ymin:-4,ymax:4)$
myratio:float((ymax-ymin)/(xmax-xmin));

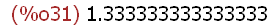
--> wxplot2d([f[-1](x),f[3](x),-(x-1)^2+2],
    [x,xmin,xmax], [y,ymin,ymax],[legend, false],
    [style,[lines,3]],
    [gnuplot_preamble,"set grid;
     set size ratio 1.333333333333333 ;"]);

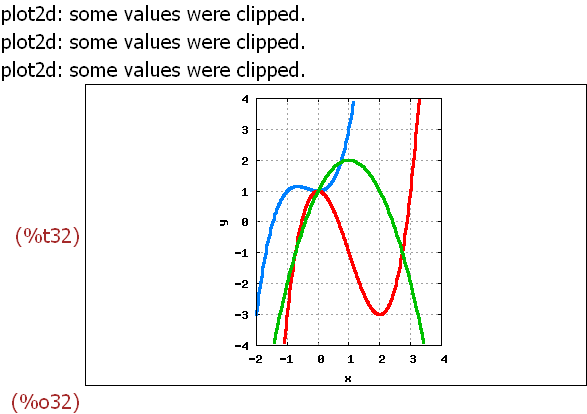
Diese Möglich keit bietet sich an, weil man wegen der Grids sowieso
gnuplot_preamble ansprechen muss.

über das wxMaxima zugrundeliedende Maxima kann man auf viel mehr
Möglichkeiten zugreifen. Es enstehen dann aber keine eingebetten Graphen,
sondern die erscheinen in einem Extrafenster.
Lies dazu die Datei "Erweiterte Zeichenmöglichkeiten".
Hier folgt nur ein Befehl als erster Eindruck.

--> load(draw)$

--> myplot:draw2d(xtics = 1/2,xtics_axis=true,grid=true,
       ytics = 1/2,ytics_axis=true,
       line_width=4, color="red",
             implicit(x^2+y^2=1,x,-5/3,5/3,y,-1,1) )$

Im entstandene Graphen-Fenster mit Options das Bild ins Clippboard nehemen,
dann schließen des Fensters, damit es hier weitergeht.

6 Stückweise definierte Funktionen

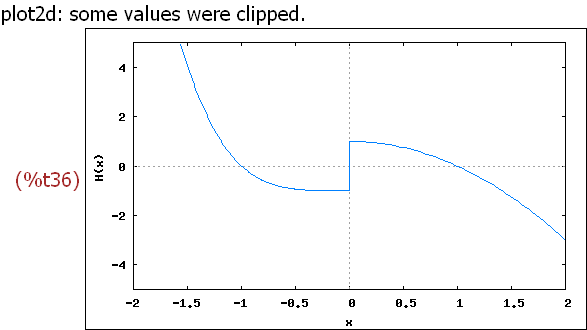
--> H(x) := if x < 0 then x^4 - 1 else 1 - x^2 $
wxplot2d([H(x)], [x,-2,2],[y,-5,5],[ylabel,"H(x)"])$

7 Parameterdarstellung

In der Eingabemaske für Plotten kann man bei "Besondere Werte" parametrisch
wählen.

--> wxplot2d([['parametric, t*cos(t), t*sin(t), [t, 0, 25],
     [nticks, 300]]], [x,-25,25]),wxplot_size=[400,400]$

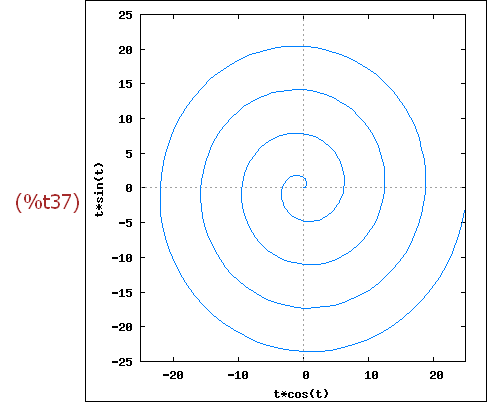
Der Befehl wxplot_size=[400,400] ist hier nicht berechnet sondern
einfach so gesetzt, da in y-Richtung auch 50 Einheiten dargestellt waren.

8 Polarkoordinaten

In der Eingabemaske von Ploten kann unten bei Otionen
"polar" gewähltwerden.
Die folgende Darstellung hat aber den Fehler, dass keine
zwei Runden gezeichnet werden.

--> wxplot2d([ph], [ph,0,4*%pi],[y,-13,10],
 [gnuplot_preamble, "set polar; set zeroaxis;"])$

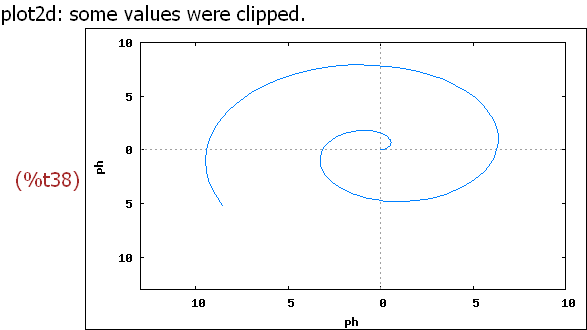
Also empfiehlt es sich, diese Möglichkeit zu meiden und
stattdessen Polarkoordinaten parametrisch zu erzeugen.
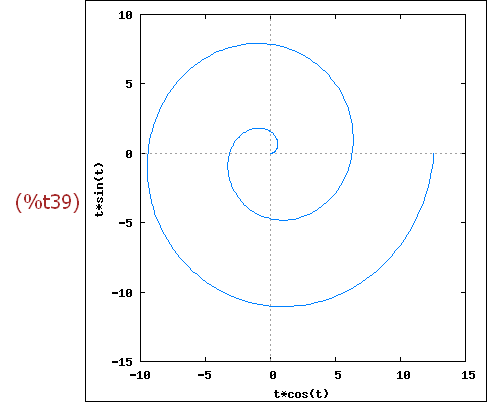
Dieselbe Archimedische Pirale also:

--> wxplot2d([['parametric, t*cos(t), t*sin(t), [t, 0, 4*%pi],
     [nticks, 300]]],
     [x,-10,15],[y,-15,10]),wxplot_size=[400,400]$

9 Implizite Darstellung

--> load(implicit_plot)$

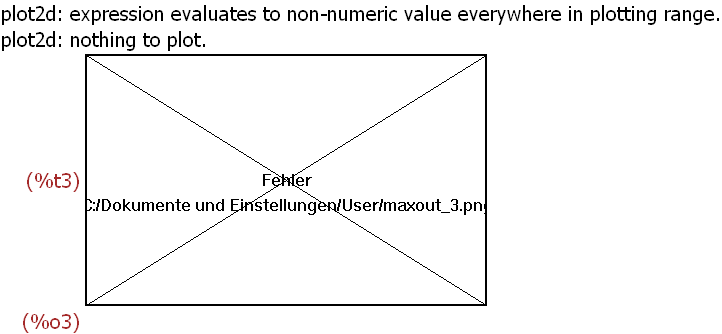
Dies ist mir hier noch nicht gelungen. In der Datei
"erweiterte Zeichenmöglichkeiten" habe ich eine Lösung mit gnuplot.

(%i3) wxplot2d([['implicit, x^2=y^3-3*y+1,[x,-4,4],[y,-4,4],
   [nticks, 300]]],
  [x,-4,4] );

10 Graphen verschiedener Typen in einem Bild.

Als Erstes steht in dem Befehl wxplot2d([...] die Liste der zu
zeichnenden Objekte. Diese können von unterschiedlichem Typ sein.

--> p(x):=-(x-3*%pi)^2/%pi+%pi;

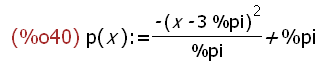
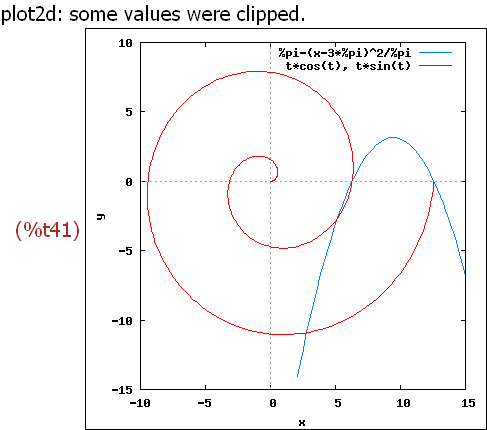
Hier also zwei Objekte: eine Parabel und eine Parametrische Kurve.

--> wxplot2d([p(x),['parametric, t*cos(t), t*sin(t), [t, 0, 4*%pi],
     [nticks, 300]]],
     [x,-10,15],[y,-15,10]),wxplot_size=[400,400]$

--> s;