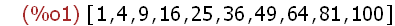
Listen, Folgen, Mengen

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.

Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.

Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf,
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

wxMaxima ist über Maxima und Macsyma ein Lisp-Abkömmling.
Die Sprache Lisp ist Listenorientiert. Daher spielt auch bei
wxMaxima das Listenkonzept eine große Rolle.

1 Listen

1.1 Listen erzeugen

Über das Menu Algebra sind die Listenbefehle verfügbar.

(%i1) makelist(k^2, k, 1, 10);

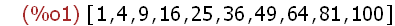
Erstellung von Wertetabellen zu vorgegebenen Stellen

(%i2) makelist(x^3-x^2+1,x,[-1,0,2,3,7]);

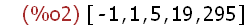
Erstellung der Punktkoordinaten auf einem Graphen an
gewünschten Stellen.

(%i3) punkte: makelist([x,x^3-x^2+1],x,[-1,0,2,3,7]);

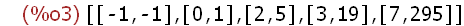
Listen bestehen aus mit Komma getrennten Objekten in eckigen Klammern.
Man kann sie einfach von Hand eingeben.
Mit : wird der Variablen liste1 diese Liste zugewiesen.

(%i4) liste1:["eins", 2, "tree", "IV"];

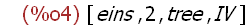
Die Objekte können auch untereinander verschieden sein.
Die Reihenfolge ist bei Listen wesentlich.

(%i5) liste2: [1,3,5,3,3,5];

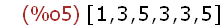
Erzeugung von Variablen und Gleichungen mit diesen

(%i6) makelist(concat(a,i)=i^2,i,[2,4,3,6]);

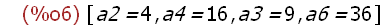
Achtung!! Das sind keine Zuweisungen.

(%i7) create_list(x^i,i,[1,3,7]);

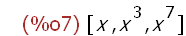
Erzeugen aller Paarungen aus zwei Listen

(%i8) create_list([i,j],i,[a,b],j,[e,f,h]);

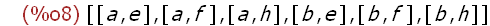
Erzeugen einer "Dreiecksform"

(%i9) create_list([i,j],i,[1,2,3],j,i,3);

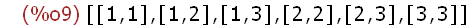
(%i10) create_list([i,j],i,[1,2,3],j,1,i);

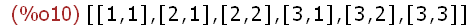
(%i11) create_list([i,j],i,[1,2,3],j,[1,i]);

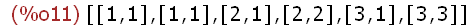
1.2 Listen zusammenfügen

Aneinanderhängen von Listen

(%i12) append(liste1,liste2);

Reißverschluss-Verbindung,
die letzten Elemente der längeren Liste werden ignoriert

(%i13) join(liste1,liste2);

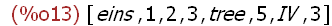
Die folgenden Anwendungen von append funktionieren, da die Operatoren
+ , * usw. intern Listen sind.

(%i14) append(a^2-b^2,x+y);

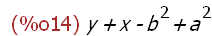
(%i15) append(a^2*b^2,x*y);

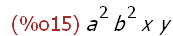
1.3 Listenoperationen

Liste umdrehen

(%i16) reverse(liste1);

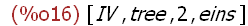
(%i17) reverse(x^y);

Löschen eines Elements und seiner Kopien

(%i18) delete("tree",liste1);

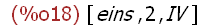
(%i19) liste2;

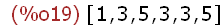
(%i20) delete(3, liste2);

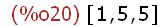
alle 3-Vorkommen sind gelöscht

Achtung!! die Liste bleibt selbst unangetastet. Die kurze Liste muss man
einer Variablen zuweisen. Will mann liste2 wirklich kürzer haben
so muss man liste2:delete(3, liste2); schreiben.

(%i21) liste2;

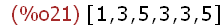
(%i22) delete (sin(x), x + sin(x) + y);

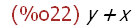
Einfügen eines Elementes
vorn, hinten

(%i23) cons("null",liste1);

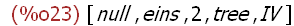
(%i24) liste3:endcons("V",liste1);

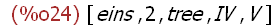
Herausgreifen eines Elementes, die Liste selbst bleibt bestehen:
vorn, Platz n, hinten, (Vorsicht bei Termen!)

(%i25) first(liste1); first(x+y);

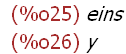
(%i27) liste1[3];

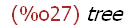
(%i28) last(liste1);

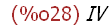
Wegwerfen der ersten n, bzw. der letzten n Elemente (mit -n)

(%i29) liste3;

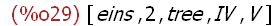
(%i30) rest(liste3,2);rest(liste3,-2);

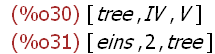
Herausgreifen und Wegwerfen des n-ten Elementes,
hier des 4. Elementes aus liste3

(%i32) delete(liste3[4],liste3);

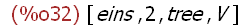
1.4 Untersuchung von Listen

Anzahl der Listenelemente

(%i33) length(liste1);

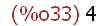
Prüfung, ob es sich um eine Liste handelt

(%i34) listp(liste1);

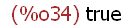
(%i35) listp(y+x);

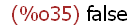
Prüfen, ob ein Element drin ist.

(%i36) member("tree",liste3);member(2,liste1);

Eliminierung der Doubletten

(%i38) unique(liste2);

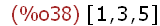
1.5 Anwendung von Funktion auf Listen

Viele Funktionen kann man einfach so auf Listen anwenden.
Die Funktionen heißen dann listenfähig oder listable

(%i39) sin(liste2);

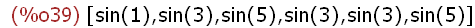
(%i40) f(x):=x^3-7;

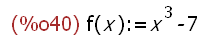
(%i41) f(liste1);f(liste2);

2 Folgen

In MuPad entstehen Folgen aus Listen durch Weglassen der
eckigen Klammern. Dafür habe ich in Maxima noch keinen Befehl gefunden.
Offenbar kann man mit Komma getrennte Befehle mit runden Klammern
zusammenfassen. a,b unc c haben dann die passenden Werte, wie man sieht.

(%i43) (a:3,b:4,c:5);[a,b,c];

Löschen von Variablenbelegungen, Menu Maxima Variable löschen

(%i45) remvalue(a,b,c);

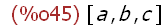
3 Mengen

3.1 Definition von Mengen

Mengen werden mit geschweiften Klammern geschrieben.
Die Reihenfolge der Elemente ist nict relevant.
Es kann keine doppelten Elemente geben.

(%i46) A:{2,6,4,2,2};B:liste:[5,5,6,6];R:set(s,rs,r,s);

Mengen aus Listen machen:

(%i49) B:setify(liste);

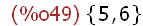
3.2 Mengenoperationen

(%i50) Ver:union(A,B);

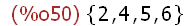
(%i51) Durch:intersection(A,B);

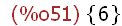
(%i52) setdifference(A,B);
setdifference(B,A);
setdifference(A,A);

Vereinigung, Durchschnitt und Differenzmengen wie üblich.

(%i55) Om:setify(makelist(i,i,1,20));

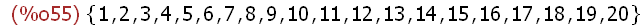
(%i100) complement(U,AA):=setdifference(U,AA)$

(%i101) complement(Om,A);

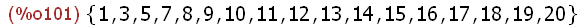
Für des Komplement braucht man natürlich eine Bezugsmenge.

(%i103) P:powerset(A);

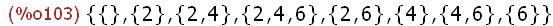
Die Potenzmenge ist die Menge aller Teilmengen

(%i58) cardinality(A);cardinality(R);

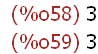
(%i104) cardinality(P);

Die Potenzmenge von A hat 2^n Elemente, wenn A n Elemente hat.

(%i109) S:{1,2,3,4,5,6,7,8,9,10}$
subset(S,evenp);subset(S,oddp);

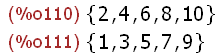
Hier wird aus S mit der "gerade-Frage" und der "ungerade-Frage" ausgewählt.

(%i60) onetoone(AA,BB):=is(cardinality(''AA)=cardinality(''BB))$
onetoone(Durch,Ver);onetoone(A,R);

Lies one to one, also eine ein-zu-ein-Zuordnung ist möglich.

(%i63) 'subsetp(Durch,Ver);
subsetp(Durch,Ver);

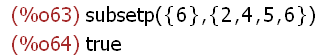
Das führende Hochkomma unterdrückt die Auswertung.
p steht für "proof", also Püfung.
Damit ist die eine Prüfung auf "Ist Untermenge von"

(%i65) S:{1,3,4,5,6};D:{11,2,20};A;B;

(%i69) disjointp(S,D);
disjointp(S,''A);disjointp(''A,''B);

Dies ist Prüfung auf "Sind die Mengen disjunkt"
Dies stimmt in Maxima aunh für die leere Menge, wie es die Theorie fordert

(%i72) subsetp(S,{});
subsetp({},S);
subsetp(S,S);
subsetp({},{});

(%i105) divisors(1024);divisors(941);

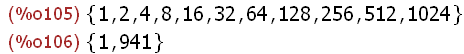
Since the only divisors of 941 are itself and 1, the result above indicates that 941 is a
prime number. Another method uses the makeset(expr,x,s) function.

(%i107) S:{[1,2],[3,4],[5,6],[7,8]}$
makeset([n/d],[n,d],S);

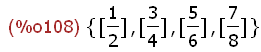
3.3 Hinzufügen zu und Wegnehmen aus Mengen

(%i76) adjoin(20,A);

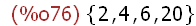
(%i77) delete(2,A);

Wie immer: A selbst wird nicht angetastet, man müsste sonst A: davorschreiben.
Bei Listen ist der Bezug auf eine Stellung nicht sinnvoll.

(%i78) A[3];

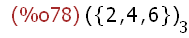
(%i79) member(6,A);member(7,A);

3.4 Bespiele für Mengen mit Eigenschaften

(%i81) Z:{1,4,5,6,3,9,11};

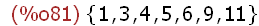
(%i82) evens(S):=(E:{}, for e in S do (if evenp(e) then E:adjoin(e,E)),E)$
odds(S):=(O:{}, for e in S do (if oddp(e) then O:adjoin(e,O)),O)$
evens(Z);odds(Z);

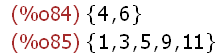
3.5 Anwenden von Funktionen auf Mengen

Die Funktion rat (von rational) ist in anderen Sprachen: simplify
also: rationale Vereinfachung von Termen

(%i86) rat(3+r+4+r);

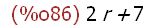
(%i87) map(rat,{2*r+7,3+r+4+r,2*(r+7/2)});

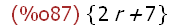
Eben war es eine Menge, gleiche Elemente werden identifiziert,
unten ist eine Liste, jedes Element wird vereinfacht, bleibt aber
an seinem Platz.

(%i88) map(rat,[2*r+7,3+r+4+r,2*(r+7/2)]);

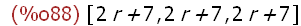
Das war z.B. ratiomale Umformungen von Termen,
also eine Termumformungsprüfung

Etliche Listenoperationen funktionieren auch auf Mengen.
Weitere Funktionen sind in der Hilfe bei Inhalt->set