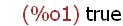
Minimal-Maxima-Verstehen
Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010
Dieses ist nicht in Deusch adaptiert, da die Erkenntnisse in die
in Deutsch entwickelten thematischen Dateien eingebaut worden sind.
(Zudem war mir eine nette Datei abgestürzt)
0.1 Der Autor und seine Daten
Minimal Maxima
Abstract
This Maxima session is based on the Minimal Maxima paper:
(http://maxima.sourceforge.net/docs/tutorial/en/minimal-maxima.pdf)
written by Robert Dodier dated September 10, 2005. Much of the what appears
below is directly quoted from this paper. However, there is also much that has
been edited and this may not be reflected as such where this occurs. Please
refer to the original paper available at the URL above. Where there exists a
segment of text in the form of a note, as in [Note: ...], this is intended to
emphasize that the information was added for the purpose of this tutorial and
that this text is not contained in the original paper. The absence of this notation
does not mean that the text involved is directly quoted as there are numerous
changes and additions. Still, any credit goes to the author of the original paper
and any defects must be mine.
Notes:
This session is not comprehensive or exhaustive, however some of the basic
Maxima functions and features are demonstrated. Please note that there may
be alternative ways to form the Maxima statements of this session. Refer
to the Maxima documentation and the wxMaxima help.
Input lines shown below may be executed by selecting the input by clicking on
the input with the mouse and pressing Shift-Enter -- or Ctrl-Enter on some
implementations.
Table of Contents
1 Introduction
2 What is Maxima?
3 Expressions
3.1 Mathematical Expressions
3.2 Object Expressions
3.3 Programming Constructs
3.4 Examples of Maxima Expressions
3.5 Useful Maxima Functions
3.6 Expression Construction
4 Evaluation
4.1 Modifications of Evaluations
4.2 Default Evaluation
4.3 Evaluation of Arguments
4.4 Callable Functions
4.5 Automatically Quoted Arguments
4.6 Preventing Evaluation
4.7 Extra Evaluation
4.8 Arguments to apply()
4.9 Arguments to define()
5 Simplification
5.1 Examples of Maxima Simplification
5.2 Exceptions to Maxima Simplification
6 Special Purpose Functions
6.1 apply()
6.2 map()
6.3 lambda()
7 Built-in object types
7.1 Lists
7.2 Matrices
7.3 Sets
8 Maxima Programming
9 Summary
Note: Click on the black square box icon at the upper left of
each section title below to expand (open) that section.
The square will now be white. Click it again to close
sections as desired.
1 Introduction
Trying to learn to use Maxima by reading the documentation can be an experience
of frustration. On the other hand, trying to learn how Maxima works by trial and
error can be as frustrating, if not more. How Maxima works makes a lot of sense
once you get used to the neighborhood. This tutorial is like a trip around the
neighborhood of Maxima in which there is no particular destination in mind. The
goal is merely to stop here and there and get familiar with the main features of
the neighborhood while avoiding dead ends and alleys by staying on the main
streets in order to get a feel for what the environment of the Maxima
neighborhood has to offer. This is important to understand at the start since
a certain amount of patience and perseverance is required in this sort of
effort. At the end you will turn up again where you started, but with a new
appreciation for working in the Maxima neighborhood.
One of the benefits of using Maxima appears to be that it helps you understand
mathematics either better or (if not) at least in a new way that provides a
different perspective for mathematical concepts. There are those who believe
that using computer hardware and software, a calculator, a slide rule, an abacus,
or other such aids with respect to mathematical understanding is detrimental in
some way or another. This appears to be old wine in new bottles in the form
of the "algorists" versus the "abacists."
The important point is understanding and then to be able to do something with
that understanding. It is not nearly as important that this understanding and the
applications of the understanding comes in this form or that form. While it is true
that there is no substitute for understanding the essentials, it is also true that
one should not have to drag them around like weights on chains forever. Anything
that helps you understand a subject or helps in the applications of that subject
may be worth the time and effort involved. It is only when these are used as a
substitute for understanding or to compensate for deficiencies in essential skills
that undesired side effects may occur.
2 What is Maxima?
Maxima is a system for working with expressions, such as x+y, sin(a+b*pi), and
uv - vu. Maxima is not much worried about the meaning of an expression.
Whether an expression is meaningful is for the user to decide. Sometimes you
want to assign values to the names and evaluate the expression. Maxima is
happy to do that. But Maxima is also happy to postpone assignment of specific
values; you might carry out several manipulations of an expression, and only
later (or never) assign numerical values to names.
[Note: Maxima belongs to a category of mathematics software known as computer
algebra systems -- or CAS for short. By categorizing Maxima as such it is
meant to imply that it is a tool primarily for the manipulation of mathematical
objects as symbols rather than merely as numerical objects -- numbers. Now
since it is never the case that humans deal directly with numbers (only symbols
for numbers called numerals) an argument can be made that the distinction
between numerical and non-numerical mathematical symbology is somewhat
arbitrary. In fact, Maxima has the capability of manipulating numerical
symbology quite well, but it is not limited strictly to manipulations of that
kind. Thus Maxima may be applied to manipulations of a much broader spectrum
of mathematical symbology. Other software exists with the intentionally
specialized purpose of manipulating numerical data and displaying results as
numerical data -- that is, performing calculations. For those questions that are
limited to numerical data and results, this category of software is adequate, and
may be more appropriate depending on the nature of the task at hand. Examples
of open-source software of this category are Euler Math Toolbox, R, and Octave.]
[Note: Click anywhere in each of the blue text input fields below and press
Shift-Enter (or Ctrl-Enter). The first command below sets a Maxima flag that
displays a dot in wxMaxima (or an asterisk in Maxima) denoting the operation of
multiplication. If this flag is set to stardisp:false (the default) a blank space is used
instead and this can be distracting in some contexts.]
(%i1)
stardisp:true;
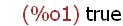
Let's see some Maxima examples.
1. What is the expression for the volume of a sphere.
(%i2)
V:4/3 * %pi * r^3;
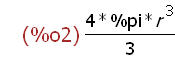
In this example, the ouput expression is the value assigned to the name V.
Names in Maxima are also termed identifiers. The value of the name
r (for radius) is "itself" at this point -- that is, r is r. It may be assigned a
specific numerical value instead. Note that the number pi is entered using
the Maxima special characters %pi.
[Note: If using wxMaxima with the preferences set to use a Greek font with the
SPlonic font installed on your system, the constant pi will appear as the Greek
letter for pi instead of as %pi.]
2. Assign the value of 10 to the radius r.
(%i3)
r:10;
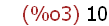
The way to assign a specific value to a name is to use a colon character (:) and
not an equal (=) symbol. Think of this as meaning "equal by definition." So the
value of V is defined to be equal to the expression above and the value of r is
defined to be equal to 10. This shows that names may be assigned different
kinds of objects.
So, what is V now that r has a numerical value (r is 10) and not itself (r is r)?
(%i4)
V;
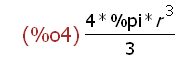
The name V was assigned an expression. It hasn't changed merely because a
value for the name for the radius r was assigned a different value later.
4. Please evaluate V , Maxima, this time with the value of r=10.
(%i5)
''V;
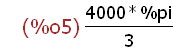
The two single quotes prefixed to the name V ('') causes Maxima to "evaluate" V.
This means that the value of r=10 for the radius is used instead of merely the
value of V which is an expression. The resulting value of the expression is
simplified with r=10 as 4 x 10 x 10 x 10 = 4000. The symbol for the number pi
remains as %pi because this is its value. The name %pi as a symbol for the
number pi is treated differently than a name like r=10. This is why r evaluates
to 10, but pi remains symbolized by %pi. This is generally the behavior of all
irrational numbers that have special symbols in Maxima -- e.g., %e for e, the
natural logarithm base. However, say we want a numerical answer and not an
"exact" symbolic one. A numerical approximation for pi will be have to be used
to do this.
[Note: If r had been assigned the value 10 before V was assigned the above
expression involving the name r, then the value of r would have been 10 at the
time the expression assigned to V was parsed -- means as the characters for the
expression for V were read and interpreted as input. Hence the value for V would
have been simplified as shown in %o6 above. In other words, if Maxima "knows"
the value of r when V was assigned the expression using r, it will do all the
evaluation it can to the expression before it is assigned to V. Since in the above
example the value of r was itself by default at the time the expression was
assigned to V, then that is what was assigned to V. The fact that r was later
assigned the numerical value 10 does not retroactively affect the value of V. This
is why evaluation is required in this case -- to force the expression assigned to V
to use any existing values of names in the expression that is V.]
5. By evaluating V and asking for a numerical form of V the result is a decimal
numeral. What is the is the numerical result of V if r=10?
(%i6)
''V, numer;
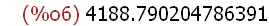
The expression ''V, numer; should be read as: "evaluate the expression assigned
to the name V and return a numerical result."
This Maxima input evaluates the expression named by V by forcing names of
the expression assigned to V which have numerical values to be replaced by
their values. By adding "numer" as a postfix, the numerical approximation for
pi as the double-precision floating-point value 3.141592653589793 is used instead
of the symbol %pi for pi.
3 Expressions
Everything in Maxima is an expression, including mathematical expressions,
objects, and programming constructs. A Maxima expression consists of what
are called "atoms" and operators with arguments.
[Note: It is essential to understand the following: That everything in Maxima is an
expression of one type or another, and that expressions are what Maxima
manipulates. Even statements that are not usually thought of as "expressions"
are expressions as Maxima defines this word. For example, relations such as
a=b or x
different than the expression itself -- e.g., the value of the expression a=b may be
true or false. Think of Maxima expressions as statement objects of different
kinds that have values as attributes. Almost any statement that is meaningful
as Maxima input is an expression that has a value.]
All Maxima expressions are of one of three types -- or classes:
1. Mathematical expressions.
2. Object expressions.
3. Programming construct expressions.
What are instances of these classes of Maxima expressions made of? The
ingredients are of two kinds:
- Atoms.
- Operators with the arguments of that operator.
These classes of expressions and their ingredients (atoms and operators)
are explained below.
[Note: As noted above, all Maxima expressions have a value. This value is what
is displayed by Maxima unless prevented in some way. The value of an expression
may be the expression itself or it may be some other value. When a Maxima
expression is "evaluated" the result is its value. It is important to keep this in
mind: an expression and its value may or may not be the same thing.]
3.1 Mathematical Expressions
These may be composed of "atoms" and "operators" with arguments. For
example in the expression 1+2, the + is an operator (the binary operator
of addition) and it is composed like this as input. The two arguments to
this operator are literal numerals in the form of the two "atoms" 1 and 2.
The expression sin(x) is an operator with one argument, which is the single
letter symbol x -- an atom in the form of a literal name. The value for x may
be itself if no other value has been assigned -- x is x, or x is 10 (from x:10)
for example.
An atom is a name (a single character symbol like V, x and r above, or a name
with more than one character ), a string enclosed in quotation marks (e.g.,
"volume" and "radius"), or a numeral -- i.e., literal integers or decimal
numerals such as 1, -5, 3.14159, etc.
[Note: More on what is meant by "atoms" in Maxima:
1. Names (literal symbols for things) -- x, y, z1, V, r, answer, %pi, energy, mass, c,
delta, eps, and so forth. These names always have a value (the name itself) or
an assigned value. A name is the only type of atom that may have a value other
than itself.
2. Strings (one or more characters enclosed in double quote characters) -- ("a
string") and not two adjacent single quote characters (' ' not a string ' ') The
value of a string as an expression is always itself.
3. Literal numerals (place value numerals, usually base 10; either as integers or
floating point in some form) -- 1, -255, 3.14159, 2.718281828459045d0,
1.0b0, 12.16478e-2, are some examples of permitted forms of literal
numerals that Maxima considers to be atoms. The value of a numeral as an
expression or part of an expression is always itself.]
What is not atomic in Maxima is called non-atomic. All non-atomic expressions
are represented as op(a1, . . . , an) where op is the name of an operator and
(a1, . . . , an) are its n arguments. The expressions may be input and displayed
in a different way, but the internal representation is always in the form of
op(a1, . . . , an). The arguments of an operation can be atoms or non-atomic
expressions. [Note: literally "non-atoms"]
[Note: All expressions that are not simply atoms are "non-atomic" and are
operators -- always internally (to Maxima) of the form op(a1, . . . , an). This
includes basic arithmetic operations such as addition, subtraction,
multiplication, and division which are input conventionally using the symbols + * - /.
However, Maxima "sees" this in the form op(a,b) -- for example 1+2 is seen in the
form of op(1,2) where "op" is the appropriate operation for addition. While it may
not be technically correct, think of a+b as operation sum(a,b). The expression (1+2)
is non-atomic (an operation) but it has two atomic arguments -- the integers 1 and 2.
Its value is atomic however -- (1 + 2)=3. The purpose of using parentheses here is
to emphasize this concept -- an expression conceptually of the form (a op b) is a
non-atomic expression and is a single entity internally -- op(a,b) with two arguments
a and b. The value of this expression is atomic -- the numeral 3.]
Mathematical expressions have mathematical operators (such as + - * / < = >) or
a function evaluations such as sin(x), bessel j(n, x). In such cases, the operator is
the function name.
[Note: There is more being said here than it seems. Maxima expressions (as well
as equivalent mathematical expressions) may be simple or complex --
depending on the ingredients, that is, the mixture of atoms and operators.
Mathematical expressions may be as simple as a single name or numeral -- the
fact that the word "number" is intentionally being avoided here should not be
interpreted as mere pedantry. Simple expressions might be considered to be
the symbol x as a name or 1.618034 or 3!. Complex mathematical expressions
may involve combinations of names, literal numerals, and operators. Literal
numerals include constants with special Maxima names such as %pi and %e.
Since the usual sets of numbers are without an upper or lower bound,
theoretically, these form a class of possible expressions that is unbounded --
while the possible combinations of operators and atoms may be both
theoretically and practically bounded, there are no such theoretical bounds for
numbers. However, due to physical and temporal realities, there are
technical and practical limitations to numerals -- floating point and integer. In any
case we are dealing with a really BIG number (whatever that means)
of possible practical expressions.This class of all possible expressions may be
partitioned in a sense into equivalent classes -- that is the class of all possible
expressions may be partitioned into mutually exclusive equivalence classes where
the attribute defining each subset is the value of the expression.
In addition to a value, each (non-atomic) Maxima expression will have an overall
op attribute that also characterizes the expression in a sense -- see the related
discussion below.
The point that should be emphasized is that while we talk about numbers, we
manipulate symbols -- "numerals" in the form of expressions. Even simple
place value literal whole numbers are in the end, in general, simply expressions
in the form of sums of products of digits between 0-9 and powers of 10.
Maxima provides insight into the essential role expressions have in mathematics.
When you think about it, most of the important action in mathematics
involves expressions and relations between expressions as symbols. Why do we
say that 1/4 = 3/12 is true? Because these expressions belong to the same
equivalence class defined by an attribute which is the rational number they both
symbolize -- their "value." There is something about the rational number
"one-fourth" that is captured by both numerical expressions. The expression in
lowest terms (1/4) has no more or less "one-fourthiness" than any other expresssion
(such as 3/12) that has the number "one-fourth" as its value. ]
3.2 Object Expressions
In Maxima objects are also expressions.
Examples:
A list [a1, . . . , an] of n objects is an object expression.
A matrix object is an expression --
matrix(list((a1,1), (a1,2),. . . , (a1,n)), . . . , list((am,1), (am,2),. . . , (am,n)))
[Note: So a list is an object expression created with the list operation (op = list)
and arguments. A matrix is another object expression created with
the matrix operation (op = matrix) with list object expressions as arguments. Thus
arguments may be atomic or non-atomic. In the case of the matrix above,
the arguments are non-atomic -- they are list object expressions each of which which
may or may not have atomic arguments. The value of these expressions is the
list object or the matrix object which results. So again it is clear that there are
expressions and values of those expressions.
Note that while all expressions have a value, in general the value of an expression
may be lost unless the expression is assigned a name using the the : operator.
Merely entering an expression as Maxima input will result in the display of the
value of the expression (unless suppressed), and then the object and its value passes
out out existence. Sometimes this is okay, for example when Maxima is being used
like a symbolic calculator. However, Maxima has a built-in feature that mitigates this
issue significantly.
The special Maxima name % is assigned the value of the last entered expression and
may be used like any name assigned a value. Of course, the value of % changes with
each new expression entered as input. The values of each entered expression are saved
in the special names prefixed as %o with a sequential numeral for each line of output
These %o names (e.g, %o1, %o2, ..., %on) may be used in Maxima expressions as
names with the values of the displayed output.
The downside to the frequent use of this feature is that these generic names generated
by Maxima have little if any literal significance. One can easily recognize that V means
volume and r means radius, but what does %*(%o7-%o5)/%o3 signify?
The examples below briefly illustrate how this feature may be used:]
(%i7)
%o6;
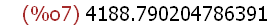
In the example above the Maxima special name %o7 was automatically assigned
the numeral shown (an atom) as a value. What is the value of the % name now?
(%i8)
%;
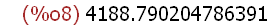
The value of the special name % is assigned the value of %o7, the value of the
last expression input -- the name %o7. Thus the value of the special name %
changes every time an expression is input to Maxima. The value of %o7 and
all other similar special names do not change.
This feature can be quite handy in that it often alleviates the need to
continually assign values to names. However, using these special names may
also result in some unintended side effects if care is not exercised.
3.3 Programming Constructs
These are also expressions. A code block as in block(a1, . . . , an) is an
expression with operator (op = block) and arguments (a1, . . . , an). A conditional
statement (if a then b elseif c then d) is an expression if (a, b, c, d). A loop
(for a in L do S) is an expression similar to mdoin(a, L, S).
[Note: This explains the third class of Maxima expressions -- programming
construct expressions. Code blocks (defined using op = block), conditional
statements (defined using op = if) and loops (defined using op = mdoin) are all
examples of programming construct expressions. Of course these are not
entered as expressions using the these op(a1, . . . , an) forms, but internally
this is how Maxima interprets these expressions.
Now it turns out that Maxima provides two functions to help evaluate what kind
of expression you are dealing with. First, the atom(expr) function, which has
an expression as an argument, will tell you if Maxima "sees" the expression as
being simply atomic. Second, the op(expr) function will return what Maxima
"sees" as the overall operation of an expression argument if it is not atomic.
Expressions of this class have values also which vary according to the type
of programming construct. For example, the value of a loop expression may
be "done" while the value of a block expression is the value of the last
agrument listed.]
The Maxima function op(expr) returns the operator of a non-atomic expression.
The function args(expr) returns the arguments of a non-atomic expression.
The function atom(expr) tells whether an expression is an atom. Using these
functions reveals useful information about how Maxima "sees" expressions.
3.4 Examples of Maxima Expressions
1. Atoms are symbols, strings, and numbers. Several examples below are
grouped into a list object expression so they can be seen together:
(%i9)
[a, foo, foo_bar, "Hello, world!", 42, 17.29];
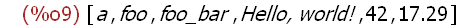
[Note: These are all either names (literal symbols), a string, an integer or a
floating point number -- here as a simple integer (42) and a decimal
number (17.29). No values have been assigned; the value of each of these
atoms is itself .]
2. Mathematical expressions.
(%i10)
[a + b + c, a * b * c, foo = bar, a*b < c*d];
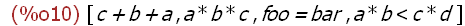
[Note: You can see from this list object expression that mathematical
expressions may simply be combinations of atoms and operators or may also
be relations between expressions. For example foo=bar is considered to be a
mathematical expression. However, keep in mind that this expression
does not say that foo IS EQUAL TO bar, instead it is merely an expression of a
relation between (in this case two atoms) the names foo and bar. The relation
may not hold between foo and bar depending on their values. If the value of foo
is the same as the value of bar then the relation holds. If not, then it does
not, it is as simple as that. Assign nothing to the name foo and assign the name
foo to the name bar and this expression has the value of true. The same is true
for the relation between the product of a and b and c and d. In this case the
relation is not an an expression involving merely atoms -- the names. This may
seem odd to consider a relation to be a mathematical expression. However,
when you think about it there is some good sense in this. If you input op(a*b
and the arguments to the operation are the two product operations on the atoms--
a,b,c,and d. The value of this expression (true or false) will depend on the values
of these name atoms.]
3. Object Expressions -- Lists and matrices.
The elements of a list or matrix can be any kind of expression, even other list
or matrix objects.
(%i11)
L:[a, b, c, %pi, %e, 1729, 1/(a*d - b*c)];
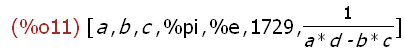
This input is a list object expression assigned to the name L. The elements of this
list are all atoms except the last which is a mathematical expression.
(%i12)
L2:[a, b, [c, %pi, [%e, 1729], 1/(a*d - b*c)]];
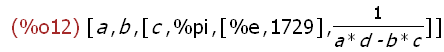
This input is a different list object expression assigned to the name L2. The last
element is itself a list object consisting of two atoms, another list object and a
mathematical expression. These objects result in index names being created
when assigned to a name. These values are accessed by appending brackets
to the object name:
(%i13)
L[7];
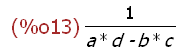
This instance of the list object named L is a mathematical expression.
(%i14)
L2[3];
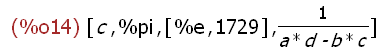
This instance of the list object named L2 is itself a list.
(%i15)
M:matrix ([%pi, 17], [29, %e]);
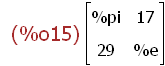
This input assigns an matrix object expression to the name M with atoms as
elements of the of the list object as arguments of the object expression.
(%i16)
M2:matrix ([[%pi, 17], a*d - b*c], [matrix ([1, a], [b, 7]), %e]);
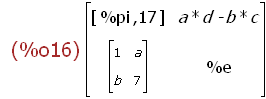
This input assigns a different matrix object expression to the name M2 with
atoms, a list and a matrix object as elements of the of the list object as
arguments of the matrix object expression.
(%i17)
M[2][1];
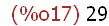
The element of the second row and first column of matrix object M -- the atom 29.
(%i18)
M2[2][1];
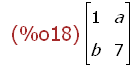
This is the name of the element of the second row and first column of matrix object M2
-- the matrix object as shown.
[Note: The above are all instances of list object expressions or matrix object
expressions. The main point to notice here are that lists and matrix objects
may be created with different types of expressions as arguments -- mathematical
expressions, simple atoms, object expressions, etc.]
4. Programming constructs
These are expressions such as x : y which means assign y to x; the value of the
assignment expression is the value of y.
[Note: There is probably no better example of the difference between an
expression and its value than this object. This expression is always non-atomic,
but its value is atomic if the value of y is atomic.]
The block operation groups several expressions, and evaluates them one after
another; the value of the block operation expression is the value of the last
expression of the block. Try to guess the value of the expression below before
entering it as input.
(%i19)
("a block", a:42) - ("another block", b:17);

[Note: This expression is the difference between the values of two block
expressions. The string atoms that are the first argument of each block
do nothing. They are unassigned atoms and they pass out of existence
after the value of the statement is displayed. Their purpose is to merely
serve as arguments to demonstrate a block expression.
This input does two things in one statement. First, it assigns 42 to the
name a and 17 to the name b, and then it performs the difference operation
using the value of these assigment statements as arguments.
However, an assignment is not itself an operation. If op(a:42) is input, an
error message results. This is because Maxima "sees" a:42 as an atom.
Input atom(a:42) and the value is true. (a:42) - (b:17) is merely a
mathematical expression with two atoms as arguments. The value of this
expression is 25. If you input op((a:42) - (b:17)) the result is +. This apparent
oddity is due to the fact that Maxima is true to mathematics in the sense that
subtraction is defined in terms of the sum of a and the additive inverse of b
-- a - b means by definition a + (-b).]
(%i20)
[a, b];
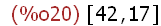
The string atoms of the block expressions were lost, and the block expressions
themselves are gone (except using the % and %o names), but the names a and b
were assigned values that persist. This is a list expression object formed using the
atoms a and b as arguments with values 42 and 17 respectively. Notice that since
Maxima "knows" that values have been assigned to the names a & b. When this
input for the list expression is parsed the list object is created with using the values
of a and b and not the names a and b.]
(%i21)
block ([a], a: 42, a^2 - 1600) + block ([b], b: 5, %pi^b);

This is a Maxima block programming construct object expression that was formed
using two block operations (op=block) with the arguments as shown. Notice that
the block operation returned the value of a^2 - 1600 + block ([b], b: 5, %pi^b).
The last term in this argument was also a block operation. It returned a value
of %pi^5 -- this was added to the 164 from the result of 42^2 -1600 = 164 to
yield the final output of %pi^5 + 164.
(%i22)
(if a > 1 then %pi else %e) + (if b < 0 then 1/2 else 1/7);
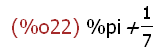
This example shows two programming object expressions as arguments to the
addition operation. The characteristic operation of this expression is addition --
op = +. The arguments are the two if operations that result in the two values
%pi and 1/7 that are the addends of the total expression. Note that the
arguments to the if operations (op is if) may be relational mathematical
expressions -- (a > 1) and (b < 0). These are evaluated as arguments in this
case. What is interesting to note is that because the overall op of this expression
is +, this is a mathematical expression in the end. The values of the op=if
expressions are atomic -- %pi and 1/7. The expressions themselves are
non-atomic.
3.5 Useful Maxima Functions
Certain functions are useful for understanding how Maxima works. The function
op(expr) returns the overall (or characteristic) operator of a expression, args(expr)
returns the arguments, and atom(expr) tells whether an expression is an atom.
Below are some examples:
(%i23)
op(p + q);
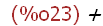
(%i24)
op(p + q > p*q);
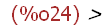
(%i25)
op(sin (p + q));
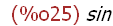
(%i26)
op(foo (p, q));
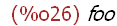
(%i27)
op(foo (p, q) := p - q);
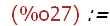
(%i28)
args(p + q);
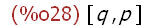
(%i29)
args(p + q > p*q);
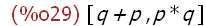
(%i30)
args(sin (p + q));
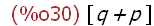
(%i31)
args(foo (p, q));
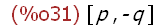
[Note: The list object that returns the arguments of foo(p,q) shows a -q
for the second argument. This is interesting. What happens here is
is displayed from the result of op(foo(p,q)). The value is + even though
the body of the argument is p-q. There is no fooling Maxima. It "knows"
that p-q is defined as p+(-q). Therefore if op=+ is the characteristic
operation of foo(p,q) the arguments must be as in op(p,-q).]
(%i32)
args(foo (p, q) := p - q);
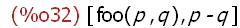
(%i33)
atom(p);
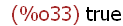
(%i34)
atom(p + q);
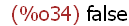
(%i35)
atom(sin (p + q));
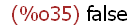
3.6 Expression Construction
The single quote tells Maxima to "construct" the expression but suppresses
"evaluation" of the expression.
[Note: In the examples below the expressions preceded by the single quote
character are not "evaluated" (see the next Section 4) but they are
"constructed." The difference will be clearer after what is meant by
evaluation is explained in the next section. For now, take it on faith that
without the single quote the following examples cause errors due to the fact
that evaluation results in arguments to op() and block() that may not make
sense -- for example, they may be atomic.]
(%i36)
op('(block ([a], a: 42, a^2 - 1600)));
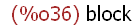
The expression using the block() programming construct [sorry! This is
awkward terminology here ...] is "constructed" as an argument to op(expr), but
it is not evaluated -- it remains a non-atomic expression. Thus the
characteristic operation of this constructed expression is op=block.
[Note: When an expression is evaluated it results in another expression
-- the value. This value may be an atomic or a non-atomic expression. The
single quote prevents the evaluation of the expression it is applied to.
Hence, the expression is constructed, but not evaluated. When an
expression is constructed the result is an expression that is not the value
of the expression. The form of the constructed expression depends on what
the expression is. This means that, for example, unless the expression is
atomic to begin with, the constucted expression will not be atomic, even
though the value of the expression may be atomic. For example,
op('x) results in an error because the value of 'x is x -- it is an atom regardless
of its value and the op() function expects a non-atomic argument.]
(%i37)
x:2+3;
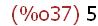
(%i38)
x;
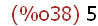
(%i39)
'x;
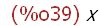
(%i40)
op(x);

(%i41)
op('x);

(%i42)
x;atom(x);

(%i44)
'x;atom('x);

The above examples show that the value of an expression and its constructed
value may be different even if both are atoms.
(%i46)
x:if p > q then p else q;
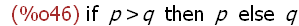
(%i47)
x;'x;
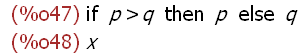
(%i49)
op(x);

(%i50)
op('x);

The above examples show that the value of an expression and its constructed
value may be different when the expression is a non-atomic expression. The value
of x is non-atomic (op=if), but the constructed value is atomic 'x=x.
(%i51)
op('(if p > q then p else q));
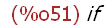
The expression using the if programming construct is constructed as an
argument to op(expr), but it is not evaluated -- it remains a non-atomic
expression. Thus the characteristic operation of this expression is op=if.
Because p and q are atoms with values p=p and q=q, the value of the
expression (if p > q then p else q) is itself.
(%i52)
p:3;q:%pi;(if p > q then p else q);'(if p > q then p else q);
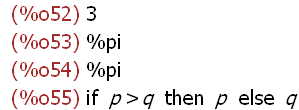
Assign values to the names p and q and then the if expression has a value that
is different from itself (pi). The constructed value is if p > q then p else q -- nothing
is evaluated, but the expression that would be evaluated (the constructed expression)
is the result of using '(if p > q then p else q).
This is also true say, for example, if the expression involves a "for" expression:
(%i56)
op('(for x in L do print (x)));
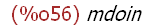
(%i57)
for x in L do print (x);

The value of this expression is "done" as shown above. The characteristic operation of
this expression is op=mdoin. Remember L is the name assigned to a list object expression
above. This expression assigns to the name x each value of the list object L and prints its
value. What would result from the expression: for x in L do print ('x))?
(%i58)
for x in L do print ('x);

The value of the expression has not changed -- it is "done" as it was before. However,
the result is different. For each object of the list L, the above expression prints the
constructed value of x. Since x is atomic, this value is itself and there is one x for
each object of the list.
(%i59)
'(for x in L do print (x));
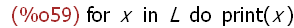
The expression using the "for" programming construct is constructed, but it is
not evaluated -- its constructed value is itself.
(%i60)
args('(block ([a], a: 42, a^2 - 1600)));
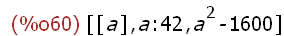
(%i61)
'(block ([a], a: 42, a^2 - 1600));
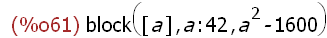
(%i62)
(block ([a], a: 42, a^2 - 1600));
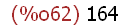
The expression using the block programming construct is constructed as an
argument to args(expr), but it is not evaluated -- it remains a non-atomic
expression. Thus the arguments of this expression are the elements of the list
returned as output from args(expr). The constructed expression has a value
of itself. The value of the expression is 164.
(%i63)
args('(if p > q then p else q));
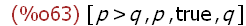
The expression using the if programming construct is constructed as an
argument to args(expr), but it is not evaluated -- it remains a non-atomic
expression. Thus the arguments of this expression are the elements of the list
returned as output from args(expr).
(%i64)
args('(for x in L do print (x)));

The expression using the for programming construct is constructed as an
argument to args(expr), but it is not evaluated -- it remains a non-atomic
expression. Thus the arguments of this expression are the elements of the list
returned as output from args(expr). These are arguments to the op=mdoin
operation which was prevented from being evaluated. The evaluation of this
expression results in the instances of the name L being displayed. L should
be a list or set object for example or an error results. This error is avoided
because the expression is "constructed" but not evaluated.
From these examples you can see that constructing an expression means
that Maxima stops short of evaluating the constructed expression. What is
it that is "constructed" in each case above? As always, some kind of an
expression. For example:
mdoin(x,L,false,false,false,false,print(x))
Evaluation of the expression that resulted in this expression results in a display
of a listing of the instances of the object L are -- if L is defined as a set or list
object. If L is not defined, then evaluation results in an error -- Maxima expects
something to iterate through in the form of an object that has some instances
it contains. It complains if this is not satisfied during evaluation.
In summary, the single quote directs that an expression be constructed, but
not evaluated. The result is often a non-atomic expression of some kind --
most commonly an operation. However, in some cases the constructed
expression is atomic.
If the constructed result is assigned a name, say expr, then the expression
input as ''(expr) would display the value of the constructed expression.
This leads the discussion to consider evaluation in more detail in the
next section.
(%i65)
expr:'(for x in L do print (x));
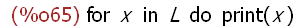
(%i66)
''expr;

This is equivalent to ''('(for x in L do print (x))).
This is essentially the process Maxima uses for evaluation -- the constructed value
of an expression is evaluated. This value depends on the expression.
4 Evaluation
The value of a symbol (name or identifier) is an expression associated with the
symbol. Every symbol has a value. If not otherwise assigned a value, a symbol
evaluates to itself -- e.g., x evaluates to x if not otherwise assigned a value.
[Note: Every name (symbol) used in Maxima is defined when first used and
acquires some value either itself as an identity (x=x) or an assigned expression --
either atomic or non-atomic.]
* Evaluation of Atomic Expressions
------------------------------------------------
Numbers and strings are atoms and always evaluate to themselves. Names are
atoms and evaluate to themselves or to an assigned value -- an expression
which may be atomic or non-atomic.
* Evaluation of Non-atomic Expressions
------------------------------------------------------
Non-atomic expressions are evaluated approximately as follows:
1. Each argument of the operator of the expression is evaluated.
[Note: Remember each operator expression has an overall
characteristic operation and arguments to that operation -- op(expr)
and args(expr).
2. If an operator is associated with a callable function, the function is called,
and the return value of the function is the value of the expression.
[Note: The function definition operator -- f(a1, ... , an) := expr -- defines
a function named f with arguments (a1, ... , an) and function body expr.
Thus f is a callable function. A defined function is an operator expression.
Hence its value is the return value of the function determined by expr. For
example, for the function definition statement -- foo (p, q) := p - q) --
op(foo(p,q)) = foo and the value of foo(p,q) is p-q. If p and q have
assigned values they are evaluated as arguments (step 1, above) and
then the value of p-q is returned as the value of foo(p,q). If either p or q
(or both) have not been assigned a value then the call to foo(p,q) will
return the default value of p or q -- the name itself. In other words,
the behavior for function foo is what you would expect for a function.]
4.1 Modifications of Evaluations
Expressions can be modified in ways that cause less or more evaluation.
* Modifications That Cause Less Evaluation
-----------------------------------------------------------
1. Certain functions do not automatically evaluate some or all of their
arguments, or may otherwise modify the evaluation of their
arguments.
2. A single quote character (') as a prefix prevents evaluation, but not
construction of an expression -- see the section above about expression
construction.
(a) 'x, where x is a name, evaluates to x. Any other value of x is ignored.
(b) 'f(a1, . . . , an) evaluates to f(ev(a1), . . . , ev(an)). That is, the
arguments are evaluated but f is not called.
[Note: The effect of the single quote here is to circumvent step 2
above for the evaluation of non-atomic expressions -- for 'foo(p,q),
foo itself is not called. The notation ev(a1), etc. means, that each of
the args is still evaluated by this form of the call to foo. So what is
returned is what the call to the function would be with the values of
each argument. In other words, this modification returns what the
function call is with the arguments evaluated and not the return
value of the function.]
(c) '(. . .) prevents evaluation of any expressions inside the round
brackets (. . .).
[Note: As is conventional, parentheses are used as a method to
group symbols to be considered as one. Thus any expr enclosed in
parentheses with a single quote prefix is affected in totality -- for
example, for '(foo(p,q)) foo is not evaluated and neither are the
arguments p and q. Thus foo(p,q) is the returned value.]
* Modifications That Cause More Evaluation
------------------------------------------------------------
1. Two single quotes ('') cause an extra evaluation at the time the expression
is parsed as input. This means that modification occurs only at input time
for expressions prefixed with ''. When applied to a general expression
(e.g., ''expr) , causes the value of expr to be substituted for expr in the
input expression.
[Note: This is a one time effect at time of input parsing of an expression.
Recall the first example of the expression named V for the volume
of a sphere. The value for the radius named r was assigned after the
name V was assigned the expression for the volume that included
the name r. Double quoting V was required to evaluate V at the
assigned value of r. Without the double quoting V returns its value
which is the expression it was assigned with r unevaluated.]
2. ev(a) causes an extra evaluation of a every time ev(a) is evaluated.
[Note: The expression ev(expr, a1,a2, ... an) evaluates the
expression expr "in the environment of" the arguments
a1,a2, ... an. These arguments may be flags ("Boolean switches"),
assignments, equations, and functions. The result of evaluating expr
in this argument "environment" is the expression returned by ev().
See the Maxima documentation for the details of how the steps of
this evaluation are accomplished. In the example of the volume of the
sphere the expression ev(V,r=10) evaluates V in the environment
of a radius of value 10. The value of V is not affected. An alternative
way to express this is simply V, r=10 which means the value of V
with a radius of 10. If r had been assigned a value as in r:5 and
the issue is to evaluate V with r=10 then this form serves that
purpose. The the values assigned to V and r are not affected.]
3. The idiom apply(f, [a1, a2, . . . , an]) causes the evaluation of the arguments
(a1, . . . , an) even if f ordinarily "quotes" them.
[Note: As explained above, some functions do not evaluate some or all
of their arguments when called. This is similar to f(a1, 'a2, . . . , an)
for example where the funtion f for whatever reason does not evaluate
the argument a2. Using apply forces evaluation of the arguments
(a1, a2, . . . , an) of function f for such cases. This expression means apply
to the function f each of the instances of the list object [a1, . . . , an] as
arguments to f. The structure of the list as arguments to f must be
compatible with the argument requirements of f -- if f is foo(p,q) then
the list must have two instances that are acceptable arguments to foo,
that is, [a1,a2] in this case.]
4. The define(f (a1, . . . , an), expr) function constructs a function definition
like f(a1, . . . , an) := expr, but evaluates the function body (expr) while :=
does not.
[Note: The := operation does not evaluate the function body (expr)
when used in a function definition statement. The statement
define (foo(a1, ..., an), expr) defines the function foo as expr and
evaluates expr. In the example of the volume of the sphere the
expression p:4/3 and a function definition expression of the form
V(r):=p * %pi * r^3 would not result in the evaluation of expr as a
value for V(r). The value of V(r) is p * %pi * r^3 in spite of the fact
that the value of p is 4/3. the expression define(V(r),p * %pi * r^3)
results in a value for V(r) in the form of an expression that includes
the evaluation of p -- V is (4/3)* %pi * r^3. Don't try this with the
argument r having an assigned value -- an error results because
r is an argument of f and not merely part of the expression used
to define f.]
The following sections explain and provide some examples of evaluation.
4.2 Default Evaluation
Symbols evaluate to themselves if not otherwise assigned a value. If
assigned a value names evaluate to those values.
(%i67)
block(a: 1, b: 2, e: 5);

A block expression assigning values to the names a, b and e. The return value is
the value of the last expression in the block -- e=5 in this case. These are atoms.
(%i68)
[a, b, c, d, e];
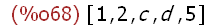
An list object expression with the names a,b,c,d,e as elements. The return value
is a list of values of the elements. In this case atoms a, b and e evaluate to assigned
values, while d and e do not, so the values for these names are the names
themselves. Again, these are all atoms.
4.3 Evaluation of Arguments
Arguments of operators are ordinarily evaluated -- unless evaluation is prevented
in some way.
(%i69)
block(x: %pi, y: %e);

(%i70)
x;y;

A block expression assigning values to the names x and y. The return value is the
value of the last expression in the block -- %e in this case. These are atoms. The
arguments were evaluated. Hence the return value for x of %pi and not x.
(%i72)
sin(x + y);
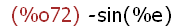
The sin() function evaluates using values assigned to the names x and y. The
return value is the value of the the sin(%pi+%e) -- -sin(%e) in this case.
(%i73)
x > y;
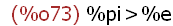
This is a mathematical expression that evaluates using values assigned to the
names x and y. The return value is the expression itself with the the assigned
values of the names x=%pi and y=%e in this case.
[Note: So that this is clear, to find out if pi > e is true the expression is(%pi>%e) is
used. This expression if used as an argument will be evaluated. The value of
this expression is true.]
(%i74)
is(x>y);
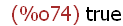
(%i75)
is(x=y);
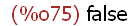
(%i76)
x!;

(%i77)
x!, numer;
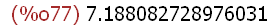
Interesting!
This is a mathematical expression that evaluates using the value assigned to the
name x -- %pi . The return value is the expression itself with the the assigned
values of the names x=%pi in this case.
4.4 Callable Functions
If an operator corresponds to a callable function, the function is called -- unless
prevented. Otherwise evaluation yields another expression with the same
operator.
(%i78)
foo(p, q) := p - q;
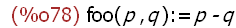
The function foo has been defined using the := operation. It is callable -- meaning
that it will return a value other than itself.
(%i79)
p: %phi;
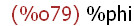
The name p is assigned to the value %phi -- the symbol for the golden mean --
phi.
(%i80)
foo(p, q);
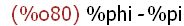
(%i81)
foo(p, q), numer;
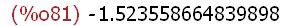
The function foo is called with arguments p and q. Arguments p and q are atoms
(symbols for names) and p has the assigned value %phi (an Maxima literal
constant for the so-called golden mean -- (1 + sqrt(5))/2. The numeric value of
%phi is the double-precision floating-point value 1.618033988749895.
The argument q was not assigned any expression, so its value is itself when
evaluated during the function call. The value of the call to foo is the value of the
evaluated arguments (p and q) applied to the expression used to define foo --
p-q.
(%i82)
bar(p, q);
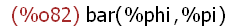
The function bar is not callable with arguments p and q -- it has not been
assigned any expression, merely created as a name. The value of bar is itself.
In spite of this, the arguments (p and q) are evaluated however as displayed.
4.5 Automatically Quoted Arguments
As mentioned previously, some functions "quote" their arguments automatically.
Examples: save(), :=, and kill().
[Note: It is the default behavior of some Maxima functions -- cited here are the
three examples save, kill and := to "quote" their arguments. This means
this automatic behavior is the same as using the single quote character as a
prefix to the argument (e.g., 'a is a, regardless of the value of a.). Thus if foo is
called as foo('p,q) the result is p-q and not %phi-q. This is the way some Maxima
functions behave automatically.]
(%i83)
[foo('p,q),foo(p, 'q),foo('p, 'q)];
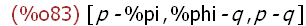
(%i84)
block(a: 1, b: %pi, c: x + y);
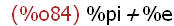
(%i85)
[a, b, c];
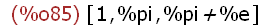
In the last two lines of input the arguments of the expressions were evaluated
automatically.
(%i86)
save("tmp.save", a, b, c);
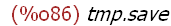
[Note: The save function of the form -- save (filename, name1, name2, name3, ...)
-- stores data in the form of Lisp expressions -- the current values
of name1, name2, name3, ..., in filename. The arguments are the names of
variables, functions, or other objects and the value returned for save is
filename. This function evaluates filename and quotes all other arguments --
here names a, b, and c. The file temp.save has the following as contents:
;;; -*- Mode: LISP; package:maxima; syntax:common-lisp; -*-
(in-package :maxima)
(DSKSETQ $A 1)
(ADD2LNC '$A $VALUES)
(DSKSETQ $B '$%PI)
(ADD2LNC '$B $VALUES)
(DSKSETQ $C '((MPLUS SIMP) $%E $%PI))
(ADD2LNC '$C $VALUES) ]
Notice in this file that there is a single quote prefixed to the arguments and
that the arguments are not evaluated. For a and b this is no huge issue since
these are atoms to begin with so they are the same whether or not evaluated.
However, Notice that c is shown in the file as having a value of
$C '((MPLUS SIMP) $%E $%PI)) which is the constructed argument expression in
the form of an op=+ with arguments (%e,%pi).
This is the same effect as save("tmp.save", 'a, 'b, 'c) only here the quoting of
arguments is automatic.
(%i87)
f(a) := a^b;
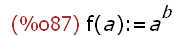
(%i88)
f(7);

Function f is defined using := operation. The argument a and name b are not
evaluated in the value for f(a). However, the call to f(7) results in the
evaluation of argument a and name b. Notice that the value of a was set to 1
above (a:1) but it is evaluated in the function call as an argument to f and
the value in this scope for a is 7. Also notice that the value of b was set to %pi
above (b:%pi) but it is not evaluated. Remember, the := operation does not
evaluate the function body as an argument to a function definition statement
-- and and b are both part of the function body here.
(%i89)
values;
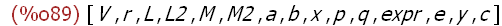
(%i90)
kill(a, b, c, x,expr,L,L2);
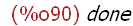
(%i91)
values;
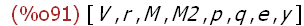
(%i92)
[a, b, c];
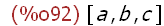
(%i93)
values;
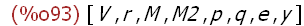
The kill function removes the values from the arguments -- atoms a, b, and c. The
kill function does not evaluate the arguments -- the value of kill is done. The names
a, b, and c were "killed" by this statement and their values were thus lost. The
command values displays a list of all bound user names. The list comprises
symbols assigned expressions using : , ::, or :=. Using the values command after
the kill command shows that the names a, b, and c were no longer listed and their
values were removed. The list expression [a,b,c] references the names a, b, and c
again, but these names have no value assigned and are not saved as bound names.
4.6 Preventing Evaluation
A single quote prevents evaluation even if it would ordinarily happen.
(%i94)
foo(x, y) := y - x;
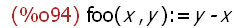
(%i95)
block(a: %e, b: 17);

(%i96)
foo(a, b);
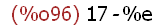
The foo function when called returns the value of the evaluated arguments (a
and b) as expected according to the expression defining the function
-- x - y in this case.
(%i97)
foo('a, 'b);
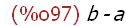
The function foo is called with the arguments single quoted. Thus they are not
evaluated and their names are used as their values instead. This can
be seen from the fact that the result of the call is b - a and not y - x. Which also
means the function foo was evaluated.]
(%i98)
'foo(a, b);

Here the function foo itself is single quoted and hence not evaluated -- but the
arguments (a and b) are. The returned value is the function with the evaluated
arguments.
(%i99)
'(foo(a, b));

The entire function call is now quoted due to the use of the parentheses which is
single quoted enclosing the call to the function. A similar result
can be had using 'foo('a, 'b); as input.
4.7 Extra Evaluation
Two single quotes ('' or quote-quote) causes an extra evaluation at the time
the expression is parsed.
(%i100)
diff(sin (x), x);
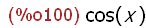
The diff(expr,x) function call returns the derivative (or differential) of expr with
respect to the variable x. The result is cos(x) as expected.
(%i101)
foo(x) := (diff(sin (x), x));
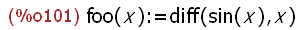
A function foo(x) is defined as the diff(sin(x),x) which returns the derivative (or
differential) of expr with respect to the variable x. The return value repeats the
function definition as parsed. Recall that the := operation does not evaluate the
function body -- i.e., exprx in f(x) :=exprx where exprx is some expression that
defines the function, presumably involving the argument name x . Evakuation
in this case can be accomplished as:
(%i102)
foo(x) := ''(diff(sin (x), x));
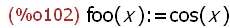
A function foo(x) is now redefined with diff(sin(x),x) prefixed by two single quotes
which returns the evaluated derivative (or differential) of expr with respect to the
variable x.
Here the result of the evaluation of diff(sin(x),x) is cos(x). The return value repeats
the function definition of foo(x) reflecting this evaluation.
Using ev(expr) causes an extra evaluation every time it is itself evaluated.
Contrast this with the effect of quote-quote('') above:
(%i103)
block(xx: yy, yy: zz);
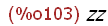
This block expression assigns yy to the name xx and then zz to the name yy.
(%i104)
[xx, yy];
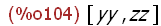
The list expression with names xx and yy as elements returns a list object with the
values of xx and yy as elements -- yy and zz. Now, define a function that uses '' to
force evaluation of the expression that defines the function:
(%i105)
foo(x) := ''x;

The two single quotes prefixed to x caused an extra evaluation of x at the time
that this function definition for foo(x) was parsed, Since x has no value
at the time it was parsed there is no value. The return value repeats the function
definition of foo(x) as is -- foo (x) := x.
(%i106)
foo(x);
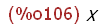
It should be clear that the effect of using '' is one time in this case -- at the point
at which the function was defined since the above shows that the function is
simply the name x as an argument.
(%i107)
foo(xx);
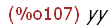
The return value of foo(xx) is the value of xx or yy in this case as expected.
Remember that arguments are evaluated when a function is referenced
("called") with arguments. Now define a similar function using the ev()
operator:
(%i108)
bar(x) := ev (x);
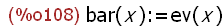
This function definition for bar(x) uses the ev(expr) function instead of two single
quotes. This means that ev(expr) is retained as part of the function
definition for bar(x) as expected. When bar(expr) is called the argument expr will
be evaluated as an argument and then by ev(expr).
(%i109)
bar(xx);
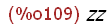
The expression xx is evaluated as xx=yy as the argument to bar(expr). Then
because the function is defined using ev(expr) this is the same as ev(yy) which
returns the value of yy which is zz. This is what is meant by saying that ev(expr) is
evaluated each time it is called.
4.8 Arguments to apply()
Using apply(f,[a1,a2,...,a]) causes the evaluation of arguments to function f of
the list even if they are ordinarily "quoted" by f. In this context "quoted" refers
to how some functions deal with certain arguments as though they are prefixed
by the single quote character '. Recall that arguments are evaluated when a
function is referenced (called) with arguments. Some functions vary from this
behavior by "single quoting" some arguments. For example, if the function
f(x) is called with exprx as an argument as in f(exprx) the usual behavior is
for the argument exprx to be evaluated. Some functions do the equivalent of
the following to one or more arguments: f('expr), thus preventing the
evaluation of exprx.
(%i110)
block(a: aa, b: bb, c: cc);
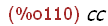
(%i111)
block(aa: 11, bb: 22, cc: 33);
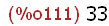
(%i112)
[a, b, c, aa, bb, cc];
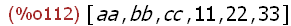
The two block expressions above assign aa to a, bb to b, and cc to c, then 11 to
aa, 22 to bb, and 33 to cc. The list expression above displays these values.
(%i113)
apply(kill, [a, b, c]);
The input kill(a,b,c) would not ordinarily result in the evaluation of arguments a,b,
and c. This would result in kill being applied to a,b, and c. However, if the function
name "kill" is an argument to the apply() function, then the arguments to kill will be
evaluated. In this case the result is the same as kill(aa,bb,cc).
(%i114)
[a, b, c, aa, bb, cc];
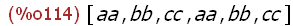
The result of using apply with the kill argument is reflected by the element of the
list object above. The names a,b, and c retain their values -- aa, bb, and cc
respectively. However, the names aa, bb, and cc now have the default values of
themselves respectively since their assigned values were killed.
(%i115)
kill(a, b, c);
When the kill() function is called directly with the arguments a, b, and c, then the
values assigned to these names are killed.
(%i116)
[a, b, c, aa, bb, cc];
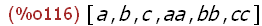
The result of of these two actions is reflected in the elements of the list objects
above. All the names have lost assigned values and assume default values.
In summary, think of the apply function (apply(f,[x]) as "apply to the function f
the evaluated argument x."
4.9 Arguments to define()
Using define(f,[a1,a2,...,an],expr) evaluates the expression (expr) that is body
of the function definition. This is an alternative way to using the form of
f(a1,a2,...,an]):= expr to define a function. Recall that in this case expr is not
evaluated. The define() function defeats this behavior.
(%i117)
integrate(sin (a*x), x, 0, %pi);
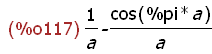
The integrate(expr,x,a,b) results in the symbolic definite integral of expr with
respect to x over the interval a to b. Here this is the integral of sin(ax) from 0 to
pi. This result is shown above. Note that this result does not depend on x. It
depends only on the name a and pi. Since the name a has no assigned value this
result is about as simple as it can get.
(%i118)
ratsimp(integrate (sin(a*x), x, 0, %pi));
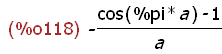
Applying the ratsimp(expr) function results in the "simplest" symbolic form.
Now use this expression to define a function:
(%i119)
foo(x) := integrate(sin(a*x), x, 0, %pi);
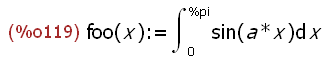
The function foo(x) is defined as the same symbolic definite integral., but the
expression defining foo is not evaluated as the result indicates.
(%i120)
define(foo (x), integrate(sin(a*x), x, 0, %pi));
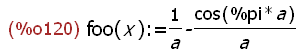
The function foo(x) is defined as the same symbolic definite integral as the
defining expression using the define(foo(x),expr) function. The
expression defining foo is now evaluated as the result indicates.
(%i121)
ratsimp(define(foo(x), integrate(sin (a*x), x, 0, %pi)));
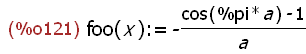
Applying the ratsimp(expr) function results in the same simplest symbolic
form as before. It is interesting to note what results if the name a is
assigned a value.
(%i122)
block(a:3, define(foo (x), integrate(sin(a*x), x, 0, %pi)));

In the above block expression the name a is assigned the value 3. The function
foo(x) =2/3 results when foo is defined.
In summary, think of the define function (define(f,[x],exprx) or define(f(x),exprx))
as "define a function named f with the argument x as the evaluated expression exprx."
5 Simplification
After evaluating an expression, Maxima attempts to find an equivalent expression
which is "simpler." Maxima applies several rules which embody conventional
notions of what is meant by "simplification." For example, 1 + 1 simplifies to 2,
x + x simplifies to 2x, and sin(%pi) simplifies to 0. However, many well-known
identities are not applied automatically. For example, double-angle formulas for
trigonometric functions, or rearrangements of ratios such as a/b + c/b ->
(a + c)/b. There are several functions which can be used to apply identities. for
the purpose of simplification.
Simplification is always applied unless explicitly prevented. Simplification is applied
even if an expression is not evaluated.
Using tellsimpafter establishes user-defined simplification rules.
[Note: Simplification is a matter of convention to some degree. Most people agree
on what "simpler" means in most expression contexts. However, on some points
what is simpler is a matter of personal preference or convention. Why are
fractions expressed in lowest terms simpler? One answer is because someone
said so. Another answer could be because the numerals of the numerator and
denominator are the smallest and so forth. The question of what is meant by
"simpler" is always one that is legitimate. This is why there has to be rules
that determine what "simpler" means. So when "simplification" is used in
the context of Maxima it means simplifcation as defined by Maxima --
or simply Maxima simplfication.]
5.1 Examples of Maxima Simplification
The following are some examples of simplification:
(%i123)
[1 + 1, x + x, x * x, sin(%pi),(a + b)^2,(a/b + c/b),sin(2*x),a * exp(b * %i)];
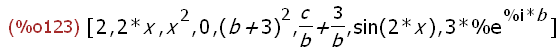
The expressions that are elements of the above list are simplified according
to the Maxima rules of simplification.
A quote single quote character as a prefix prevents evaluation but not
simplification. When the global flag simp is false, simplification is prevented
but not evaluation.
[Note: It is important to make clear the difference between evaluation and
simplification. Recall that evaluation is a process that results in an expression
in terms of the values of the ingredients (atoms and non-atoms) of an expression.
Simplification is an equivalent form of an expression that is "simpler" by some
criteria. One way to think of simplification is in terms of a relation between
equivalent expressions of "simpler than" by way of comparsion. Thus, if A and B
are equivalent expressions (identities) then stating that A "is simpler than" B
implies criteria for "simpler."
(%i124)
'[1 + 1, x + x, x * x, sin(%pi),(a + b)^2,(a/b + c/b),sin(2*x),a * exp (b * %i)];
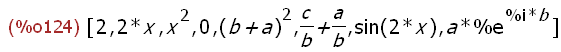
(%i125) simp: false$
The global flag simp is set to the value false. The $ suffix merely prevents the
return value of this input (which is "false") from being displayed as output.
[Note: Assigning the Maxima flag simp to be false (simp:false) will prevent simplification
until it is it is re-assigned a value of true. This can be useful in some cases, but should
be used with caution. Leaving simp set to false can have some unusual side effects
that may not be obvious.]
(%i126)
'[1 + 1, x + x, x * x, sin(%pi),(a + b)^2,(a/b + c/b),sin(2*x),a * exp(b * %i)];
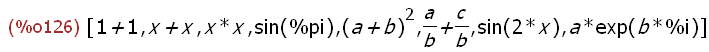
(%i127)
block([x: 1], x + x);
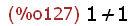
The expressions that are elements of the above list and block expressions are
not simplified due the the simp flag being set to false.
(%i128) kill(all)$simp:true$
Input merely to clear values from names and set simplification flag to true.
5.2 Exceptions to Maxima Simplification
Some identities are not applied automatically. What this means to the user is
that in some cases expected simplifications do not occur. In these cases more
is required in order to simplify certain expressions. Some functions which apply
identities that may result in simpler expressions are expand(), ratsimp(),
trigexpand(), demoivre().
(%i2)
(a + b)^2;
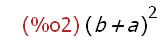
This expression is not automatically expanded into the form of its well-known
equivalent expression.
(%i3)
expand((a + b)^2);
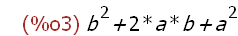
Using expand(expr) does this. You might ask if this latter expression is "simpler"
or not.
(%i4)
a/b + c/b;
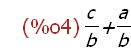
This atonal expression is not automatically simplified into the form of its
well-known equivalent expression with a common denominator.
(%i5)
ratsimp(a/b + c/b);
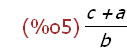
Using ratsimp(expr) does this.
(%i6)
sin(2*x);

This trigonometric expression is not automatically simplified into the form of its
well-known equivalent expression.
(%i7)
trigexpand(sin(2*x));
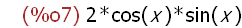
Using trigexpend(expr) does this.
(%i8)
a * exp(b * %i);
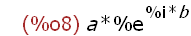
This complex exponential expression is not automatically simplified into the form
of its well-known equivalent trigonometric expression.
(%i9)
demoivre(a * exp (b * %i));
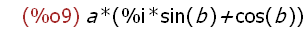
Using demoivre(expr) does this.
6 Special Purpose Functions
6.1 apply()
The function apply(f,[x1, x2, ... , xn]) constructs and evaluates an
expression in the form of f(arg1, arg2, ... , argn) where
arg=x1, arg2=x2, ... , argn=xn. The arguments of the expression
are always evaluated-- even if they wouldn't be otherwise.
(%i10) kill(all)$
Input merely to clear values from names.
(%i1)
apply(sin, [x * %pi]);
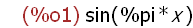
Apply sin to x*%pi.
(%i2)
L1:[a, b, c, x, y, z];
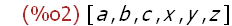
Create a list object atom and make its name L1.
(%i3)
apply("+", L1);
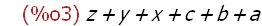
Apply + to elements of list L1.
(%i4)
L2:[1, 5, -10.2, 4, 3];
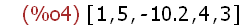
Create a list object atom and make its name L2.
(%i5)
apply(min,L2);
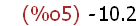
Apply min() function to elements of list L2.
(%i6)
F(x) := x / 1729;
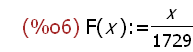
Define a user function F(x).
(%i7)
fname:F;

Assign value F to the name fname.
(%i8)
dispfun(F);
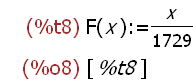
Displays the definition of the user defined function F(x).
(%i9)
dispfun(fname);

The value of fname is F. The name fname is not evaluated as an argument to
since dispfun() quotes its arguments. This is the reason for the error message.
(%i10)
apply(dispfun, [fname]);
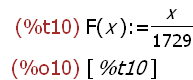
Using apply() forces the evaluation of fname and the function definition is
returned.
6.2 map()
Using the map() function constructs and evaluates an expression for each item in a
list of arguments. The arguments of the expression are always evaluated -- even if
they wouldn't be otherwise. The result is a list object.
(%i11) kill(all)$
(%i1)
map(foo, [x, y, z]);
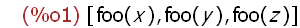
Merely returns foo in terms of each element of the list since foo is not defined,
(%i2)
map("+", [1, 2, 3], [a, b, c]);
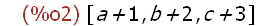
Creates a list of three expressions -- applies + to each element of the two
argument lists. The length of the lists must be the same or an error will result
since "+" is a binary operation.
(%i3)
map("+", [1, 2, 3], [a, b, c], [x, y, z]);
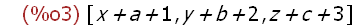
(%i4)
map(atom, [a, b, c, a + b, a + b + c]);

The atom() function is constructed and evaluated for each element of the list.
The first three are atoms the last two are expressions and therefore not atoms.
6.3 lambda()
Using lambda() defines and returns a "lambda" expression (i.e., an "unnamed"
or "anonymous" function). The lambda expression can be used in some contexts
like an ordinary named function. However, lambda does not evaluate the function
body. Think of lambda() as creating
(%i5)
f:lambda ([x, y], (x + y)*(x - y));
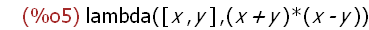
The name f is assigned the lambda expression. No function is defined. No
evaluation takes place.
(%i6)
f(a, b);
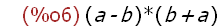
Returns the value of the lambda expression as though it were a function.
However there is no function named f. Instead f has the value of the lambda
expression.
(%i7)
f;
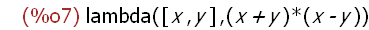
(%i8)
apply(f, [p, q]);
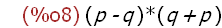
The lambda expression named by f is applied to the elements of the list.
(%i9)
map(f, [1, 2, 3], [a, b, c]);
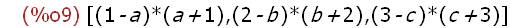
The lambda expression named by f is applied to the elements of the lists
matched in pairs. Returns a list of three expressions one for each pair --
a and 1, b and 2, and c and 3.
In summary, a lambda function is a means to have a name behave as
a function without being defined as a function.
7 Built-in object types
An object is represented as an expression. Like other expressions, an object
comprises an operator and its arguments. The most important built-in object
types are lists, matrices, and sets.
7.1 Lists
1. A literal list is indicated like this: [a, b, c].
2. If L is a list, L[i] is element i of the list. . L[1] is the first element.
3. map(f , L) applies f to each element of L.
4. apply(†+ â€, L) is the sum of the elements of L.
5. for x in L do expr evaluates expr for each element of L.
6. length(L) is the number of elements in L.
Examples:
--------------
(%i10)
L:[a, foo, foo_bar, "Hello, world!", 42, 17.29];
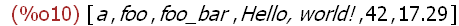
(%i11)
L[1];L[3];
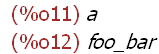
(%i13)
map(display,L)$
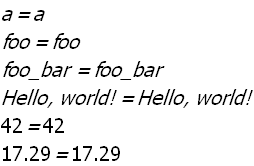
(%i14)
apply("+",L);
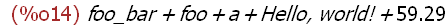
(%i15)
apply("+",[1,2,3,4]);

(%i16)
for e in L do display(e)$
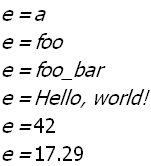
(%i17)
length(L);

7.2 Matrices
1. A matrix is defined like this: matrix(L1 , . . . , Ln ) where L1 , . . . , Ln
are lists which represent the rows of the matrix.
2. If M is a matrix, M [i, j] or M [i][j] is element (i,j). M [1, 1] is
the element at the upper left corner.
3. The operator . represents non-commutative multiplication. M.L, L.M ,
and M.N are non-commutative products, where L is a list and M and
N are matrices.
4. transpose(M ) is the transpose of M.
5. eigenvalues(M ) returns the eigenvalues of M.
6. eigenvectors(M ) returns the eigenvectors of M.
7. length(M ) returns the number of rows of M.
8. length(transpose(M )) returns the number of columns of M.
Examples:
--------------
(%i18)
M:matrix([a, b, [c, %pi, {%e, 1729, 1/(a*d - b*c)}]]);
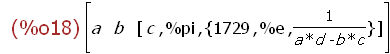
(%i19)
M[1,1];M[1,3];

(%i21)
M[1,3][3];
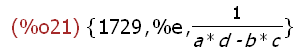
The 3rd element of the matrix M is a list. The above expression has
a value of the 3rd element of that list -- a set object.
(%i22)
M:matrix([1,2],[3,4]);
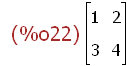
(%i23)
M[1,1];M[2][2];
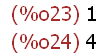
Two different ways to express the elements of a matrix.
(%i25)
transpose(M);
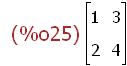
(%i26)
M:matrix([1,2,3,4],[5,6,7,8]);
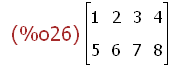
(%i27)
length(M);length(transpose(M));
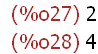
The number of rows and columns of matrix M.
(%i29)
M:matrix([4,1],[3,2]);
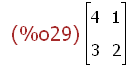
(%i30)
eigenvalues(M);
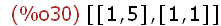
(%i31)
X:eigenvectors(M);
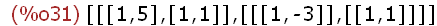
The eigenvalues of matrix M are λ1=1 and λ2=5. The eigenvectors
of matrix M are x1=[1,-3] and x2=[1,1]. Note that eigenvectors()
also returns the eigenvalues as the element of a list.
(%i32)
transpose(X[2]);
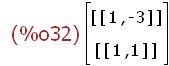
7.3 Sets
1. Maxima understands explicitly-defined finite sets. Sets are not the
same types of objects as are lists. Thus an explicit conversion is
needed to change one into the other.
2. A set is specified like this: {a,b,c, ... } where the set elements are
(a,b,c, ...). An alternative way to specify a set is to use the set
function as in set(a,b,c, ... ).
3. union(A, B) is the union of the sets A and B.
4. intersection(A, B) is the intersection of the sets A and B.
5. cardinality(A) is the number of elements in the set A.
Examples:
--------------
(%i33)
{9,8,7,6,5,4,3,2,1};S:{f,e,d,c,b,a};f;
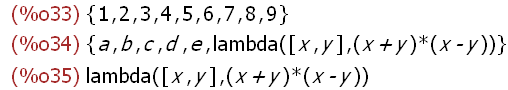
Oops! The name f was assigned a lambda expression previously. Thus
the name f evaluates to this value when S is assigned the set object
expression.
(%i36)
kill(all)$S:set(f,e,d,c,b,a)$f;

(%i3)
S;
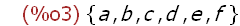
(%i4)
(A:{1,3,5,7,9},B:{1,2,4,6,8,9},union(A,B));
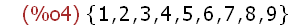
(%i5)
intersection(A,B);
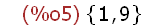
(%i6)
cardinality(union(A,B));cardinality(S);
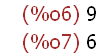
8 Maxima Programming
There is one name space, which contains all Maxima symbols. There is no
way to create another name space. All variables are global unless they
appear in a declaration of local variables. Functions, lambda expressions,
and blocks can have local variables. The value of a variable is whatever
was assigned most recently, either by explicit assignment or by
assignment of a value to a local variable in a block, function, or lambda
expression. This policy is known as dynamic scope. If a variable is a local
variable in a function, lambda expression, or block, its value is local but its
other properties (as established by declare) are global. The function local()
makes a variable local with respect to all properties. By default a function
definition is global, even if it appears inside a function, lambda expression,
or block. local(f ), f (x) := . . . creates a local function definition. trace(foo)
causes Maxima to print an message when the function foo is entered and
exited.
Let's see some examples of Maxima programming.
1. All variables are global unless they appear in a declaration of local
variables. Functions, lambda expressions, and blocks can have local
variables.
(%i8) (x: 42, y: 1729, z: foo*bar)$
(%i9)
f(x, y) := x*y*z;
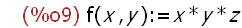
The name z does not appear in as a argument of the function f.
The name z was assigned the mathematical expression foo*bar.
With respect to f the name z is global.
(%i10)
z;
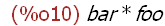
(%i11)
f(aa, bb);
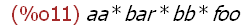
When f is evaluated with x=aa and y=bb, these names are local to f.
The value of the name z is foo*bar and is global in the scope of f.
Maxima rearranges the order of the names that are the factors of
the value of f(aa,bb) alphabetically as shown above. The factors that
are the value of the global name z (foo and bar) appear in that order
together with the values for the arguments of f -- x and y -- which
are aa abd bb respectively. The global names x and y with values
42 and 1729 respectively are not relevant to f.
(%i12)
lambda([x, z], (x - z)/y);
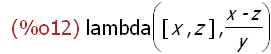
(%i13)
apply(%, [uu, vv]);
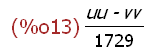
The anonymous lambda expression show above is entered as input.
This expression is assigned as a feature of Maxima as a value to the
name %. This name is used to reference the lambda expression in
the next expression as an argument to the apply() function. Here
the names uu and vv are applied to the lambda function. The result
is the value of the apply function which is shown above. The name
y was not referenced as part of an argument to the lambda
expression. Therefore it is global with respect to the value of the
name %. The names x and z were referenced as part of the
arguments to the lambda expression and so these names are
local with respect to the value of the name %. The global value
of y is evaluated in the above expression as 1729. The global
values of x and z (42 and foo*bar) are irrelevant to the above
expression.
(%i14)
block([y, z], y: 65536, [x, y, z]);
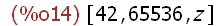
Because the name z was referenced in the first argument of the block
operation that is a list, it becomes local to the block. The last argument
which is returned is the value of the list -- [x,y,z]. The name x is global
and has a value of 42. The name y is local to the block having been
assigned a value of 65536. The name z is local to the block for the
reason above but was assigned no value in the block. Hence the
value of z is itself and that is what is returned.
2. The value of a variable is whatever was assigned most recently, either
by explicit assignment or by assignment of a value to a local variable.
(%i15)
foo(y) := x - y;
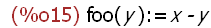
(%i16)
x:1729;
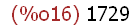
When foo(y) was assigned the expression x-y above the value of x was
itself. Here x is now explicitly assigned the atom 1729.
(%i17)
foo(%pi);

Now when foo is referenced with y=%pi as an argument the result is the
expression above in which the value of x is the explicitly assigned atom
1729. Recall that callable functions are evaluated when referenced.
(%i18)
bar(x) := foo (%e);
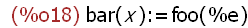
(%i19)
bar(42);
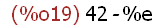
Now the function bar(x) is defined using the value of the expression foo(%e)
which is x-%e. Recall that the expression of a function defined with := is not
evaluated by default. This explains why bar is x-%e and not 42-%e. The
name x is assigned the value 42 as a name local to bar when it is referenced
as bar(42). This is the most recent assignment of a value to x. Therefore when
f(%e) is evaluated in the context of bar the value of x is 42 and not 1729.
9 Some Useful Flags
Maxima provides several system variables that may used in addition to the
simp flag.
When exptdispflag is true, Maxima displays expressions with negative
exponents using quotients, e.g., X^(-1) as 1/X.
(%i20)
kill(all)$
exptdispflag:true;
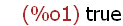
(%i2)
simp:false$
x^-1;
a*x^-2*y*z^-1;
simp:true$
x^-1;
a*x^-2*y*z^-1;
exptdispflag:false$
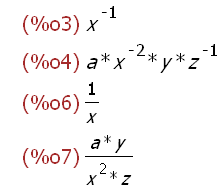
(%i9)
1/x;
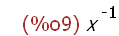
display (arg_1, arg_2, ...)
Displays equations for which left side is each one of the arguments
unevaluated, and whose right side is the value of the expression
centered on the line. This function is useful in blocks and for statements
in order to have intermediate results displayed.
(%i10)
display(sqrt((x*y^2*((x*y^3))^(1/4))^(1/3)));
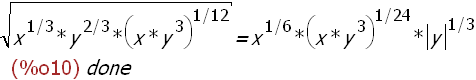
The above output displays the equation with the left hand side (lhs)
being the unevaluated expression that is the argument and with the
right hand side (rhs) being the evaluated expression with whatever
simplification was applied -- depending on the expression. Note two
things -- the displayed ouput is an expression itself (an equality
relation expression) and that this expression is lost after it is displayed
since the value of the display function is "done" and not this equation
expression. To see this use the rhs() function on the output % variable
which should return the right-hand side of a relation expression like
this one:
(%i11)
rhs(%);

The result is 0. This makes sense since the rhs of the expression "done"
is 0.
There is another way to get at manipulating this kind of output -- the
ldisplay() function:
ldisplay (arg1, arg2, ... , argn)
Displays expressions arg1, arg2, ... , argn to the console as printed output.
Each expression is printed as an equation of the form lhs = rhs in which lhs
is one of the arguments of ldisplay and rhs is its value. The ldisplay() function
assigns an intermediate expression label to each equation and returns the
list of labels. The labels hold the value the the equation expressions.
(%i12)
ldisplay(sqrt((x*y^2*((x*y^3))^(1/4))^(1/3)));
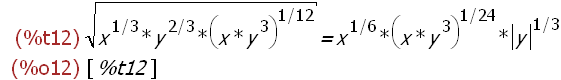
(%i13)
%t12;
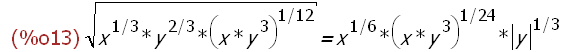
(%i14)
rhs(%t12);
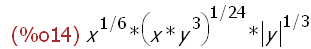
The expression that results from the ldisplay() function is not
"done" rather it is a labeled name -- %t11 in this case. This
name holds the value of the equation expression that was the
result of the ldisplay() function. This label works like any other
name -- it has an expression as a value. The rhs() function
results in an expression that is the right hand side of the
equation relation.
There are many useful Maxima flags (option variables) that may
be used to alter the behavior of Maxima and functions for getting
desired results. Refer to the Maxima Manual for a complete
description of these flags and functions. This how-to has
demonstrated the use of a few of these. The last one now follows:
%edispflag
When %edispflag is true, Maxima displays %e to a negative exponent
as a quotient.
(%i15)
%e^-2;
%edispflag:true$
%e^-2;
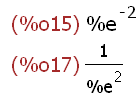
10 Summary
The above sections cover most of the material of the Minimal Maxima document. The
section of this document for specific how-to examples has been intentionally omitted
as these are included in separate how-to subjects.
The above examples and explanation does not exhaust all the features
applicable to Maxima basics. There is enough demonstrated here that is useful
to for most common purposes. The reader is directed to the Maxima documentation
related to set objects and related topics for more information and examples.