Modulo-Rechnen, Zahlentheorie

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

Hilfen zum Handling
Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.
Dazu Shift halten, dann werden auch alle Unterebenen aufgeklappt.
Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.
Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf,
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

Figure 1: Inhaltsverzeichnis

1 Zahlen, Teilbakkeit, Vielfache

1.1 Ganze Zahlen, Ganzzahlige Division

In der Zahlentheorie kommen nur die Ganzen Zahlen vor.
Dezimalzahlen spielen keine Rolle.
Bei Divisionen interessiert man sich für den ganzzahlichen Anteil und den Rest.

(%i1) 34/7;
divide(34,7);

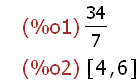
also 34 geteilt durch 7 ist 4 Ganze Rest 7 (wie in der Grundschule)

(%i3) num(34/7);
denom(34/7);

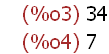
Zähler (numerator) und Nenner (denominator) kann man aus
Brüchen herausgreifen.

1.2 Primfaktoren und Teiler

(%i5) factor(731);
divisors(731);

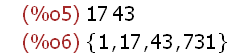
(%i7) factor(72);
ifactors(72);
divisors(72);

(%i10) factor(123456789);

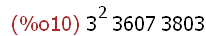
Die Zerlegung in Faktoren zeigt die Primfaktoren und ihre Potenzen.
Bei ifactors werden diese als Liste von Primahlen mit ihren Potenzen
ausgegeben. (integer =ganzzahlig)
Die Teiler einer Zahl sind alle Produkte, sich mit diesen Bausteinen
bilden lassen. Z.B. ist 3*3607 Teiler, aber auch 3^2*3803

(%i11) 3*3607; 3^2*3803;

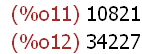
(%i13) divide(123456789,10821); divide(123456789,34227);

Der Rest 0 war also vorherzusehen.

der Befehl divisors(n) zeigt die Teilemenge von n.

(%i15) divisors(3607);

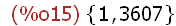
Die Zahlen, die nur sich und die 1 als Teiler haben, heißen Primzahlen.
3607 ist also eine Primzahl.
Achtung: 1 ist keine Primzahl, das ist so definiert.

1.3 Gemeinsame Teiler, ggT

(%i16) divisors(72); divisors(48);

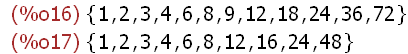
Der größte gemeinsame Teiler ist ersichtlich 24.
Dafür gibt es den Begriff ggT(72,48) in Deutsch und in Eglisch
gcd(72,48) greatest common divisor

(%i18) gcd(72,48);

(%i19) divisors(24);

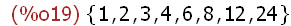
In dieser Teilermenge sind tatsächlich alle gemeinsamen Elemente von
den obigen beiden Teilermengen und 24 ist die größte unter ihnen.

Es gibt den Euklidischen Algorithmus auch in seiner erweiterten Form

(%i20) gcdex(72,48);

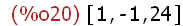
gcdex(a,b) ist so zu lesen: [r,s,gcd] mit r*a+s*b=gcd(a,b)
Also hier

(%i21) 1*72+(-1)*48=24;

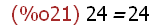
Diese "Vielfachsummendarstellung" wird in der Kryptografie sehr wichtig.
An passender Stelle wird dies aufgegriffen.
Achtung andere Software schreibt [gcd,r,s].

1.4 Vielfache und Gemeinsame Vielfache

Die Vielfachenmengen sind naturgemäß unendlich groß.
Hier nehmen wir 10 Elemente. Wir bleiben im Positiven, damit es übersichtlich bleibt.)

(%i22) Z:makelist(i,i,0,10);

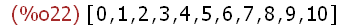
Erstmal erzeugen wir und die Grundmenge Z (eigentlich noch mit Negativen)

(%i23) 6*Z;

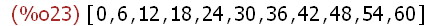
Das ist die abgekürzte Vielfachenmenge 6 Z als Liste.

(%i24) 8*Z;

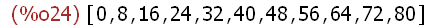
Unter den gemeinsamen Elementen von 6Z und 8Z ist 24 das kleinste
kgV(6,8)=24 in Deutsch, in Englisch lcm(6,8) least common multiple

(%i25) lcm(6,8);

2 Die Gruppe Z(m) und das Modulo-Rechnen

2.1 modulo - Begriff, Z(m)

Es kommt hier nur auf die Reste an, die beim ganzzahligen Teilen bleiben.
In mathematischer Schreibweise 34 mod 7 = 6 (lies 34 modulo 7 ist 6)

(%i26) mod(34,7);

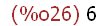
Nehmen wir von allen ganzen Zahlen immer nur den Rest modulo 7
so erhalten wir offfenbar eine sehr kleine Menge, sie heißt Z(7)

(%i27) Z;

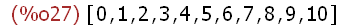
(%i28) mod(Z,7);
unique(mod(Z,7));

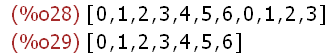
Jetzt nehmen wir negative Zahlen hinzu

(%i30) ZZ: makelist(i,i,-10,20);

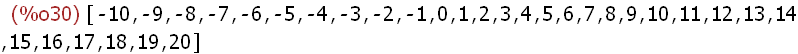
(%i31) mod(ZZ,7);
unique(mod(ZZ,7));

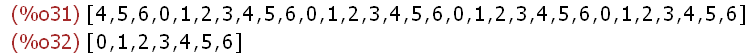
unique wirft die Doppelungen weg. Wir definieren also:

(%i33) Z(m__):=unique(mod(ZZ,m__))$

(%i34) Z(3); Z(7); Z(16);

2.2 Rechnen in Z(m)

Mit den Zahlen dieser Menge kann man nun die Grundrechenarten
+,-, *, hoch unbeschränkt ausführen, "geteilt" gehört nicht dazu.
Grundprinzip ist, dass man wie in ganzen Zahlen rechnet und alles modulo m
interpretiert.

(%i37) 11+13;
mod(11+13,16);

(%i39) 11-13;
mod(11-13,16);

Wenn man das selbst rechnen will, zählt man zu der -2 eine 16 hinzu, ist 14.
Oder man denkt 11=27 mod 16 und 27-13 =14

(%i41) mod(11,16); mod(27,16);

Man kann an jeder Stelle des Rechenvorgangs modulo m "herunternbrechen.
Das ist besonders interessant beim Potenzieren

(%i43) mod(3^5,10);

selber: 3^2 =-1 mod 10 , 3^4=(3^2)^2=(-1)^2 mod 10 =1 mod 10;
3^5=1*3 mod 10=3

(%i44) 3^5;

Da sieht man die 3 auch gleich als Rest beim Teilen durch 10.

2.3 Multplikationstafeln von Z(m)

(%i45) /*Definitionen, nach Auwertung wieder zuklappen */
plus(i,j,m):=mod(Z(m)[i]+Z(m)[j],m)$
maal(i,j,m):=mod(Z(m)[i]*Z(m)[j],m)$
plustafel(m):=block(
    array(ma,fixnum,m,m),
    for i:1 thru m do for j:1 thru m do ma[i,j]:plus(i,j,m),
    print("Plus-Tafel modulo ",m),
    genmatrix(ma,m,m)
)$
maltafel(m):=block(
    array(ma,fixnum,m-1,m-1),
    for i:1 thru m-1 do for j:1 thru m-1 do ma[i,j]:maal(i+1,j+1,m),
    print("Mal-Tafel modulo ",m),
    genmatrix(ma,m-1,m-1)
)$

(%i49) m:6;Z(m);Z(m)[3];

(%i52) plustafel(6);

(%i53) maltafel(6);

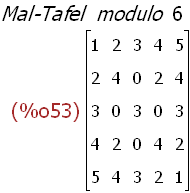
(%i54) for i:4 thru 11 do print(maltafel(i))$

2.4 Zstern(m) die Gruppe der Teilerfremden

Teilerfremd zu m sind alle Zahlen i mit ggT(m,i)=1

(%i55) /*Definitionen Zstern(m) und malsterntafel(m)*/
Zstern(m):=block([li],
    li:[],
    for i:1 thru m-1 do
        if gcd(m,i)=1 then li:endcons(i,li),
    return(li)
)$
malsterntafel(m):=block([le,Zs,malstern],
    Zs:Zstern(m), le:length(Zs),
    malstern(i,j,m):=(mod(Zs[i]*Zs[j],m)),
    array(ma,fixnum,le,le),
    for i:1 thru le do for j:1 thru le do ma[i,j]:malstern(i,j,m),
    print("Malstern-Tafel modulo ",m),
    genmatrix(ma,le,le)
)$

(%i57) Zstern(20);

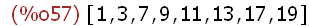
Für die Anzahl dieser Teilerfremden gibt es die Eulersche-Phi-Funktion

(%i58) eulerphi(m):=length(Zstern(m))$
eulerphi(20);

(%i60) malsterntafel(20);

(%i61) for i:6 thru 21 do print(malsterntafel(i))$

2.5 Potenztafeln

(%i62) /* Definition potenztafel(m) */
potenztafel(m):=block([le,Zs,hochstern],
    Zs:Zstern(m), le:length(Zs),
    hochstern(i,j,m):=(mod(Zs[j]^i,m)),
    array(ma,fixnum,le,le),
    for i:1 thru le do for j:1 thru le do ma[i,j]:hochstern(i,j,m),
    print("Potenz-Tafel von Zstern modulo ",m),
    print("Zstern(",m,") hat ",le," Elemente"),
    genmatrix(ma,le,le)
)$

(%i63) potenztafel(7);

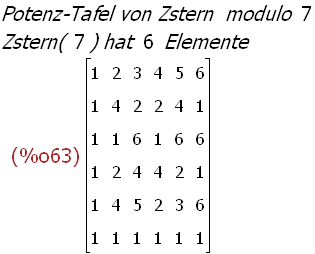
(%i64) for i:6 thru 21 do print(potenztafel(i))$

(%i65) potenztafel(30);potenztafel(31);

3 Ordnung eines Elementes, Powermod

3.1 Ordnung

Wenn man sich die Potenztafeln ansieht, fällt auf, dass alle
in der letzten Zeile ausschließlich 1 zeigen.
Das passt zu dem Satz der Gruppentheorie:
Element hoch Gruppenordnung =1
Die Gruppenordnung ist die Zahl der Elemente einer Gruppe.
Die Gruppen Zstern(m) haben eulerphi(m) Elemente

(%i67) Zstern(10); eulerphi(10);

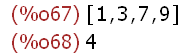
(%i69) Zstern(16); eulerphi(16);

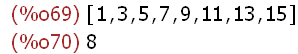
Man bildet den Begriff Ordnung eines Elementes:
ord(a)=k genau wenn k die kleinste Zahl mit a^k mod m =1 ist.
In den Potenztafeln ist k die Nummer der Zeile, in der zum ersten Mal
eine Eins in der k-Spalte auftaucht.

(%i71) makelist(mod(7^i,16),i,1,8);

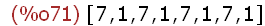
(%i72) makelist(mod(5^i,16),i,1,8);

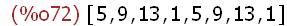
7 hat also in Zstern(16) die Ordnung 2, 5 hat die Ordnung 4

(%i73) ordo(a,m):=block([p,z],
                    p:a,z:1, while p>1 do (p:mod(a*p,m), z:z+1),
                    return(z)
                   );

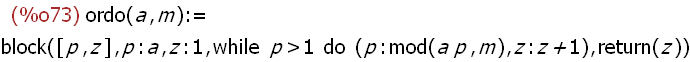
(%i74) ordo(13,16);

(%i75) makelist(mod(5^(4*n),16),n,1,10);

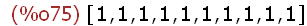
Man überlegt leicht, dass 5 hoch eine beliebiges 4-Vielfache
modulo 16 gleich 1 ist. Darum kann man 5^2010 mod 16 im Kopf ausrechnen.
5^2010=5^(2008+2) mod 16 = 5^2 mod 16=25 mod 16=9

(%i76) mod(5^2010,16);

Einweiter Satz der Gruppentheorie ist, dass dieElementordnung die
Gruppenordnung teilen muss. (Begründung bei "Nebenklassen".
Also kommen nur die Teiler von eulerphi als Elementordnungen infrage.

(%i77) potenztafel(18);

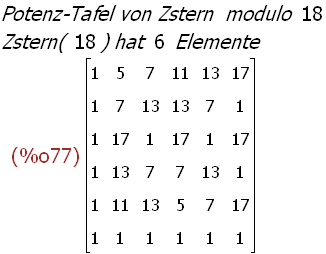
5 und 11 haben Ordnung 6, 7 und 13 haben Ordnung 3, 17 hat Ordnung2.

3.2 Powermod

Für die Kryptografie ist es wichtig, dass hohe Potenzen
riesiger Zahlen berechnet werden können.

(%i78) /*Definition von pmod(a.k.m) powermod*/
pmod(a,k,m):=block([x,i,pot],
    i:k, x:1,pot:a,
    marke,
    if mod(i,2)=1 then (x:mod(x*pot,m),
        if i=1 then return(x),
        i:i-1
    ),
    i:i/2,
    pot:mod(pot*pot,m),
    go(marke)
)$

(%i79) pmod(5,3,16);mod(5^3,16);

(%i81) pmod(12345,34567,16);mod(12345^34567,16);

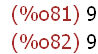
Die letzte Rechnung könnte man mit einem gewöhnlichen Taschenrechner
nicht ausführen. In der Kryptografie haben die Zahlen aber etwa
200 Stellen und nicht 5 wie oben. Dann geht der rechte Befehl auch nicht mehr.

(%i83) primlistebis(n):=([i,li],li:[],for i from 1 thru n do if primep(i) then li:append(li,[i]),li);

(%i84) lll:primlistebis(500);

(%i85) primep(250348280129);

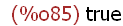
(%i86) makelist(pmod(99,p-1,p),p, primlistebis(500));

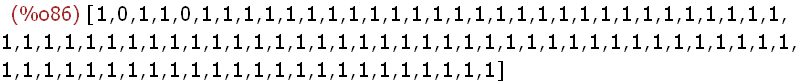
(%i87) mod(99^4998,4999);

3.3 Nebenklassen

In einer Gruppe Zstern(m) kann es Elemente geben, deren Potenzen
schon die ganze Gruppe erzeugen, nämlich die Elemente mit maximaler Ordnung.

(%i88) Zstern(18);

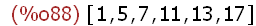
(%i89) makelist(mod(5^i,18),i,1,6);

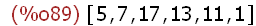
(%i90) pl[13]:makelist(mod(13^i,18),i,1,3);

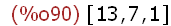
Die Elemente, die nicht in der Potenzenliste vorkommen, bilden
mit pl[13] echte Nebenklassen g*pl[a]

(%i91) mod(5*pl[13],18);mod(11*pl[13],18); mod(17*pl[13],18);

davon stimmen einige, hier sogar alle, überein.
Das Element der Ordnung 3 hat hier nur 2 Nebenklassen,
[13,7,1] und [5,11,17]
Alle Nebenklassen haben gleichviele Elemente, Anzahl ord(a)
Darum teilt die Elementordnung die Gruppenordnung.

Eulerscher Satz für Gruppen: Die Elemenordnung teilt die Gruppenordnung

(%i94) primep(250348280129);

(%i95) pmod(2,340,341); factor(341);

4 Betrachtungen für n=p q

4.1 Definitionen

4.2 Tafeln

(%i104) tafel(3,5);

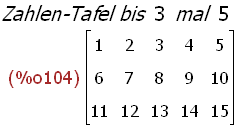
(%i105) p:3;q:5;tafel(p,q);modptafel(p,q); modqtafel(p,q);

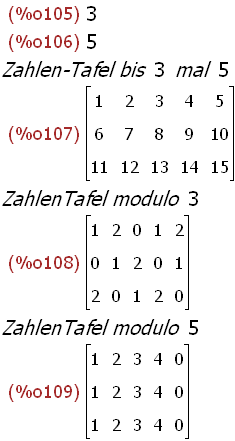
(%i110) p:5;q:7;tafel(p,q);modptafel(p,q); modqtafel(p,q);

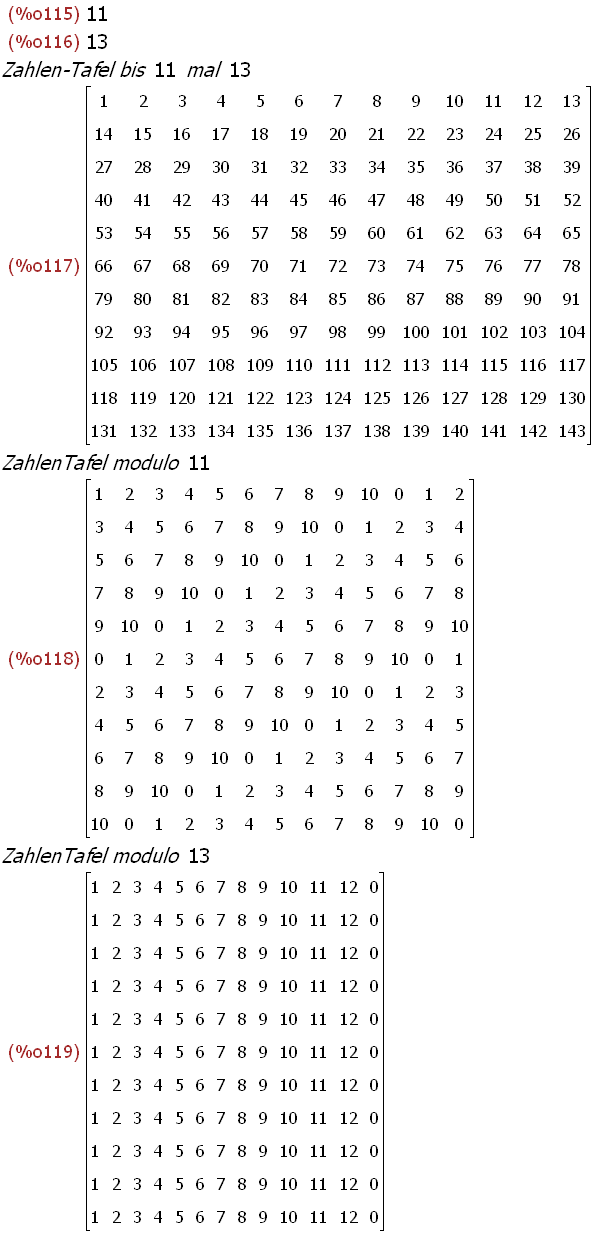
(%i115) p:11;q:13;tafel(p,q);modptafel(p,q); modqtafel(p,q);