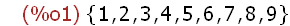
sets - how to Umgang mit Megen

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Okt 2010

1 Einleitung

Hier ist wenig in Deutsch ergänzt, da da meiste in die Datei
listen-folgen-mengen aufgommen ist, dort ausführlich in Deutsch erkärt

Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.

Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.

Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf,
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

2 Wie man mit Mengen umgeht (David Miller)

File: sets-how-to.wxm
Version: 1.0
Date: 20 January 2009
Author: David E. Miller

Purpose: How-to for using Maxima for creating and manipulating set objects.

Maxima Sets How-To

Abstract

This document comprises information and examples about the use Maxima set objects.
The examples are elementary in nature and serve merely to demonstrate the concepts.
This how-to is not comprehensive or exhaustive, however the most familiar basic set
concepts, relations, and operations are related to corresponding Maxima functions and
features. Definitions and concepts are intentionally informal and therefore not intended
to meet a rigorous standard.

Table of contents
1 Introduction
    1.1 Basic Set Terminology and Notation
    1.2 Maxima Set Basics
    1.3 Maxima Evaluation of Set Instances
2 Set Relations and Operations
    2.1 Relations Between Sets
    2.2 Set Operations
3 Odds and Ends
    3.1 Null Set Testing
    3.2 Making and Partitioning Sets
    3.3 Set Instance Iteration
4 Summary

1 1 Introduction

1 Introduction
Maxima may be used to define set objects and perform typical operations on defined
sets. The set objects must be defined by explicit enumeration. This means that the set
objects are defined using the ‘‘roster method'' as opposed to the ‘‘set-builder method''
in the terminology of sets. It is possible to ‘‘build up'' sets implicitly using Maxima
statements. Thus, in all cases the sets considered in this how-to are finite sets.

2 1.1 Basic Set Terminology and Notation

Definition. A set is a class of objects considered as an object itself.

Definition. The objects of a set are known as instances or elements of the set.

Note. Conceptually the objects that are instances of a set may be anything. A set must
be logically well-defined — that is, for any object it either is or is not an instance of the
set, and there exists a condition that determines which of these is true. Conceptual
oddities such as the set of all sets and so forth lead to contradictions and are of no
practical consequence in this context.

Notation. Sets are denoted as symbols for the instances of the set separated by
commas between curly brackets.

Example.

{a,e,i,o,u}
 {red, white, blue}
{2, 4, 6, 8}

Notation. Capital letters denote defined sets by convention. A proposition that an object
is or is not an instance of a set is denoted as a∈A or a∉A.

Example.

If A is defined as the set {1,3, 5,7,9}, then 1∈A is true and 2∈A is not true. The latter
may be expressed as 2∉A.

3 1.2 Maxima Set Basics

A Maxima set object is instantiated as follows.

Note: The form set(1,2,3,4,5,6,7,8,9) is equivalent:

(%i1) {1,2,3,4,5,6,7,8,9};

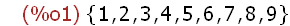
Set objects are named as in the following three examples:

(%i2) A:{1,2,3,4,5,6,7,8,9}$
B:{red,orange,yellow,green,blue,indigo,violet}$
C:{1,2,3,4,5,6,7,8,9,0,9,8,7,6,5,4,3,2,1}$
A;B;C;

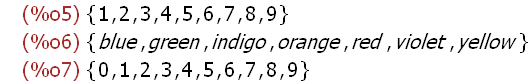
The name definition statements for set B and set C reveal that Maxima applies some set
simplification rules for redundant instances and may reorder the explicit listing.
Instances of a set that are identical are not considered to be different instances. Hence
these appear as a single instance in set C. The instances of set B are reordered
according to built-in Maxima rules.

Maxima provides flexibility in terms of the objects that may be instances of defined sets.
These objects may be Maxima names, list objects, other set objects and so forth. Even
Maxima expressions may instances of defined sets:

(%i8) (x:a/c + b/c, y:a/c + b/c, z:(a + b)/c)$
x;y;z;

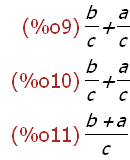
Here a Maxima block statement is used to name three expressions. Expressions x and y
are identical in form. Expression z is equivalent to x and y but not identical in form. Make
these names the instances of a set to see what results:

(%i12) {x,y,z};

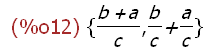
Since x, y , and z were assigned values in the form of expressions, Maxima evaluated
these names when used as instances of the above set. Although x and y are different
names, their values are the same. hence only one expression appears in the set. Note
that although z is equivalent to x and y it is a different expression in form and therefore
appears as a different instance of the set.

Maxima provides statements to test whether an object is an instance of a set or not:

(%i13) elementp(5,A);elementp(11,A);not(elementp(11,A));

So 5 is an instance of the set named A (5∈A is true), 11 is not an instance of set A (11∈
A is false), and so the negation of this statement is true — it is true that is is not the
case that 11 is an instance of set A (11∉A is true).

As was noted in the introduction, sets in Maxima are created explicitly as objects using
the equivalent of the ‘‘roster method'' of set definition. There is no direct way to define
a set using the ‘‘set-builder'' notation of the form:{x∈U|P(x) is true}, where U is the
so-called universal set (or universe of discourse), x is any instance of set U, and P(x) is a
condition that is true for x. However, it is possible to to do this in effect by using Maxima
statements to define a function in a way that has similar results:

(%i16) evens(S):=(E:{}, for e in S do (if evenp(e) then E:adjoin(e,E)),E)$
odds(S):=(O:{}, for e in S do (if oddp(e) then O:adjoin(e,O)),O)$
evens(A);odds(A);

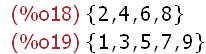
The two statements above that are used to define two Maxima functions (evens(S) and
odds(S)) use a block to group several statement together. First, a local name of a set (E
or O) is given the value of a null set { } (or ∅). This provides an empty set to use to
build a set. Then a test is made for each instance (e) of set A to determine if it is an
even or odd number. This serves the purpose of the P(x) of the set-builder notation.
Those instances that ‘‘pass'' the test, are included in the set of even or odd numbers
as the case may be by using the adjoin(e,E) or adjoin(e,O) operation. Other ways to
make sets using different Maxima statements are detailed in later section.

4 1.3 Maxima Evaluation of Set Instances

As noted above Maxima will evaluate names that appear as instances in the definition of
a set object. Thus, if a name x has an assigned value other than itself (the default value
of any name is itself), then this is the value that will appear in the set, and not the
name. The set B above was defined as a simple list of color names. If these names are
now assigned values note the results.

(%i20) B;

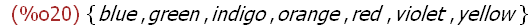
(%i21) red:1$orange:2$yellow:3$green:4$blue:5$indigo:6$violet:7$

The names that are the instances of set B are assigned the values 1 to 7 in the order listed
above. The set B displays the following instances:

(%i28) B;

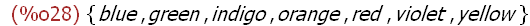
This may seem surprising, but this is the way Maxima behaves. At the time that set B was
defined the names that are the instances of this set had no values. Hences this is what
Maxima ‘‘remembers'' as the instances of set B — the names. However, subsequent to
this definition of set B the names that are instances of the set were assigned number
values 1 to 7. In order for set B to reflect these values an explicit evaluation of B is
required:

(%i29) ''B;

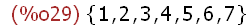
The two single quotes prefixed to the set name B forced an evaluation of the instances
of the set. On the other hand, if the values of the names of the instances of a set are
assigned prior to the set definition, then the evaluation takes place when the set is
defined. This can be seen by redefining set B here and seeing the displayed results:

(%i30) B:{red,orange,yellow,green,blue,indigo,violet}$
B;

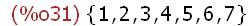
Note that the two single quotes prefixed to B were not required this time. This is
because B was redefined after the values for the names that are instances of B were
assigned. Thus the evaluation of these names occurred when set B was redefined
above.

This is a general rule. Evaluation of the instances of a set takes place when the set is
defined. If instances of a set are assigned values subsequent to the set definition,
evaluation of the instances of the set has to be explicitly forced on the set — as shown
above for example.

5 2 Set Relations and Operations

6 2.1 Relations Between Sets

Equality of sets is determined in the following way. First, define four sets to compare:

(%i32) S:{1,2,3,4,5,6,7,8,9}$
A:odds(S)$B:evens(S)$C:S$

Which sets are equal?

(%i36) is(A=B);is(C=S);

This result occurs because set A is the odd numbers of set S and set B is the even
numbers of set S and therefore not equal. Set C was assigned the same set as set S
and therefore equal.

(%i38) is(not A=B);

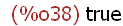
This is the same as the statement ‘‘is A≠B'' in mathematical notation.

(%i39) is(not C=S);

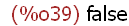
This is false because set C and set S are equal. Two sets may have the same cardinality
or not:

(%i40) S;A;ev(A);

(%i43) D:{11,12,13,14,15,16,17,18,19}$
is(D=S);
is(cardinality(D)=cardinality(''S));
is(cardinality(D)=cardinality(''A));

Sets D and S have the same number of elements — that is, they have a one-to-one
correspondence relation with each other even though the instances of each set are not
the same. Sets D and A are not in one-to one correspondence with each other even
though they have some elements in common. A Maxima function makes this easier to
use:

(%i47) onetoone(A,B):=is(cardinality(''A)=cardinality(''B))$
onetoone(D,S);onetoone(D,A);

This form is easier to use than having to type the full expression each time.

Sets that are not equal may be related by the fact that one set may be a subset
of another set.

(%i50) ''A;S;

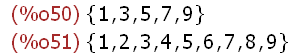
(%i52) subsetp(''A,S);
subsetp(D,S);

These are equivalent to the statement A⊂S and D⊂S.

Two sets may also be disjoint — having no elements in common.

(%i54) S;D;disjointp(S,D);
S;A;B;disjointp(S,''A);disjointp(''A,''B);

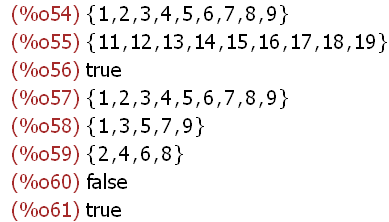
Set D is not a subset of set S and is therefore disjoint. Sets A and B are both subsets of
set S and therefore not disjoint. Maxima will also display well known relations between
special cases:

(%i62) subsetp(S,{});
subsetp({},S);
subsetp(S,S);
subsetp({},{});

No set is a subset of the null set except the null set itself. A set is a subset of itself. The
null set is a subset of every set.

7 2.2 Set Operations

Sets may be used to define other sets using the conventional set operations of
Maxima:Two sets may be combined according to common elements. The union of two
sets may be defined (the symbol ≜ means ‘‘equal by definition) as:

A∪B≜{x∈U| x∈A or x∈B}

(%i66) A:{1,2,3,4,5,6,7,8,9,10}$B:{11,12,13,14,15,16,17,18,19,20}$
union(A,B);

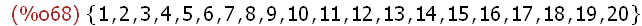
The union function may be used in a more general way having multiple sets as
arguments as in union(A,B,C,D,...). The intersection of two sets may defined as:

A∪B≜{x∈U| x∈A and x∈B}

(%i69) A:{1,2,3,4,5,6,7,8,9,10}$B:{6,7,8,9,10,11,12,13,14,15}$
intersection(A,B);

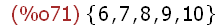
The intersection function may be used in a more general way having multiple sets as
arguments as in intersection(A,B,C,D,...).

The difference of two sets may be defined as follows:

A-B≜{x∈U| x∈A and x∉B}

(%i72) setdifference(A,B);
setdifference(A,A);

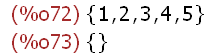
The setdifference function may be used to find the the complement of a set with respect
to a defined universal set. If set U is defined to be the universal set and set A is a
subset if U, then the complement of set A is denoted as A' (or ∼A) and is instantiated by
the following Maxima commands:

(%i74) U:{1,2,3,4,5,6,7,8,9,10,11,12}$A:{4,5,6,7}$
complement(U,A):=setdifference(U,A)$
complement(U,A);

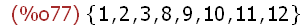
The function complement was defined here for convenience to emphasize the context in
which the setdifference function is used.

The Cartesian product of two sets may be defined as follows:

A×B≜{(x,y)| x∈A and y∈B}

Thus A×B is a set of ordered pairs. Maxima has no object type for ordered pairs. The
list object [x,y] is used instead for this purpose.

(%i78) A:{1,2,3,4}$B:{5,6,7,8}$
cartesian_product(A,B);
cartesian_product(A,A);

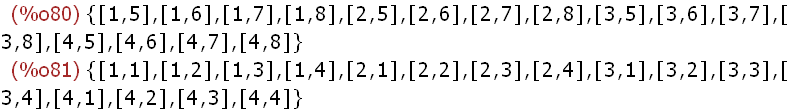
A power set is a set of all the subsets of a set.

Example:
 
S≜{♠, ♥, ♣, ♦}

This is a well-defined set and it has only four instances. A set with n instances defines
2 to the power of n subsets. So S has 2 to the 4th power or 16 possible subsets, and
so it is practical in this case to list the instances of the power set of S as:

{∅,{ ♠},{ ♥}, {♣}, {♦},{♠♥},{♠♣},{♠♦},{♥♣},{♥♦},
{♣♦},{♠♥♣},{♠♣♦},{♠♥ ♣♦}, {♥ ♣ ♦},S}

(%i82) powerset(''A);powerset(''B);

The distinct permutations of a set is obtained in the form of a set of list objects with
each list being a distinct ordering as follows:

(%i84) A:{hearts,clubs,spades,diamonds}$
B:permutations(A);
is(cardinality(B)=cardinality(A)!);

Hence this example verifies the fact that the number of permutations of n objects is n!
where n=4 and n!=24 in this case.

8 3 Odds and Ends

Maxima provides other set related features that fall into various categories.

9 3.1 Null Set Testing

A set may be tested to determine if it is null.

(%i87) A:{"not null"}$B:{}$
emptyp(A);emptyp(B);

10 3.2 Making and Partitioning Sets

Several methods are available to make sets. The set of numbers that are the of divisors
of a number is instantiated as follows:

(%i91) divisors(1024);divisors(941);

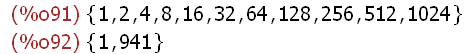
Since the only divisors of 941 are itself and 1, the result above indicates that 941 is a
prime number. Another method uses the makeset(expr,x,s) function.

(%i93) S:{[1,2],[3,4],[5,6],[7,8]}$
makeset([n/d],[n,d],S);

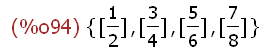
The makeset(expr,x,s) function requires an expression as a list that is to be formed in
the resulting set. Here expr is the list object [n/d]. The argument x is a list of the
variables used in the expr argument and forms a pattern for the set argument s which is
a set of list objects with a structure that matches the pattern. Here the pattern is [n,d]
and S is defined as a set of list objects having values matching this pattern. The result
is a set of list objects that have the value specified by expr. In this case a set of four
fractions were instantiated as list objects.

Another way to create a set from another set is to use the subset function:

(%i95) S:{1,2,3,4,5,6,7,8,9,10}$
subset(S,evenp);subset(S,oddp);

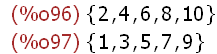
The subset command requires a set as an argument together with a predicate
(condition) that is evaluated for each member of the set S. In the example above, the
set S is the numerals 1 to 10 and the predicates are evenp and oddp resulting in the
two sets shown — one set of even numerals and one set of odd numerals of set S. The
instances of set S that result in a true evaluation of the predicate used are included in
the resulting set. The effect of applying these two subset functions to the set S
partitions that set into two sets — even and odd numerals. The partition_set function
will provide the same result using a single statement:

(%i98) partition_set(S,evenp);partition_set(S,oddp);

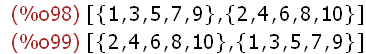
The above displays in two different lists but similar results. The first statement as
partition_set(S,evenp) results in a list objects of two set objects. The first is a set of the
instances of set S that are not even numerals. The second is the set that are even
numerals. Since the second statement uses oddp instead of evenp the result is
reversed.

11 3.3 Set Instance Iteration

There are two ways to to iterate using the instances of a set. The map function is the
easiest as in the following example:

(%i100) f(x):=x^2$
map(f,S);

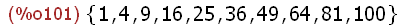
The function f(x) was defined as the square of x. The map(f,S) statement applied each
instance of set S as an argument x of function f resulting in a set of perfect squares.
The second method of iteration uses the for x in s do statement:

(%i102) for s in S do print (concat(s," ",f(s)));

In this example each instance of set S is assigned to s and then is printed along with
f(s) creating a small listing of the square of the numerals 1 to 10.

12 4 Summary

The above examples and explanation of set provisions does not exhaust all the features
of Maxima applicable to set objects. There is enough demonstrated here that is useful
to for most common purposes. The reader is directed to the Maxima documentation
related to set objects and related topics for more information and examples.

(%i103) "Bye!"$