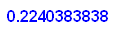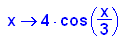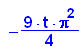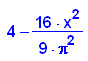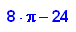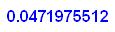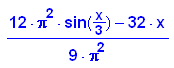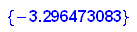Übung Analysis Jan 05
Mathematik mit MuPAD
Prof. Dr. Dörte Haftendorn Jan 05 haftendorn.uni-lueneburg.de/mathe-lehramt
a) Zeichnen Sie begründet einen Graphen von f mit f(x)=4 cos(x/3)
und integrieren Sie zwischen den beiden Nullstellen,
die dem Ursprung am nächsten sind.

• f:=x->4*cos(x/3)

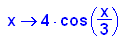
• plotfunc2d(cos(x),cos(x/3),f(x))

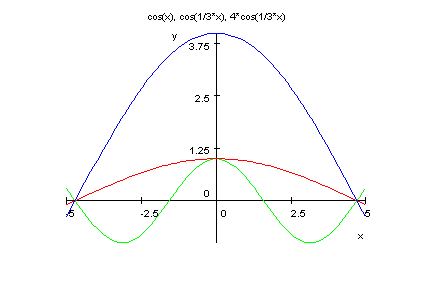
Integral,
Nullstellen sind das 3-fach der cos-Nullstellen

• int(f(x), x)

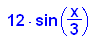
Wegen der Symmetrie kann man rechts allein rechnen.

• fl_echt:=2*int(f(x), x=0..3*PI/2)

• delete t:

Gesuchte Parabel, t noch unbekannt

• p:=x->t*(x-3*PI/2)*(x+3*PI/2)

• p(0)

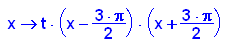
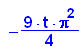
Das muss 4 werden:

• solve(p(0)=4,t)

• t:=op(%)

• p(x)

• expand(%)

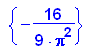
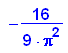
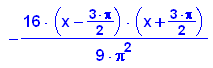
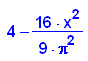
Das ist die gesuchte Parabel

• plotfunc2d(p(x),f(x),x=-5..7)

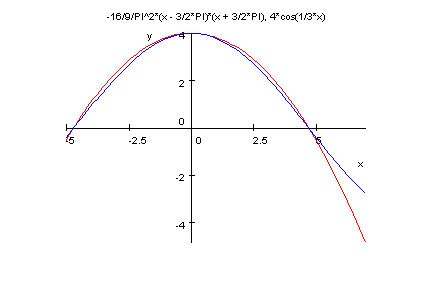
Rechts sieht man, dass der cos- blau
und die Parabel rot ist.

• int(p(x),x)

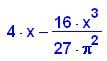
• fl_parabel:=2*int(p(x),x=0..3*PI/2)

• di:=fl_parabel-fl_echt;
  float(di);float(di/fl_echt);

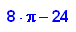
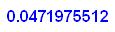
Also macht man einen Fehler von knapp 5%, wenn
man statt f die Parabel integriert.
-----------------------------------------------------------------
Abstandsfunktion:

• h:=x->p(x)-f(x)

• plotfunc2d(h(x))

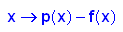
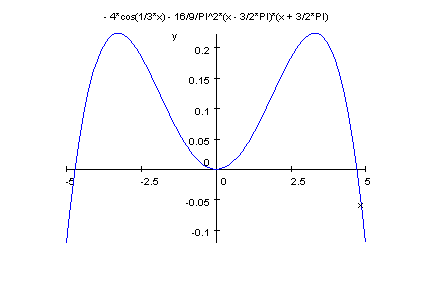
Symmetrisch und wie auch sonst wie erwartet.

• diff(h(x), x)

• hh:=simplify(%)

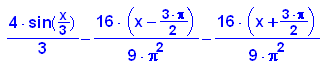
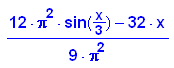
Transzendente Gleichung, nur numerisch lösbar.

• numeric::solve(hh=0,x)

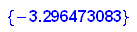
Das ist die Max-Stelle, das Abstandsmaximum ist:

• abstand:=float(h(op(%)))