m:=[214,122,94,61];
k:=[40,26,19,13];
lgm:=float(map(m,lg));
lgk:=float(map(k,lg));
![]()
![]()
![]()
![]()
Boxdimension
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Update Jan 08
https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
lg:=x->log(10,x):
Nikolaushaus
Methode 1,
k= Anzahl der in der Länge getroffenen Pixel, ausgezählt
m=Anzahl der von dem Fraktal getroffenen Pixel
m:=[214,122,94,61];
k:=[40,26,19,13];
lgm:=float(map(m,lg));
lgk:=float(map(k,lg));
![]()
![]()
![]()
![]()
Direkt auftragen, gleich mit Regressonsgerade, (auch gut für Excel geeignet)
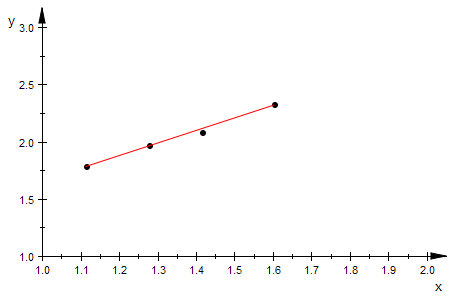
pktp:=plot::Scatterplot(lgk,lgm,ViewingBox= [1..2,1..3]);
plot(pktp)
![]()
Berechnung der Regresssionsgeraden
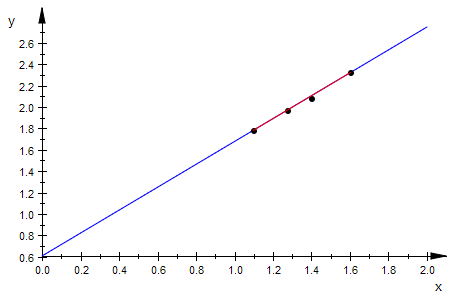
regger:=stats::linReg(lgk,lgm);
reggerade:=plot::Function2d(regger[1][2]*x+regger[1][1],x=0..2);
plot(reggerade,pktp)
![]()
![]()
Nikolaushaus
Methode 2,
k= Anzahl der in der Länge getroffenen Pixel,
Ausgerechnet aus Gesamterstreckung 600 Pixel und
Rasterweite w in Pixeln, wie sie auf meinen Blättern angeben ist.
m=Anzahl der von dem Fraktal getroffenen Pixel
m:=[214,122,94,61];
w:=[15,24,32,48];
k:=float([600/w[i] $ i=1..4]);
lgm:=float(map(m,lg));
lgk:=float(map(k,lg));
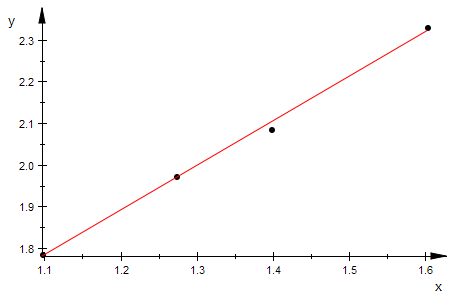
pktp:=plot::Scatterplot(lgk,lgm);
plot(pktp)
![]()
![]()
![]()
![]()
![]()
![]()
Berechnung der Regresssionsgeraden
regger:=stats::linReg(lgk,lgm);
regger[1][1]
![]()
![]()
Zusätzliche Zeichnung
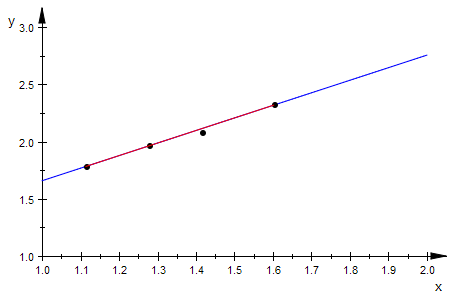
reggerade:=plot::Function2d(regger[1][2]*x+regger[1][1],x=0..2);
plot(reggerade,pktp)
![]()