f:=z->q*E^(2*PI*phi*I)*z
![]()
Sonnenblume
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Jan 08 Update 7.1.08
https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Erzeugung von Punkten durch komplexe Iteration
f:=z->q*E^(2*PI*phi*I)*z
![]()
phi:=(sqrt(5)-1)/2;float(%)
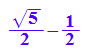
![]()
zu lesen als Anteil des Vollwinkels
gw:=phi*360;
g:=360-gw;
![]()
![]()
Dieser Winkel heißt goldener Winkel.
q:=0.999:
q bewirkt die passende Verkürzung.
n:=2:
li:=(f@@i)(1) $ i=1..n;
pkte:=[Re(li[j]),Im(li[j])] $j=1..n;
![]()
![]()
Die wirkliche Verwendung der Iteration ist ungünstig, weil die Berechnung von
Real- und Imaginärteil zu aufwendig ist. Man dreht mit der Uhr um 137,5... Grad.
Gerechnet math. positiv um 222,49... Grad.
phi:=(sqrt(5)-1)/2;
phi:=float(%)
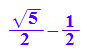
![]()
(1-phi)*55
![]()
Dazu noch mehr weiter unten.
phi:=float(sqrt(5)-1)/2;
n:=1000:
pkte:=[q^j*cos(2*PI*phi*j),q^j*sin(2*PI*phi*j)] $j=0..n:
plot(plot::Listplot([pkte],Axes=None,PointStyle=Squares,
Scaling=Constrained, LinesVisible=FALSE,PointSize=2))

############################################
Hier kann man mit Varianten experimentieren. 0.6 oder 0.62 oder 0.625
phivari:=0.615;
n:=1000:
pkte:=[q^j*cos(2*PI*phivari*j),q^j*sin(2*PI*phivari*j)] $j=0..n:
plot(plot::Listplot([pkte],Axes=None,PointStyle=Squares,
Scaling=Constrained, LinesVisible=FALSE,PointSize=2))
![]()

matrix([[i,(0.phivari*i*2)] $ i=1..13])

Hier für phivari=0.615, gibt es 13 Spiralen, nach je 16 Runden kommt
ein neues Karo in einen Spiralarm.
###############################################
Warum entstehen gerade 55 rechtsdrehende Spiralen?
phi:=float(sqrt(5)-1)/2
![]()
gw:=phi*360;
gw2:=360-gw
![]()
![]()
55*gw2/360
![]()
d.h. die 55 Spiralen kommen zustande, weil 55 goldene
Winkel sehr wenig mehr als 21 Runden ergeben.
Darum liegen die Karos nach je 21 Runden sehr dicht an den vorigen.
matrix([[i,(phi*i)] $ i=1..55])

Übrigens sind es gerade 34 linksdrehende Spiralen.