delete(Igel):
Igel:=plot::Turtle([Forward(15),Right(PI/4),Forward(10),Right(PI/2)
,Up,Forward(10),Down,
Forward(20)],LineColor=RGB::Red,LineWidth=1);
plot(Igel);
![]()

Fraktale mit MuPAD, Wegfraktale rekursiv
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, ( ehemals April 03) Update Apr. 11
https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
________________________________________________________________________________
LEVEL 1
Die Möglichkeiten in MuPAD 4 nochmal sind erheblich verbessert worden
(Woran ich nicht ganz unschuldig bin.) Somit ist nun ein LOGO-Ähnlichlicher Einstieg möglich,
den ich hier vorstellen werde, wenn ich mal wieder Zeit habe.
Kurz:
delete(Igel):
Igel:=plot::Turtle([Forward(15),Right(PI/4),Forward(10),Right(PI/2)
,Up,Forward(10),Down,
Forward(20)],LineColor=RGB::Red,LineWidth=1);
plot(Igel);
![]()

Das geht genauso wie in LOGO.
Igel::setLineColor(RGB::Blue):
Igel::left(300): Igel::forward(20): plot(Igel);
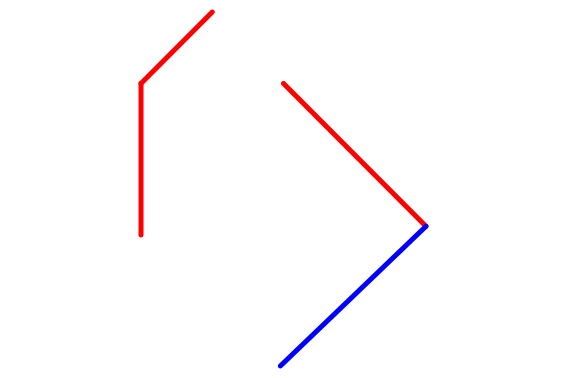
Dem Objekt Igel, das mit plot::Turtle(.....) definiert worden ist, können weitere
Befehle in seine Befehlsliste geschrieben werden. Diese werden dann klein
geschrieben Igel::forward statt Forward .
So kann man auch noch Farben umdefinieren. An die Strichdicke kommt man aber
nur bei der Definition des Objektes (was etwas schade ist).
LEVEL 2
Für Fraktale ist die einfache Befehlsliste nicht brauchbar, da geht nur das Anhängen
immer weiterer Befehle, bis das ganze Fraktal T entstanden ist.
Als Grundidee werden in Anlehnung an dieLindenmayersysteme einfacheProzeduren definiert:
delete x,w,T:
F:=proc(x) begin T::forward(x) end_proc:
f:=proc(x) begin T::penUp; T::forward(x); T::penDown; end_proc:
R:=proc(w) begin T::right(w)end_proc:
L:=proc(w) begin T::left(w)end_proc:
K:=proc() begin T::push() end_proc:
Z:=proc() begin T::pop() end_proc:
Rd:=proc() begin T::setLineColor([1,0,0]) end_proc:
Gr:=proc() begin T::setLineColor(RGB::Green) end_proc:
Bk:=proc() begin T::setLineColor(RGB::Black) end_proc:
Ma:=proc() begin T::setLineColor(RGB::Magenta)end_proc:
Eine rekursive Prozedur, d.h. eine, die sich selbst aufruft, bildet das Fraktal.
Der Initiator (Axiom) erscheint im Rekursionsanfang, in der Abbruchbedingung.
Der Generator wird ausgeschrieben, wobei der Prozedurname(n-1) anstelle von F( ) verwendet wird.
Die Weglänge muss in der Prozedur passend verkleinert werden.
################
Kochkurve
delete x,w,T:
koch:=proc(x,n) local a, w; begin
a:=x; w:=PI/3:
if n=0 then F(a): return() end_if;
a:=x/3;
koch(a,n-1):L(w):koch(a,n-1):R(w):R(w):
koch(a,n-1):L(w):koch(a,n-1):
end_proc:
T := plot::Turtle(LineWidth=1): /*die Turtle wird erzeugt*/
T::right(PI/2): /* Startrichtung rechts */
T::setLineColor([0.8,0.5,0]): /* Farben im RGB-System direkt*/
koch(200,1);
plot(T);
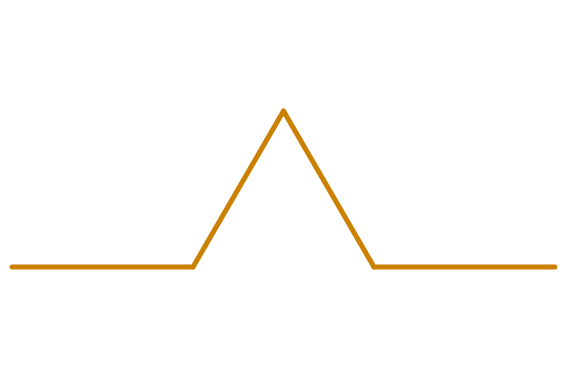
w:=PI/3:
T:= plot::Turtle(LineWidth=0.5): /*die Turtle wird erzeugt*/
T::right(PI/6): /* Startrichtung */
n:=4:
kx:=100:
Gr():koch(kx,n):R(w):R(w):Ma():
koch(kx,n):R(w):R(w):Rd(w):
koch(kx,n):R(w):R(w):
plot(T, Axes = None,Scaling=Constrained):

Zweig-Frakal
delete x,w,n,T:
zweig:=proc(x,w,n) local a; begin
a:=x:
if n=1 then F(x):return() end_if;
a:=a/3;
zweig(a,w,n-1):K():L(w):Rd():zweig(a,w,n-1):Gr():Z():
zweig(a,w,n-1):K():R(w):Bk():zweig(a,w,n-1):Gr():Z():
zweig(a,w,n-1):
end_proc:
Für die Umrechnung von Gradmaß in Bogenmaß nimmt man deg als Faktor
Deg:=PI/180:float([45*Deg,PI/4]) /* Winkel in Grad */
![]()
T:= plot::Turtle(LineColor=RGB::Green):zweig(1,43*Deg,3):
plot(T):
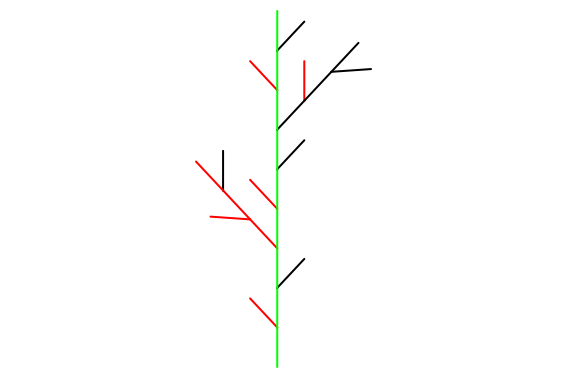
Der Vorteil gegenüber den Lindenmayersystemen ist, dass man auf die erzeugte Turtle zugreifen
und so mehrere Stufen in ein Bild stellen kann.
x:=27:w:=30*Deg: T := plot::Turtle(LineColor=RGB::Green):
n:=5:
K():zweig(x,w,1):Z():T::right(PI/2):T::forward(6):T::left(PI/2):
K():zweig(x,w,2):Z():T::right(PI/2):T::forward(8):T::left(PI/2):
K():zweig(x,w,3):Z():T::right(PI/2):T::forward(8):T::left(PI/2):
K():zweig(x,w,4):Z():T::right(PI/2):T::forward(10):T::left(PI/2):
zweig(x,w,5):
plot(T):
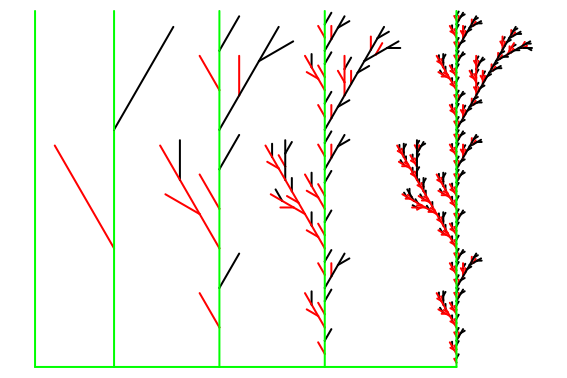
Ein weiterer Vorteil gegenüber den Lindenmayersystemen ist, dass man leichter verschiedene
Fraktale kombinieren und die Farben steuern kann. Auch die Parameter lassen sich von außen steuern.
delete x,w,n,T:
dolde:=proc(x,w,n) local a; begin
a:=x:
if n=1 then Ma(): F(a);return(): end_if;
a:=x/3; Gr():
zweig(a,w,n-1):
K():L(w):Ma():dolde(a,w,n-1):Gr():Z():
K(): Bk():dolde(a,w,n-1):Gr():Z():
K():R(w):Ma():dolde(a,w,n-1):Gr():Z():
end_proc:
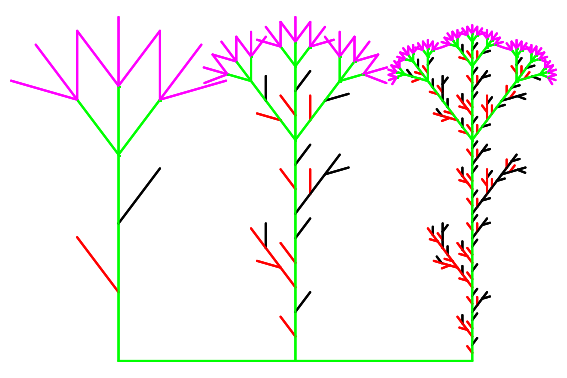
delete x,w,T,n;
T := plot::Turtle(LineColor=RGB::Green):
T::push():do3:=dolde(14,37*Deg,3):T::pop():
R(PI/2):f(4):L(PI/2):
T::push():do4:=dolde(15,37*Deg,4):T::pop():
R(PI/2):f(4):L(PI/2):
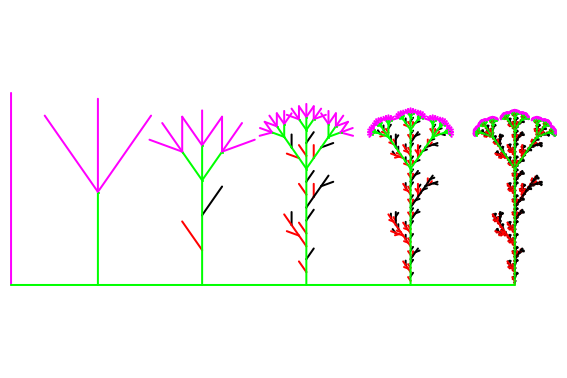
do5:=dolde(15,37*Deg,5):
plot(do3,do4,do5):
x:=40:w:=35*Deg:T := plot::Turtle(LineColor=RGB::Green, LineWidth=0.4):
K():dolde(x*0.55,w,1):Z():T::right(PI/2):T::forward(10):T::left(PI/2):
K():dolde(x*0.8,w,2):Z():T::right(PI/2):T::forward(12):T::left(PI/2):
K():dolde(x*0.9,w,3):Z():T::right(PI/2):T::forward(12):T::left(PI/2):
K():dolde(x,w,4):Z():T::right(PI/2):T::forward(12):T::left(PI/2):
K():dolde(x,w,5):Z():T::right(PI/2):T::forward(12):T::left(PI/2):
dolde(x,w,6):
plot(T):