kreis:=t->cos(t);
r:=t->kreis(t)+k;
![]()
![]()
Pascalsche Schnecken und ihre Inversion
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Aug. 07 Update 20.08.07
www.mathematik-verstehen.de https://mathe.web.leuphana.de
kreis:=t->cos(t);
r:=t->kreis(t)+k;
![]()
![]()
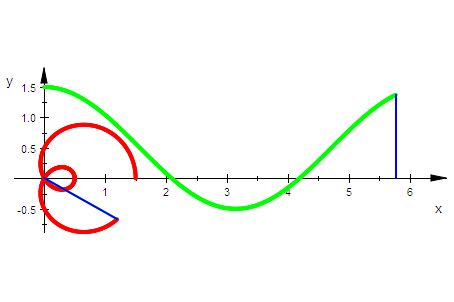
k:=0.5: //Leinenlänge
pascal:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
pkt:=plotPoint2d([r(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
leine:=plot::Line2d([r(t)*cos(t),r(t)*sin(t)],[kreis(t)*cos(t),kreis(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
pascalkart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
plot(pascal,radiusbetrag2,radius2,pascalkart,radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth);

einkreis:=t->1:
rinv:=t->1/(kreis(t)+k);
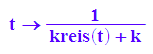
k:=0.5: //Leinenlänge
inv05:=plot::Polar([rinv(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,1], Mesh=400):
pkt:=plotPoint2d([rinv(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
invlinie:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.8, LineColor=[0,0,0]):
invlinie01:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[0,0],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
invlinie02:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
inv05kart:=plot::Curve2d([t,rinv(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[rinv(t)*cos(t),rinv(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(rinv(t))*cos(t),abs(rinv(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,rinv(t)],t=0..2*PI):
einkreisp:=plot::Polar([1,t],t=0..2*PI,
LineWidth=1,LineColor=[0,0,1], Mesh=200):
plot(einkreisp,inv05,radiusbetrag2,radius2,inv05kart,
radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth, ViewingBox=[-PI..2*PI, -PI..PI]);

plot(einkreisp,pascal,inv05,
invlinie,invlinie01,invlinie02,
ViewingBox=[-PI..2*PI, -PI..PI])
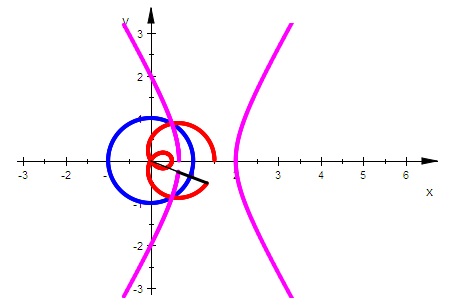

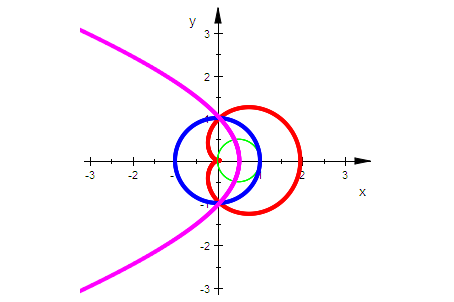
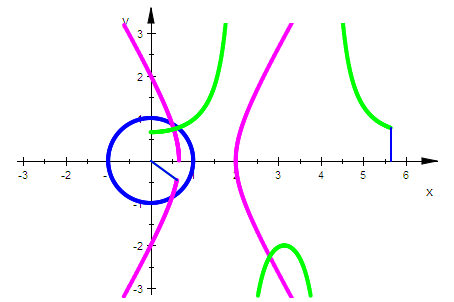
Das Inverse der Pascalschen Schnecken mit Schlaufen ist eine Hyperbel
Variation der Leinenlänge
k:=1.5: //Leinenlänge
pascal:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
pkt:=plotPoint2d([r(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
leine:=plot::Line2d([r(t)*cos(t),r(t)*sin(t)],[kreis(t)*cos(t),kreis(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
pascalkart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
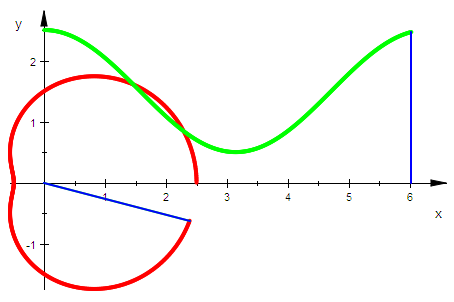
plot(pascal,radiusbetrag2,radius2,pascalkart,radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth);

einkreis:=t->1:
rinv:=t->1/(kreis(t)+k);
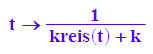
k:=1.5: //Leinenlänge
inv15:=plot::Polar([rinv(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,1], Mesh=400):
pkt:=plotPoint2d([rinv(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
invlinie:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.8, LineColor=[0,0,0]):
invlinie01:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[0,0],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
invlinie02:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
inv15kart:=plot::Curve2d([t,rinv(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[rinv(t)*cos(t),rinv(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(rinv(t))*cos(t),abs(rinv(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,rinv(t)],t=0..2*PI):
einkreisp:=plot::Polar([1,t],t=0..2*PI,
LineWidth=1,LineColor=[0,0,1], Mesh=200):
plot(einkreisp,inv15,radiusbetrag2,radius2,inv15kart,
radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth, ViewingBox=[-PI..2*PI, -PI..PI]);
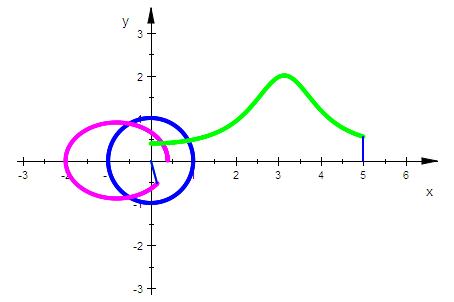

plot(einkreisp,pascal,inv15,
invlinie,invlinie01,invlinie02,
ViewingBox=[-PI..2*PI, -PI..PI])
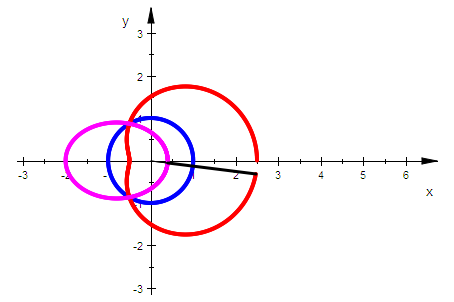

Das Inverse der stumpfen Pascalschen Schnecken ist eine Ellipse
#################
k:=1: //Leinenlänge
pascal:=plot::Polar([r(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
pkt:=plotPoint2d([r(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
leine:=plot::Line2d([r(t)*cos(t),r(t)*sin(t)],[kreis(t)*cos(t),kreis(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
pascalkart:=plot::Curve2d([t,r(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(r(t))*cos(t),abs(r(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,r(t)],t=0..2*PI):
plot(pascal,radiusbetrag2,radius2,pascalkart,radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth);

einkreis:=t->1:
rinv:=t->1/(kreis(t)+k);
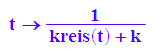
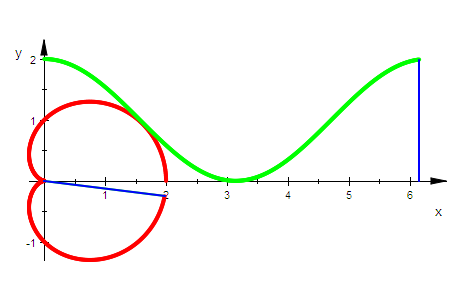
k:=1: //Leinenlänge Kardioide
inv1:=plot::Polar([rinv(t),t],t=0..ende,ende=0..2*PI,
LineWidth=1,LineColor=[1,0,1], Mesh=400):
pkt:=plotPoint2d([rinv(t),t],t=0..ende,ende=0..2*PI,PointSize=1.1):
invlinie:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.8, LineColor=[0,0,0]):
invlinie01:=plot::Line2d([rinv(t)*cos(t),rinv(t)*sin(t)],[0,0],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
invlinie02:=plot::Line2d([0,0],[r(t)*cos(t),r(t)*sin(t)],t=0..2*PI,
LineWidth=0.3, LineColor=[0,0,0]):
inv1kart:=plot::Curve2d([t,rinv(t)],t=0..ende,ende=0..2*PI,
LineWidth=1, Mesh=400, LineColor=RGB::Green):
radius2:=plot::Line2d([0,0],[rinv(t)*cos(t),rinv(t)*sin(t)],t=0..2*PI,
LineWidth=0.5):
radiusbetrag2:=plot::Line2d([0,0],[abs(rinv(t))*cos(t),abs(rinv(t))*sin(t)],
t=0..2*PI,LineColor=[0,1,0]):
radiusordi2:=plot::Line2d([t,0],[t,rinv(t)],t=0..2*PI):
einkreisp:=plot::Polar([1,t],t=0..2*PI,
LineWidth=1,LineColor=[0,0,1], Mesh=200):
plot(einkreisp,inv1,radiusbetrag2,radius2,inv1kart,
radiusordi2,LineWidth=0.5,
AnimationStyle=BackAndForth, ViewingBox=[-PI..2*PI, -PI..PI]);
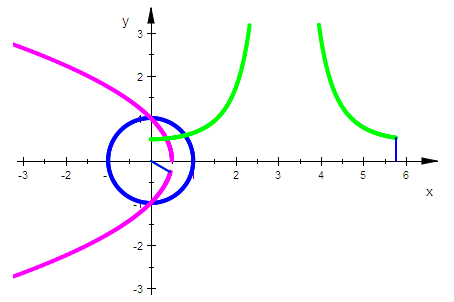

plot(einkreisp,pascal,inv1,
invlinie,invlinie01,invlinie02,
ViewingBox=[-PI..PI, -PI..PI])
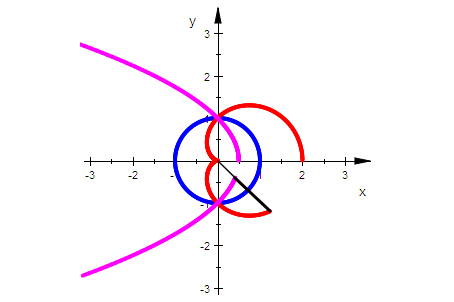

Das Inverse der Kardioide ist die Parabel
delete k,t
Animation der Pascalschen Schnecken und ihrer Inversen allein:
pascalk:=plot::Polar([r(t),t],t=0..2*PI,k=-1.5..1.5,
LineWidth=1,LineColor=[1,0,0], Mesh=400):
inv:=plot::Polar([rinv(t),t],t=0..2*PI,k=-1.5..1.5,
LineWidth=1,LineColor=[1,0,1], Mesh=400):
kreisg:=plot::Polar([r(t)|k=0,t],t=0..2*PI,
LineWidth=0.4,LineColor=[0,1,0], Mesh=400):
plot(pascalk,kreisg, einkreisp,inv,ViewingBox=[-PI..PI, -PI..PI])