Konstruierbare n-Ecke
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Jan. 06 Update 31.01.06
Es fehlen nocht textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Eine Fermat-Primzahl ist eine Primzahl der Gestalt 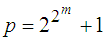
fermatZahlen:=2^(2^m) +1 $ m=0..4
![]()
factor(2^(2^m) +1) $ m=0..4
![]()
Diese ersten fünf Fermatschen Zahlen sind Primzahlen.
Die nächsten drei sind zerlegbar.
factor(2^(2^m) +1) $ m=5..7
![]()
Bis heute hat man keine weiteren Fermatschen Primzahlen gefunden.
Satz von Gauß: Das n-Eck mit n>2 ist genau dann konstruierbar,
wenn n eine Zweierpotenz ist oder sich schreiben lässt als
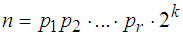
mit verschiedenen Fermat-Primzahlen pi
Gute Erklärungen und Ergänzungen in:
W. Henn: Elementare Algebra und Geometrie Vieweg 2003
ISBN 3-258-03201-4
Alle konstruierbaren n-Ecke mit n < 300
z:=(2^k $ k=2..8)
![]()
d:=(3*2^k $ k=0..6)
![]()
f:=(5*2^k $ k=0..5)
![]()
s:=(17*2^k $ k=0..4)
![]()
h:=257;
![]()
df:=(3*5*2^k $ k=0..4)
![]()
ds:=(3*17*2^k $ k=0..2)
![]()
fs:=(5*17*2^k $ k=0..1)
![]()
dfs:=(3*5*17*2^k $ k=0..0)
![]()
alle:=(z,d,f,s,h,df,ds,df):
alle:={alle}:
alle[1..10];alle[11..20];alle[21..30];alle[31..34];
![]()
![]()
![]()
![]()
Dies sind die 34 für alle mit Zirkel und Lineal konstruierbaren n-Ecke, n<300
matrix([sort([op(alle[1..17])]),sort([op(alle[18..34])])]);

Die nicht mit Zirkel und Lineal konstrierbaren n-Ecke mit n<300
stehen hier unten:
(gruppiert in nach Zehnern)
(nk[k]:={}:
for i from 10*(k-1) to 10*k-1 do
if not contains(alle,i) then nk[k]:=(nk[k] union {i})
end_if
end_for ) $ k=1..30:
nk

######################################################
quasi-konstruierbare n-Ecke
Dieter Riebesehl fand im Jan 06:
Das 7-Eck ist quasi-konstruierbar, d.h. mit Zirkel, Lineal und Parabellineal.
Der allgemeine Winkel ist drittelbar als Quasi-Konstruktion.
Damit ergibt sich eine Liste von quasi-konstruierbaren n-Ecken: n<300
sq:=(7*2^k $ k=0..5)
![]()
alle7q:=(alle union map(alle,_mult,7))union {sq} //Menge, keine Doppelten
![]()
gr300:=[i $ i=300..2000]:
alle7qs:=sort(listlib::setDifference([op(alle7q)], gr300))
![]()
Jetzt ist dieses noch mit allen Dreierpotenzen zu multiplizieren.
alle7qs:
(li[k]:=map(alle7qs,_mult,3^(k-1))) $ k=1..5:
alle73q:=(li[1].li[2].li[3].li[4].li[5]):
gr23000:=[i $ i=300..23000]:
alle73qk:=sort(listlib::setDifference(alle73q, gr23000));
nops(alle73qk);
![]()
![]()
matrix([sort([op(alle73qk[1..15])]),sort([op(alle73qk[16..30])])
,sort([op(alle73qk[31..45])]),sort([op(alle73qk[46..60])])
,sort([op(alle73qk[61..75])])]);

Hier stehen streng- oder wenigstens quasi-konstruierbare n-Ecke. n<300
Es sind 75 n-Ecke.
Es könnte aber noch weitere quasi-konstruierbare n-Ecke geben
+++++++++
Die noch nicht erfassten n-Ecke sind die unten folgenen.
Darunter könnten noch weitere quasi-konstruierbare n-Ecke sein.
Eingearbeitet sind nur die von 3 und 7 "abstammenden Konstuktionen".
(nkq[k]:={}:
for i from 10*(k-1) to 10*k-1 do
if not contains({op(alle73qk)},i) then nkq[k]:=(nkq[k] union {i})
end_if
end_for ) $ k=1..30:
nkq
