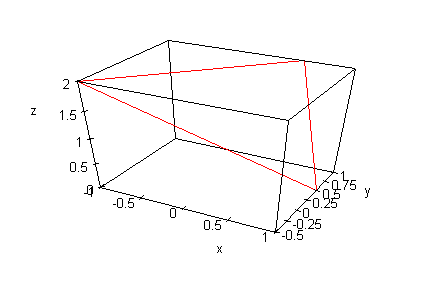
Zentralprojektion Geometrie mit MuPAD, Elliptische Geometrie, passend zu Cinderella Prof. Dr. Dörte Haftendorn 07.07.04 Version vom 07.07.04

Kugel, !!! alle Graphen im 3-D-Viewer ansehen!!!!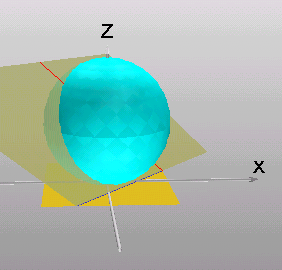

• ku := plot::Surface3d(
    [cos(u)*cos(v), sin(u)*cos(v),sin(v)+1], u = 0..2*PI, v = 0..2*PI);
  plot(ku)

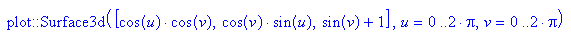
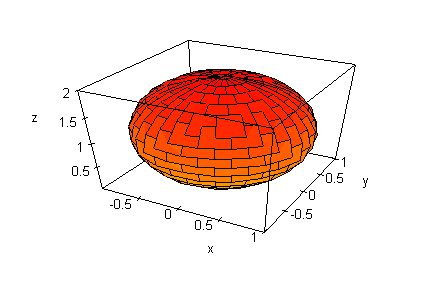
• grund := plot::Surface3d(
    [u,v,0], u = -1..1, v = -1..1):
  

• pkt:=[1,0.5,0]:

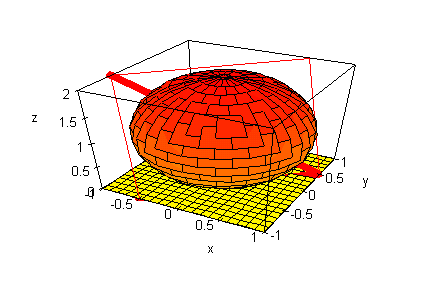
Die Gerade durch den Ur-Punkt und den Kugelmittelpunkt scheidet die Kugel im dem Bildpunkte-Paar.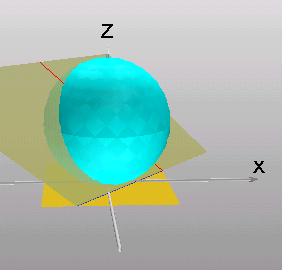

• ger := plot::line(
    pkt,[-1 ,-0.5,2],LineWidth=50):
  plot(grund,ku,ger)

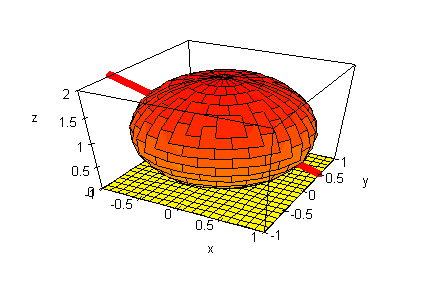
Bild einer Geraden ist ein Großkreis. Er ist Schnitt der Ebene durch die Gerade und den Kugelmittelpunkt mit der Kugel.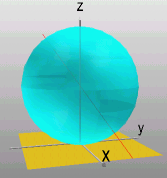

• x0:=1:y0:=0.5:x1:=-0.5:y1:=-1:

• ebb:=plot::Surface3d([r*(x0-x1)+s*x0,r*(y0-y1)+s*y0,1-s],r=-1..0.7,s=-1..1):

• gerade := plot::line(
    pkt,[-0.5 ,-1,0],LineWidth=50):
  plot(grund,ku,ger,gerade,ebb)

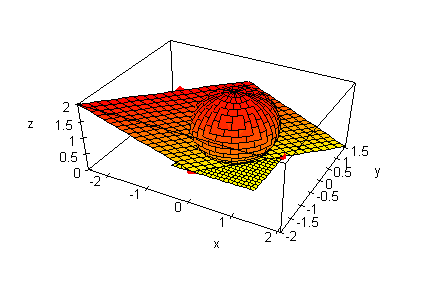
Polygone werden in 3D nicht gefüllt. Daher klappte dei Polygonidee nicht.

• ebene:= plot::Polygon::convert(
  polygon(point(1,0.5,0),point(-0.5,-1,0),point(-1,-0.5,2),
  point(0.5,1,2),point(1,0.5,0))):
  //auch Dreiecke wurden nicht gefüllt.
  ebene1 := plot::Polygon::convert(
  polygon(point(1,0.5,0),point(-0.5,-1,0),point(-1,-0.5,2),point(1,0.5,0),Filled=TRUE)):
  ebene2 := plot::Polygon::convert(
  polygon(point(1,0.5,0),point(-1,-0.5,2),
  point(0.5,1,2),point(1,0.5,0),Filled=TRUE)):
  plot(grund,ku,ger,gerade,ebene)  

• ee:=plot::Polygon::convert(polygon(point(1,0.5,0),point(-1,-0.5,2),
  point(0.5,1,2),point(1,0.5,0)),Filled=TRUE):plot(ee)