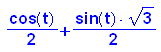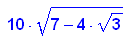Gleichseitiges Dreieck im Quadrat
Prof. Dr. Dörte Haftendorn, 12/04

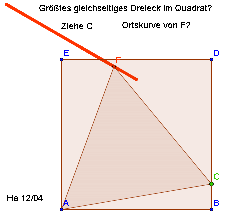
AB=10
C hat in Polarkoordinaten die Darstellung r=10/cos(t).
Die Spitze P des Dreiecks hat einen Polarwinkel, der um 60°=PI/3
größer ist.
Also ist die Polardarstellung von P r=10 / cos(t-PI/3)

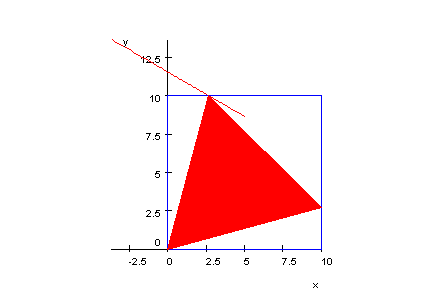
• gr:= plot::polar([ 10/cos(t-PI/3),t], t = [PI/3,PI/3+PI/4], 
  Grid = [100]):
  quad:=plot::Polygon(plot::Point(10,0),plot::Point(10,10),
  plot::Point(0,10),plot::Point(0,0),Color=[0,0,1],Closed=TRUE):
  drei:=plot::Polygon(plot::Point(0,0),plot::Point(10,0),
  plot::Point(5,5*sqrt(3)),Closed=TRUE, Filled=TRUE,Color=[1,0,0]):
  plot(gr,quad,drei,Scaling=Constrained):

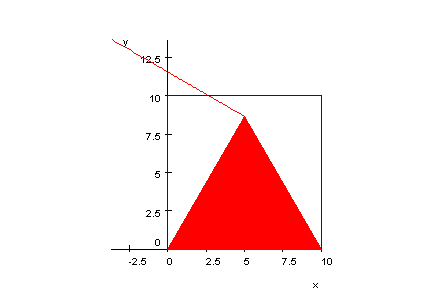
Die Ortskurve von P ist also eine Gerade.
"Also" zunächst nach "Sicht".
Allemeine Gerade y=m x + b in Polarkoordinaten:
x=r cos(t), y=r sin(t) ergibt r(sin(t)- m cos(t))=b.
Bedenkt man die Additionstheoreme

• expand(cos(t-PI/3))

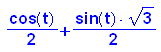
so sieht man

• b:=20/sqrt(3):m:=-1/sqrt(3):plotfunc2d(m*x + b,10)

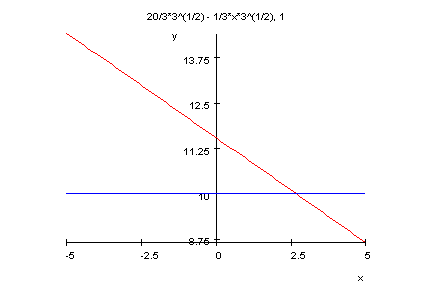
Es ist also die Ortskurve wirklich eine Gerade.
Nun ist noch zu bestimmen, wo diese Gerade die 10 erreicht:

• s:=expand(op(solve(m*x+b=10,x)))

• float(s)

Lage von C in dieser Stellung

• rmax:=simplify(sqrt(10^2+s^2))

• v:=sqrt(rmax^2-10^2)

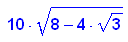
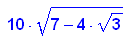
Das soll s sein?!?!?!?!?

• float(%)

• v^2

• expand(s^2)

Ja, das größte Dreiecks hat natürlich eine symmetrische Lage.
Bei Wurzeln kann man sich immer nur wundern.

• gr:= plot::polar([ 10/cos(t-PI/3),t], t = [PI/3,PI/3+PI/4], 
  Grid = [100]):
  quad:=plot::Polygon(plot::Point(10,0),plot::Point(10,10),
  plot::Point(0,10),plot::Point(0,0),Color=[0,0,1],Closed=TRUE):
  dreimax:=plot::Polygon(plot::Point(0,0),plot::Point(10,s),
  plot::Point(s,10),Closed=TRUE, Filled=TRUE,Color=[1,0,0]):
  plot(gr,quad,dreimax,Scaling=Constrained):