Winkeldreiteilung-Versuch nach Sch.
Autor der Konstruktion ist mir bekannt, da sie aber falsch ist, nenne ich ihn hier nicht.
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02, Feb.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
####################################################################
GeoGebra.Datei Winkeldritt-sch-ggb
hb:=x->tan(t)*(x+1);
a:=x->tan(s)*x;
ca:=x->tan(s-2*t)*(x+cos(s))-sin(s);
![]()
![]()
![]()
s ist der Steigungswinkel der Geraden OF, die oben blau und unten rot ist, Sie heißt a.
t ist der Steigungswinkel der Geraden HB (Name hb), die unten blau ist. t wird unten Parameter sein.
Aus dem Umfangswinkelsatz folgt, dass der Steigungswinkel der Geraden CA (Name ca), die unten grün ist,
dann s-2t ist. Als Kreis ist hier der Einheitskreis genommen.
Gesucht ist der Winkel s/3.
Der Schnittpunkt der grünen und der blauen Geraden heiße P.
Der Steigungswinkel der Geraden OP soll der gesuchte Drittelwinkel sein.
Dass das nicht der Fall ist, wird schon durch das Gegenbeispiel mit GeoGebra bewiesen,
denn das Doppelte von 25.77 ist 51,54 und nicht 51.89.
Im Folgenden wird es nochmals analytisch gezeigt, warum man mit Zeichnungen
von Hand ohne Einsatz von Mathematik zu der Meinung, es handele sich um eine Winkeldrittelung,
kommen konnte.
s:=1;plotfunc2d(hb|t=0.2,a,ca|t=0.1,x=-1.5..1.5,
Scaling=Constrained)
![]()
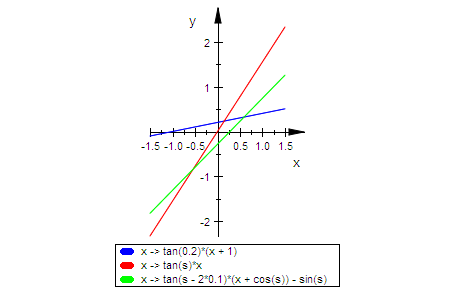
Bestimmung von P
delete s;
solve(hb(x)=ca(x),x)
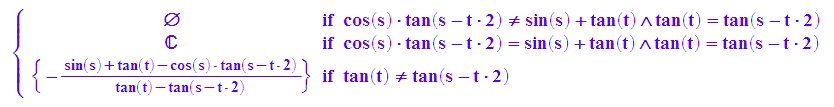
In den geschweiften Klammern ist x(t) für P. y(t)=tan(s)*x(t) folgt aus Gerade a
Im Folgenden sind mit dieser Parameterdarstellung die Ortskurven von P
für verschiedene s gezeichnet.
cur1:=plot::Curve2d([-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)),tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1)]|s=1,t=-2..2):
cur2:=plot::Curve2d([-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)),tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1)]|s=0.7,t=-1.5..2, LineColor=[1,0,0]):
cur3:=plot::Curve2d([-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)),tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1)]|s=0.4,t=-1.5..2, LineColor=[0,1,0]):
plot(cur1, cur2,cur3,ViewingBoxXRange=-3..5)
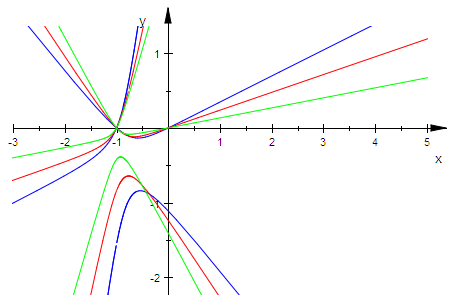
Es zeigt sich, dass die Ortskurven keine Geraden sind, im Bereich von 0 bis 1, der hier
interessiert sind sie einigermaßen gerade, aber nicht wirklich.
Die Konstruktion beruht darauf, dass man für jedes vorgegebene s und für beliebiges t
( mit 0<t<s/6 ) ein P erhält, das den Winkel s/3 erzeugt.
ger:= ((tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1))/(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)) )|{s=1,t=0.01}) *x:
gerade:=plot::Function2d(ger,x=0..8, LineColor=[1,0,1]):
kreis:=plot::Curve2d([cos(t),sin(t)],t=0..1,LineColor=[1,0.5,0]):
drittelger:=plot::Function2d(1/3*x,x=0..8, LineColor=[1,0,0]):
plot(cur1,gerade,kreis, drittelger);
plot(cur1,gerade,kreis, drittelger, ViewingBox=[0.94..0.95, 0.3..0.33]);
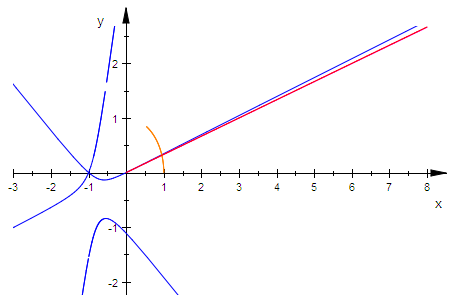
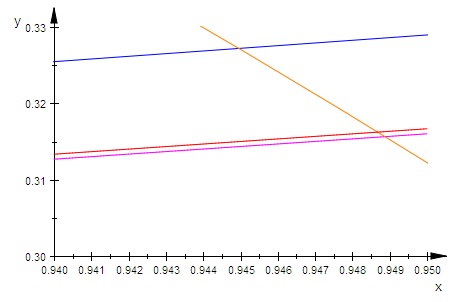
Dies zeigt, dass die wahre Drittelgerade(rot), die von einem bestimmtem
Punkt P (s=1, t=0.01) lila erzeugte Geade und die zugehörige Ortskurve den Einheitskreis
an ganz verschiedenen Stellen schneiden.
Also ist die Konstruktion falsch.
--------------------
Das zeigt sich auch numerisch an einem naheliegenderen Beispiel:
DIGITS:=30:
erg:=float([-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)),tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1)]|{s=1,t=0.1})
![]()
Dies ist der Punkt P, es folgt sein Steigungswinkel und der Sollwert.
float(arctan(erg[2]/erg[1]));float(1/3)
![]()
![]()
Dies stimmt nicht überein.
------------------------------------------
Mit dem Umfangswinkelsatz kann man überlegen, dass für s= 1 und t=1/6
2t = s/3 ist. Darum ist dies der einzige Fall, in dem P den richtigen Wert liefert. Das ist aber
der Fall, wenn die Konstruktion versagt, weil nämlich P auf dem Kreis selbst liegt,
Diesen Grenzfall kann man also nicht mit Zirkel und Lineal konstruieren.
erg:=float([-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t)),tan(t)*(-1/(tan(t) - tan(s - 2*t))*(sin(s) + tan(t) - cos(s)*tan(s - 2*t))+1)]|{s=1,t=1/6});
float(arctan(erg[2]/erg[1]));float(1/3)
![]()
![]()
![]()
Es war übrigens von vornherein klar, dass die Winkeldrittelung mit Zirkel und Lineal nicht
konstruierbar ist (siehe meine Internetseiten), das ist BEWIESEN !!!!!!!!. Seit 200 Jahren mindestens.
Ein Beweis ist kein Glaubenssatz. Wenn für eine Aussage kein Beweis gefunden wurde,
heißt die Aussage "Vermutung". Bei der Unmöglichkeit der konstruktiven Winkeldreiteilung handelt es sich
nicht um eine !!!!!! Vermutung, sondern einen bewiesenen mathematischen Satz.