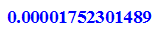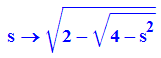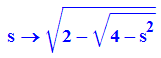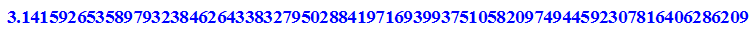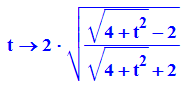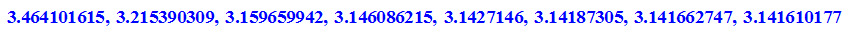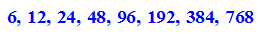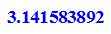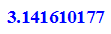Einschachtelung von PI durch innere und äußere n-Ecke
Prof. Dr. Dörte Haftendorn, Jan 05 www.uni-lueneburg.de/mathe-lehramt
Diese Datei ist für die Dreiecks-Familie durchgeführt, funktioniert aber auch für die Vierecksfamilie.
n und die Startseiten für innen und außen sind dann neu einzutragen.
Danach reicht "Notebook->Evaluiere->alle Eingaben"

Version 3-Eck
Es geht um n-Ecke innen und aussen am Einheitskreis.
Trägerfunktion der rekursiven Formel für die Seitenlänge des inneren 2n-Ecks,
wenn s die Seitenlänge des n-Ecks ist.
Diese Formel ist durch geometrische Überlegungen hergeleitet.

• f:=s->sqrt(2-sqrt(4-s^2))

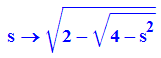
Start mit dem gleichseitigen Dreieck im Kreis

• n:=3:

Die Länge der Startseite muss man geometrisch überlegen und hier eintragen.
Beim Start mit dem Dreieck s0:=sqrt(2)

• s0:=sqrt(3); 

• (f@@k)(s) $k=1..4

• (f@@k)(s0) $k=1..4

• n*2^k $ k=1..4

• n*2^k*(f@@k)(s0) $k=1..4

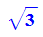
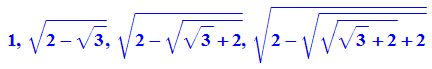
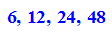
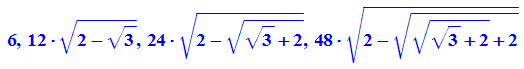
• float(n*2^k*(f@@k)(s0)) $k=1..4

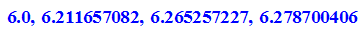
Günstig ist, nur den halben Umfang zu nehmen:

• innen:=float(n/2*2^k*(f@@k)(s0)) $k=1..8

• n*2^k $k=1..8

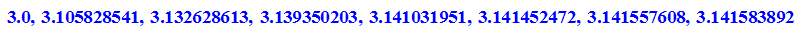
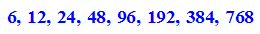
• DIGITS:=80:float(PI); DIGITS:=10:

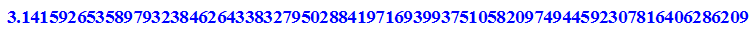
Außen-n-Ecke, rekursive Formel (Trägerfunktion).
Berechnet die Seite des umbeschriebenen 2n-Ecks aus der Seite t des n-Ecks.
Diese Formel ist "von Hand" mit geometrischen Überlegungen hergeleitet.

• g:=t->2*sqrt((sqrt(4+t^2)-2)/(sqrt(4+t^2)+2))
  

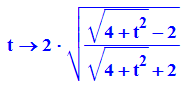
Die Länge der Startseite muss man geometrisch überlegen und hier eintragen.
Beim Start mit dem Dreieck t0:=2*sqrt(3)

• t0:=2*sqrt(3);

• (g@@k)(t) $k=1..3

• (g@@k)(t0) $k=1..3

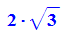
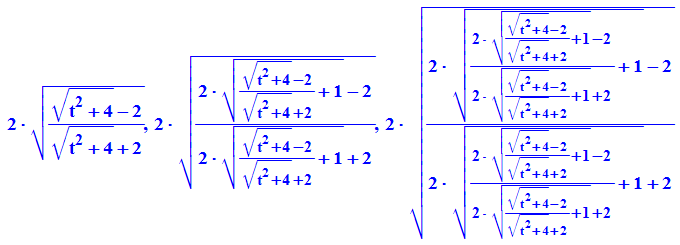
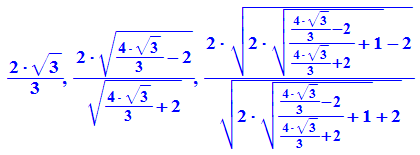
• aussen:=float(n/2*2^k*(g@@k)(t0)) $k=1..8

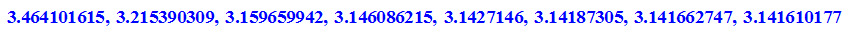
Anzeige der Fehlerspanne

• (op(aussen,k)-op(innen,k) )$k=1..8

• n*2^k $ k=1..8

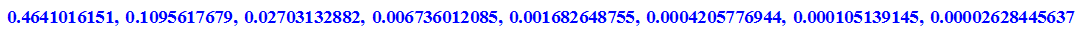
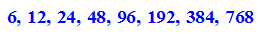
Also hat man beim beim letzen Vieleck PI zwischen

• op(innen,8);op(aussen,8)

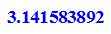
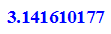
Fehler:

• float(PI)-op(innen,8);op(aussen,8)-float(PI);