Pi-Reihenformel von Ramanujan

Prof. Dr. Dörte Haftendorn, MuPAD 4,  http://haftendorn.uni-lueneburg.de  Aug.06

Automatische Übersetzung aus  MuPAD 3.11,  Jan 05

Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.

Web:  http://haftendorn.uni-lueneburg.de             www.mathematik-verstehen.de

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

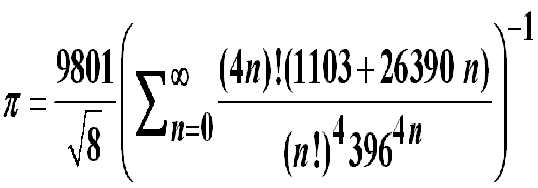
imageimageimage Seite 143...image

image

pi:=k->9801/sqrt(8)*(sum((4*n)!*(1103+26390*n)/((n!)^4*396^(4*n)),n=0..k))^(-1)

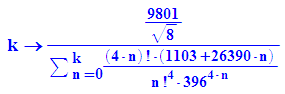
   image

 

pi(0),pi(1)

   image

 

DIGITS:=30:

liste:=pi(k) $ k=0..3;listef:=float(pi(k)) $ k=0..3

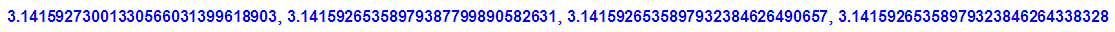
   image

   image

 

op(listef,j)-float(PI) $j=1..4;

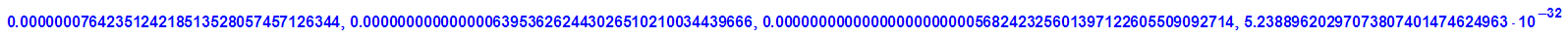
   image

 

DIGITS:=89:float(PI); float(pi(10));DIGITS:=10:

   image

   image

 

 

Hier zeigt sich, dass man schon mit einer Summation bis k=10 Pi auf 88 Stellen genau hat.