f:=(x,n)->1/n*cos(n*x)
![]()
Riemann und seine Kosinusreihen
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, JSept 07 Update 10.09.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
f:=(x,n)->1/n*cos(n*x)
![]()
plotfunc2d(f(x,n) $ n=1..10,x=-5..7, LegendVisible=FALSE)
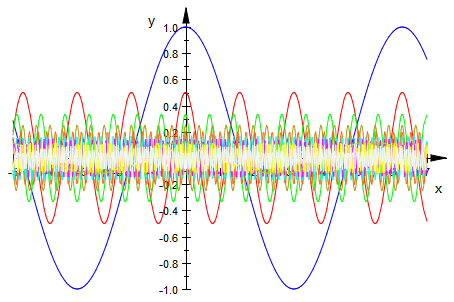
plotfunc2d(_plus(f(x,n) $ n=1..1000),x=-5..7);
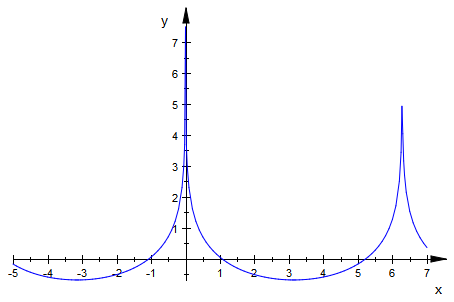
plotfunc2d(_plus(f(x,n) $ n=1..1000),x=-50..50)
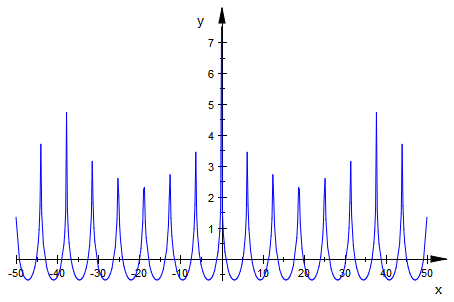
sum(1.0/n, n=1..1000)
![]()
Die Reihe divergiert sicher für ganze Vielfache von 2*PI,
da die Harmonische Reihe divergiert.
sum( f(2.0*PI,n),n=1..1000)
![]()
###########################################
Die Folgende Reihe verhält sich ganz merkwürdig:
f:=(x,n)->1/n*cos(n^2*x)
![]()
plotfunc2d(f(x,n) $ n=1..10,x=-5..15, LegendVisible=FALSE)
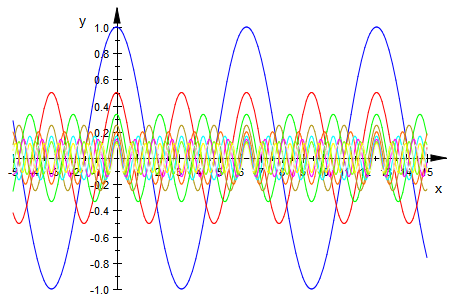
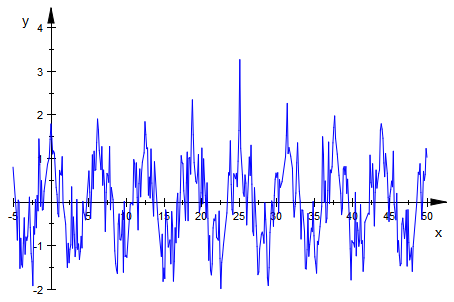
plotfunc2d(_plus(f(x,n) $ n=1..1000),x=-5..50,
ViewingBoxYRange=-2..4)
sum(1.0/n, n=1..1000),sum(f(2*PI*0.8,n), n=1..100);
![]()
sum(1.0/n, n=1..1000),sum(f(2*PI*0.8,n), n=1..1000000)
![]()
Wenn man theoretisch herangeht, zeigt sich, dass bei allen rationalen 2PI-Vielfachen die
Funktionswerte unendlich werden. D.h. die Polstellen ligen dicht. Dass man überhaupt noch etwas
sieht, liegt an der langsamen Divergenz der harmonischen Reihe.
Genaugenommen ist alles "Schrott".
sum(1.0/n, n=1..1000000),sum(f(2.0*PI,n), n=1..1000000);
![]()
sum(1/n, n=1..infinity)
![]()