f:=x->(x-1)*(x-k)*(x-5)+6
Riemann und seine Integraldefinition
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, JSept 07 Update 7.09.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
f:=x->(x-1)*(x-k)*(x-5)+6
delete k; a:=1:b:=5:
plotfunc2d(6,f,x=0..6,k=a..b, ViewingBoxYRange=-4..8)
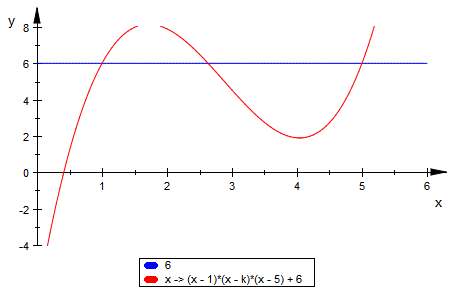
k:=3:
fg:=plot::Function2d(f(x),x=0..6,
ViewingBoxYRange=-2..10,LineWidth=0.7, LineColor=[1,0,0]):
Die Bibliothek "student::" enthält schon eine vordefinierte Möglichkeit,
Unter- und Obersummen darzustellen.
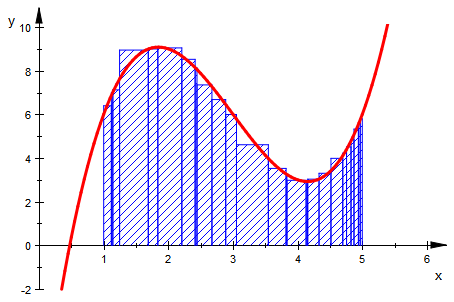
rie:=student::plotRiemann(f(x),x=a..b,10):
plot(rie,fg)
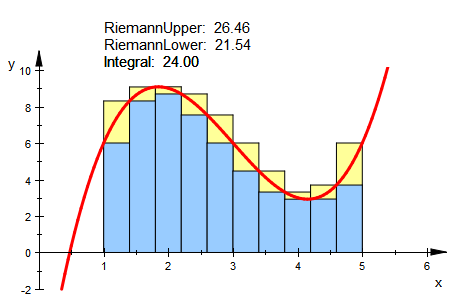
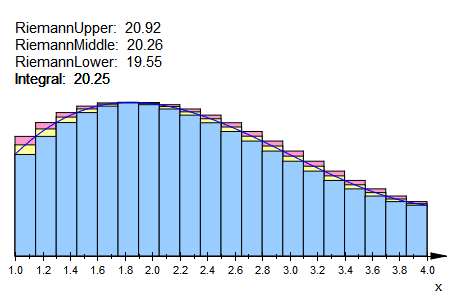
Für didaktische Zwecke kann man auch in Schritten vorgehen.
rieob:=student::plotRiemann(f(x),x=1..4,20,Lower,Middle,Upper):
plot(rieob)
Riemann hat seine Definition des Integrals in seiner Habilitationsschrift 1854
gegeben. Er brauchte eine vom Ableiten unabhängige Definition für das eigentliche
Thema: Über die Darstellbarkeit eine Funktion durch eine trigonometrische Reihe.
Es geht da um Fourierreihen zu noch nicht bekannten Funktionen. Die Kooeffizienten von Fourreihen sind
durch Integrale definiert. Er schreibt (S.239 GA) "Also zuerst: Was hat man unter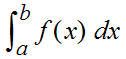 
zu verstehen?"
Es wird eine beliebige Zerlegung D des Intervalls [a,b] gewählt. Dann bildet er mit
der Ordinate je einer beliebigen Zwischenstelle jedes Teilintervalls ein Rechteck
und summiert überalle diese Rechtecke. Diese Summe heißt Riemann-Summe der Zerlegung D.
Sie liegt sicher zwischen der Obersumme und der Untersumme zu dieser Zerlegung.
Dann wird die Zerlegung verfeinert, so dass die maximale Teilintervalllänge gegen 0 geht.
Wenn dann unabhängig von der Wahl der Zerlegung und der Zwischenwerte die Riemann-Summe
einen Grenzwert hat, so heißt dieser . Anderenfalls hat das Symbol keine Bedeutung.
-----------------------------------------------------------------------------
In Folgenden wird eine Zerlegung erzeugt, indem zu einer Zufallsteilung schrittweise
ein Weiterer Punkt hinzugefügt wird.
teile:=proc(a,b)
local r,s,x;
begin
r:=frandom();
x:=a+r*(b-a);
return( [a,x,b]);
end_proc:
teile(a,b)
vereinige:=(li1,li2)->sort(listlib::removeDuplicates(li1.li2)):
Die Prozedur teile(a,b) erzeugt einen Zufallspunkt,
verfeinern(a,b,n) fügt n Zufallspunkte hinzu und gibt eine Liste der n+1
Zerlegungslisten zurück. die letzte enthält n+1 Zwischenwerte.
Daraus kann man dann n+2 Balken definieren.
verfeinern:=proc(a,b,n) /* erzeugt n+1 Zwischenwerte */
local i,alle,D1,D2;
begin
D1:=teile(a,b);
alle:=[D1];
for i from 1 to n do
D2:=vereinige(teile(a,b),D1);
alle:=alle.[D2];
D1:=D2;
end_for;
return(alle);
end_proc:
alleli:=verfeinern(a,b,4):
print(alleli[j]) $ j=1..5
[1, 4.257071429, 5]
[1, 1.458390976, 4.257071429, 5]
[1, 1.458390976, 1.990673156, 4.257071429, 5]
[1, 1.458390976, 1.990673156, 2.747420852, 4.257071429, 5]
[1, 1.458390976, 1.990673156, 2.747420852, 4.002917967, 4.257071429, 5]
alleli[3]
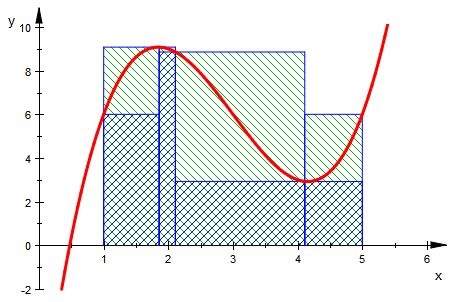
Zunächst sollen mit den erzeugten Zerlegungen Unter- und Obersummen gebildet werden.
maxi:=proc(f,a,b)
local m,mv;
begin
m:=f(a);
for i from 1 to 100 do
mv:=f(a+i/100*(b-a));
if mv>m then m:=mv end_if;
end_for;
return(float(m))
end_proc:
mini:=proc(f,a,b)
local m;
begin
m:=f(a);
for i from 1 to 100 do
mv:=f(a+i/100*(b-a));
if mv<m then m:=mv end_if;
end_for;
return(float(m))
end_proc:
Nun werden die Punkte und Rechtecke definiert.
Einzelne Schritte (unten "in einem Rutsch").
pktu:=[[li[i],mini(f,li[i],li[i+1])] $ i=1..anz-1]
polyug:=(plot::Polygon2d([[pktu[i][1],0],[pktu[i][1],pktu[i][2]],
[pktu[i+1][1],pktu[i][2]],[pktu[i+1][1],0]],
Filled=TRUE, FillColor=[0,0,1]) $ i=1..anz-2),plot::Polygon2d([[pktu[anz-1][1],0],[pktu[anz-1][1],
pktu[anz-1][2]],[li[anz],pktu[anz-1][2]],[li[anz],0]],
Filled=TRUE, FillColor=[0,0,1]);
plot(fg,polyug)
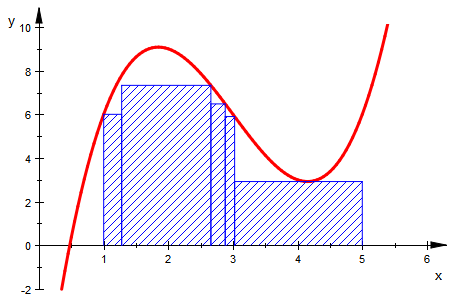
Obersummen
pkto:=[[li[i],maxi(f,li[i],li[i+1])] $ i=1..anz-1]
polyog:=(plot::Polygon2d([[pkto[i][1],0],[pkto[i][1],pkto[i][2]],
[pkto[i+1][1],pkto[i][2]],[pkto[i+1][1],0]], Filled=TRUE, FillColor=[0,0.7,0], FillPattern=FDiagonalLines) $ i=1..anz-2),plot::Polygon2d([[pkto[anz-1][1],0],[pkto[anz-1][1],
pkto[anz-1][2]],[li[anz],pkto[anz-1][2]],[li[anz],0]], Filled=TRUE, FillColor=[0,0.7,0], FillPattern=FDiagonalLines);
plot(polyog,polyug,fg)
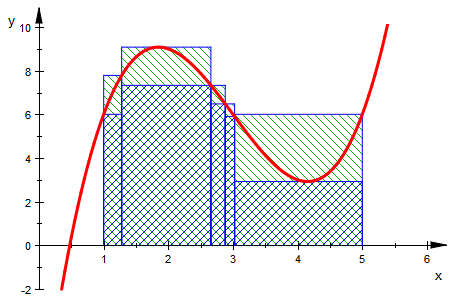
Zusammenfassung mit den Graphen aller Zerlegungen
teile(a,b) muss definiert sein. verfeinere(a,b,n) muss bekannt sein.
f, mini(f,a,b) und maxi(f,a,b), müssen bekannt sein, auch fg, der Graph von f.
Es werden die Unter-Und Obersummen-Graphiken zurückgegeben und mit f zusammen gezeichnet.
usoS:=proc(li)
local anz,pktu,pkto,polyug,polyog;
begin
anz:=nops(li);
pktu:=[[li[i],mini(f,li[i],li[i+1])] $ i=1..anz-1];
pkto:=[[li[i],maxi(f,li[i],li[i+1])] $ i=1..anz-1];
polyug:=(plot::Polygon2d([[pktu[i][1],0],[pktu[i][1],pktu[i][2]],
[pktu[i+1][1],pktu[i][2]],[pktu[i+1][1],0]],Filled=TRUE,
FillColor=[0,0,1]) $ i=1..anz-2),
plot::Polygon2d([[pktu[anz-1][1],0],[pktu[anz-1][1],
pktu[anz-1][2]], [li[anz],pktu[anz-1][2]],[li[anz],0]],
Filled=TRUE, FillColor=[0,0,1]);
polyog:=(plot::Polygon2d([[pkto[i][1],0],[pkto[i][1],pkto[i][2]],
[pkto[i+1][1],pkto[i][2]],[pkto[i+1][1],0]], Filled=TRUE,
FillColor=[0,0.7,0], FillPattern=FDiagonalLines)
$ i=1..anz-2),plot::Polygon2d([[pkto[anz-1][1],0],[pkto[anz-1][1],
pkto[anz-1][2]],[li[anz],pkto[anz-1][2]],[li[anz],0]],
Filled=TRUE, FillColor=[0,0.7,0], FillPattern=FDiagonalLines);
plot(polyog,polyug,fg);
return([polyog,polyug])
end_proc:
Bei dem folgenden Aufruf muss alleli eine Liste der Zerlegungslisten sein.
Das Feld alleg hebt alle Graphen auf.
alleg:=array(1..5):
(alleg[j]:=usoS(alleli[j])) $j=1..5 :
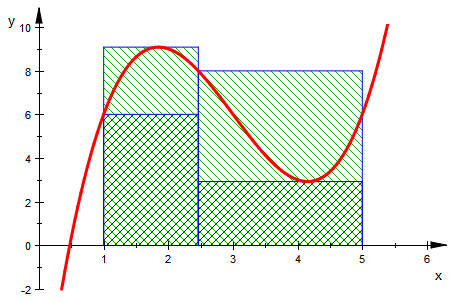
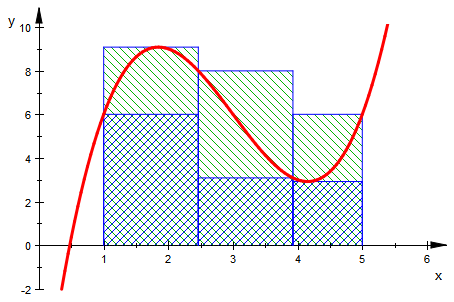
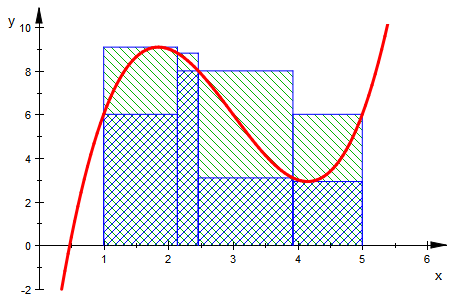
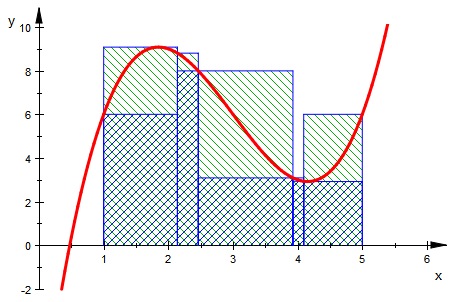
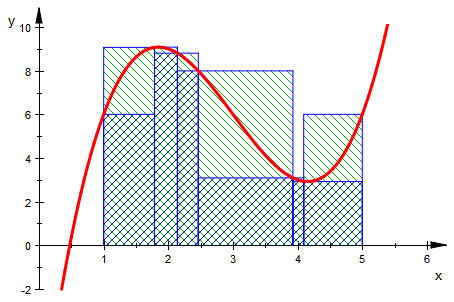
Wiederholbarer Block ################
n:=25:
alleg:=array(1..n+1): /* Tabelle der Graphen */
alleli:=verfeinern(a,b,n): /* a,b,n=Steifenzahl - 1 */
//print(alleli[j]) $ j=1..n: /* Liste aus n+1 Verfeinerungslisten */
Bei kleinem n kann man die Kommentarstriche entfernen.
Das Folgende sieht am besten aus, wenn man es auswertet.
for j from 1 to n+1 do
alleg[j]:=usoS(alleli[j]) ;
end_for:
Hier sind drei Graphiken als Bilder (da 25 Stufen zuviel Platz brauchen)
########################################
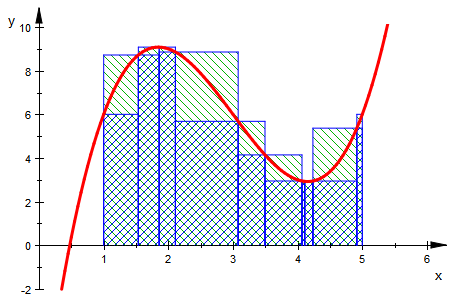
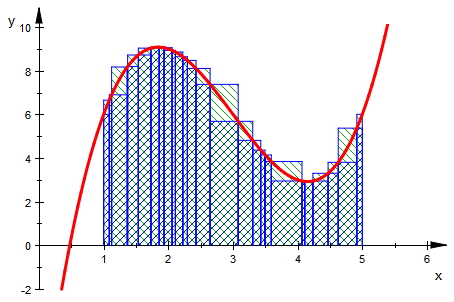
Nun wird die originale Riemann-Summe erzeugt.
Sie nimmt für die Rechtecke eine beliebige Zwischenstelle.
rieS:=proc(li)
local anz,pkt,polyg,wert,i;
begin
anz:=nops(li);
pkt:=[[li[i],f((li[i]+frandom()*(li[i+1]-li[i])))] $ i=1..anz-1];
polyg:=(plot::Polygon2d([[pkt[i][1],0],[pkt[i][1],pkt[i][2]],
[pkt[i+1][1],pkt[i][2]],[pkt[i+1][1],0]],Filled=TRUE,
FillColor=[0,0,1]) $ i=1..anz-2),
plot::Polygon2d([[pkt[anz-1][1],0],[pkt[anz-1][1],
pkt[anz-1][2]], [li[anz],pkt[anz-1][2]],[li[anz],0]],
Filled=TRUE, FillColor=[0,0,1]);
//plot(polyg,fg);
wert:=_plus((pkt[i+1][1]-pkt[i][1])*pkt[i][2] $ i=1..anz-2,(b-pkt[anz-1][1])*pkt[anz-1][2]);
return([[polyg],pkt,wert])
end_proc:
<<<<<<<< Ab hier in in einem Rutsch auswertbar.
n:=30:
allegrie:=array(1..n+2): /* Tabelle der Graphen */
allep:=array(1..n+2): /* Tabelle der Punktlisten */
allew:=array(1..n+2): /* Tabelle der Punktlisten */
alleli:=verfeinern(1,5,n): /* a,b,n=Steifenzahl - 1 */
print(alleli[j]) $ j=1..4: /* Liste aus n+1 Verfeinerungslisten */
[1, 1.092801361, 5]
[1, 1.092801361, 1.364305451, 5]
[1, 1.092801361, 1.364305451, 4.421219374, 5]
[1, 1.092801361, 1.364305451, 2.022766989, 4.421219374, 5]
Achtung, das folgende auszuwerten ist sehr eindrucksvoll. (Hier aus Platzgründen weggelassen)
for j from 1 to n+1 do
erg:=rieS(alleli[j]):
allegrie[j]:=erg[1]:
allep[j]:=erg[2]:
allew[j]:=erg[3]:
end_for:
matrix([allew[j] $ j=n-5..n+1]);//letzte Werte
Das Folgende sieht am besten aus, wenn man es auswertet.
plot(alleg[j], fg) $ j=1..n+1 ;
Wieder einige Beispiele als Bilder:
Anmerkung: Die Zerlegungen sind nicht Verfeinerungen voneinander. Das hätte man zwar einrichten können,
aber so sieht man besser, dass beim ANwenden beliebiger Zerlegungen die Konvergenz sehr langsam sein kann.
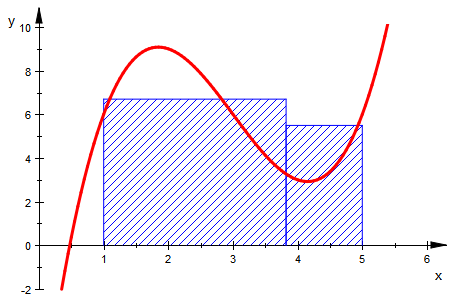
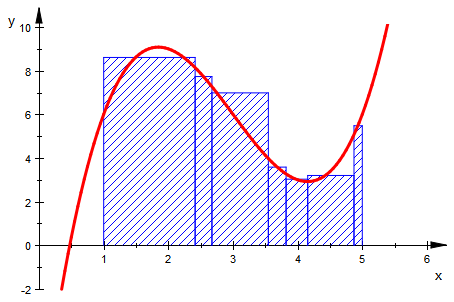
Mathematischer und didaktischer Kommentar:
Hier sind für die echten Riemann-Summen Zufallszerlegungen und zufällige Zwischenwerte genommen worden.
Das passt dazu, dass es für beliebige Zerlegungen und ZW-Werte den Grenzwert, der dann Integral heißt,
geben muss. Graphisch kann das überzeugen, allerdings ist die Konvergenz langsam.
Will man aber die Konvergenz beweisen, so ist es manchmal (zumal in der Schule) günstig, Unter- und Obersummen
zu betrachten. Haben sie für jede Zerlegung denselben Grenzwert, dann existiert das Integral sicher und ist gleich diesem Wert.
Dabei ist es naheliegend zunächst nur Intervalle mit monotonen Funktionswerten zu betrachten, da man sonst mit der Beschaffung
der maximalen und minimalen Werte in Teilintervall Mühe hat.
Bei obigem Vergehen hakt es aber auch noch: Hier ist eine zwar eine Zufallszerlegung genommen, aber eben nur eine.
Sonst nimmt man meist eine äquidistanten Zerlegung, also n gleichbreite Steifen, drückt die Unter- und Obersumme in Termen aus
und lässt dann dann n gegen unendlich laufen. Genau genommen ist das auch nur eine Zerlegung mit ihrer Verfeinerungsreihe.
Bei den in der Schule und der Grundausbildung relevanten Funktionen (den stetigen und beschränkten) ist das aber dennoch
vollständig, da man das Einschließungskriterium anwenden kann.
Daher ist auch nichts dagegen einzuwenden, wenn MuPAD unter dem Stichwort "Riemannsches Integral"
"Unter- und Obersummen bei gleichbreiten Steifen" betrachtet.
Entscheidend ist, dass die Riemannsche Definition des Integrals völlig unabhängig vom Ab- und Aufleiten ist.
Für stetige Funktionen stellt der Hauptsatz der Differential- und Integralrechung diesen Zusammenhang erst her.
Riemann selbst gibt ein Beispiel einer in gar keinem noch so kleinen Intervall stetigen Funktion, die dennoch
mit seiner Definition integrierbar ist. Sie Extradatei rieman-unstet-int.mn.