B(i*1/10) $ i=0..20
![]()
Riemanns in keinem Intervall integrierbare Funktion
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Sept 07 Update 5.09.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Dateiname riemann-unstet-int.mn
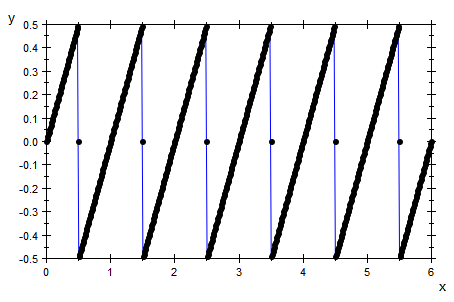
Dieser Bestandteil B der Riemann-Funktion sorgt für die Unstetigkeitsstellen.
B:=x->if abs(2*x-round(2*x))<10^(-10)
then 0 else x-round(x) end_if;
x -> (if abs(2*x - round(2*x)) < 10^(-10) then
0
else
x - round(x)
end_if)
B(i*1/10) $ i=0..20
![]()
B(i*0.1) $ i=0..20
![]()
b1g:=plot::Listplot([[i/100,B(i/100)] $ i=0..600] ):
plot(b1g)
Riemanns NI-Funktion ist die unendliche Summe der B-Terme: .
f:=(x,n)->sum(B(i*x)/i,i=1..n)
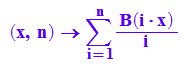
Veranschaulichung der Bausteine :
n:=11:
bg:=array(1..n):
bg[1]:=plot::Listplot([[i/100,B(i/500)] $ i=0..500], PointsVisible=FALSE, LineColor=[0,0,1] ):
bg[2]:=plot::Listplot([[i/100,B(2*i/500)/2] $ i=0..500],PointsVisible=FALSE, LineColor=[1,0,0] ):
bg[3]:=plot::Listplot([[i/100,B(3*i/500)/3] $ i=0..500],PointsVisible=FALSE, LineColor=[0,1,0] ):
bg[4]:=plot::Listplot([[i/100,B(4*i/500)/4] $ i=0..500],PointsVisible=FALSE, LineColor=[1,0,1] ):
bg[5]:=plot::Listplot([[i/100,B(5*i/500)/5] $ i=0..500],PointsVisible=FALSE, LineColor=[1,0.5,0] ):
bg[6]:=plot::Listplot([[i/100,B(6*i/500)/6] $ i=0..500],PointsVisible=FALSE, LineColor=[0,0,0] ):
bg[7]:=plot::Listplot([[i/100,B(7*i/500)/7] $ i=0..500],PointsVisible=FALSE, LineColor=[1,1,0] ):
bg[8]:=plot::Listplot([[i/100,B(8*i/500)/8] $ i=0..500],PointsVisible=FALSE, LineColor=[0,0,1] ):
bg[9]:=plot::Listplot([[i/100,B(9*i/500)/9] $ i=0..500],PointsVisible=FALSE, LineColor=[0,0.8,0] ):
bg[10]:=plot::Listplot([[i/100,B(10*i/500)/10] $ i=0..500],PointsVisible=FALSE, LineColor=[1,1,0] ):
bg[11]:=plot::Listplot([[i/100,B(11*i/500)/11] $ i=0..500],PointsVisible=FALSE, LineColor=[0.5,0,1] ):
plot(bg[i] $ i=1..n-3)
Die Steigungen sind 1. Die Sprungstellen liegen bei den
ungeraden Vielfachen von 1/(2n).
Die Sprunghöhen sind 1/n
Aufgrund des Umweges über Einzelpunkte sind die bei den Sprungstellen die Senkrechten mitgezeichnet.
---------------------------------------------------------------------
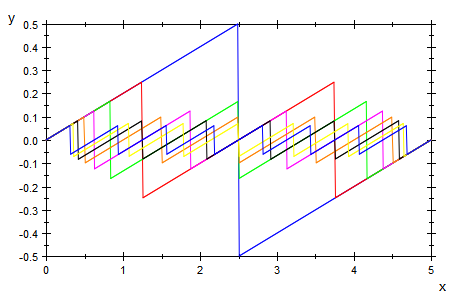
Nun werden alle diese Funktionen addiert.
Aus technischen Gründen wird das Intervall in 6000 Teile geteilt.
fplatz ist also die diskrete Version von f.
Hier werden konkret nur 11 Funktionen, f(x,1) bis f(x,11) addiert.
nenner:=6000:
fplatz:=i->B(1*i/nenner)/1+B(2*i/nenner)/2+B(3*i/nenner)/3+B(4*i/nenner)/4+ B(5*i/nenner)/5+B(6*i/nenner)/6+B(7*i/nenner)/7+B(8*i/nenner)/8+B(9*i/nenner)/9+
B(10*i/nenner)/10+B(11*i/nenner)/11
![]()
fplatz(0.3) //Probe, es werden auch Zwischenwerte berechnet.
![]()
fganz:=plot::Listplot([[i/nenner,fplatz(i)] $ i=0..nenner],
PointsVisible=FALSE, LineColor=[1,0,0] ):
xachse:=plot::Function2d(0,x=0..1,LineColor=[0,0,0]):
plot(fganz,xachse)
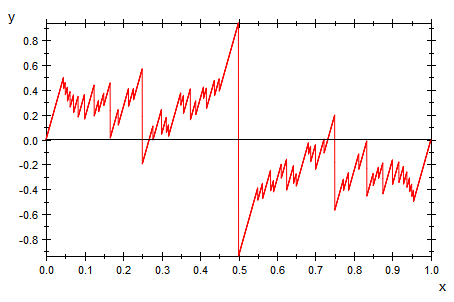
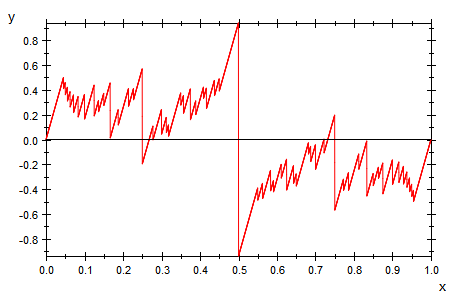
Das ist der Graph der Riemann-Funktion.
Mit noch mehr Punkten als 6000 erreicht man kein anderes Bild.
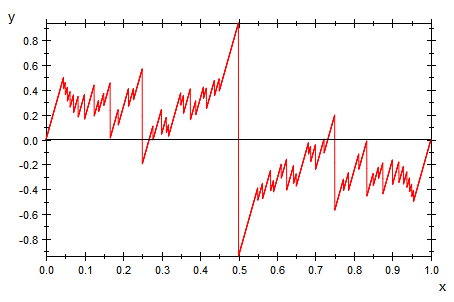
Riemanns Funktion ist in keinem Intervall stetig.
Die Unstetigkeitsstellen liegen dicht.
Sie ist nicht integrierbar.
Erzeugen der Verfeinerung: (Verfeinerung, .... unter "Datei, Eigenschaften" eingetragen.
Es sind die in der Datei riemann-int entwickelten Prozeduren.)
alleli:=verfeinern(0,1,4):
print(alleli[j]) $ j=1..5
[0, 0.2703567032, 1]
[0, 0.2703567032, 0.8142678572, 1]
[0, 0.1145977439, 0.2703567032, 0.8142678572, 1]
[0, 0.1145977439, 0.247668289, 0.2703567032, 0.8142678572, 1]
[0, 0.1145977439, 0.247668289, 0.2703567032, 0.436855213, 0.8142678572, 1]
Selbstverständlich würde es jetzt nicht leicht fallen, in jedem Intervall
Maximum und Minimum zu finden. Daher nimmt Riemann den Funktionswert
an einer beliebigen Zwischenstelle in jedem Intervall.
rieS:=proc(li)
local anz,pkt,polyg,wert;
begin
anz:=nops(li);
pkt:=[[li[i],fplatz((li[i]+frandom()*(li[i+1]-li[i]))*nenner)] $ i=1..anz-1];
polyg:=(plot::Polygon2d([[pkt[i][1],0],[pkt[i][1],pkt[i][2]],
[pkt[i+1][1],pkt[i][2]],[pkt[i+1][1],0]],Filled=TRUE,
FillColor=[0,0,1]) $ i=1..anz-2),
plot::Polygon2d([[pkt[anz-1][1],0],[pkt[anz-1][1],
pkt[anz-1][2]], [li[anz],pkt[anz-1][2]],[li[anz],0]],
Filled=TRUE, FillColor=[0,0,1]);
//plot(xachse,polyg,fganz);
wert:=_plus((pkt[i+1][1]-pkt[i][1])*pkt[i][2] $ i=1..anz-2)+(1-pkt[anz-1][1])*pkt[anz-1][2];
return([[polyg],pkt,wert])
end_proc:
Wiederholbarer Block ################
n:=50:
alleg:=array(1..n+2): /* Tabelle der Graphen */
allep:=array(1..n+2): /* Tabelle der Punktlisten */
allew:=array(1..n+2): /* Tabelle der Punktlisten */
alleli:=verfeinern(0,1,n+1): /* a,b,n=Steifenzahl - 1 */
//print(alleli[j]) $ j=1..n+1: /* Folge aus n+1 Verfeinerungslisten */
Für die Zahlenwerte die Auskommentierung entfernen.
Das folgende in der MuPad-Datei auswerten. Das sieht am Eindrucksvollsten aus.
for j from 1 to n+1 do
erg:=rieS(alleli[j]):
alleg[j]:=erg[1]:
allep[j]:=erg[2]:
allew[j]:=erg[3]:
end_for:
matrix([allew[j] $ j=n-5..n+1]);
allep[j] $ j=1..3:
plot(xachse,alleg[j*10], fganz)$ j=1..5 ;
Das sind drei Teilungen und die Riemannschen Summen (als Bilder).
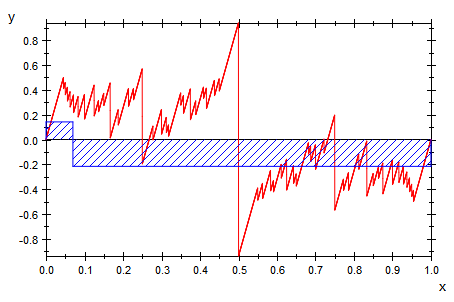
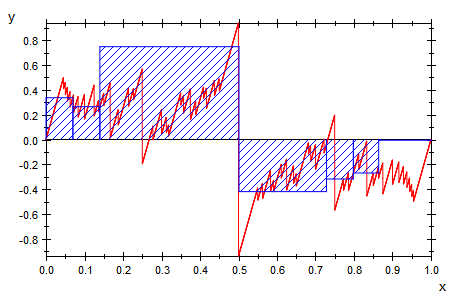
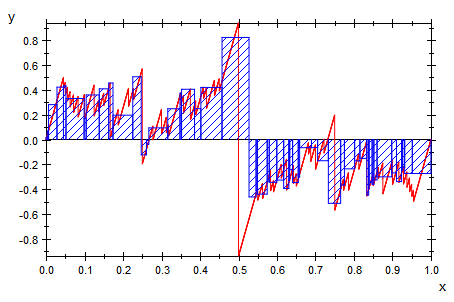
Das sind Bilder der Riemannschen Summen,
weil mit der Geamtauswertung die Datei zu groß wird.
---------------------------------------------
Theoretische Untersuchung der auftretenden Summen
sum(1.0/((2*i-1)),i=1..10000000000000)
![]()
sum(1/(2*i-1),i=1..infinity)
![]()
Die Sprunghöhen werden unendlich
und nicht mehr endlich
float(sum(1.0/((2*i-1))/n,i=1..11)) $ n=1..5
![]()
Die Sprunghöhen passen nicht sonderlich gut zu der Zeichnung.
Und zwar sind sie alle zu klein. Das wiederum ist klar
float(sum(1.0/((2*i-1))/n,i=1..5)) $ n=1..5
![]()
Es summieren sich ja nicht alle 11 auf eine Stelle bei nur 50 Werten.
die mit 5 Werten passt schon besser.
Die ersten Sprünge sind bei den geraden Stammbrüchen
1/2,1/4,1/6,1/8,1/10
![]()