Graphentheorie 1

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn April 2011

0.1 Handling

0.2 Inhalt

1 Graphen erzeugen und zeichnen,
          dort wichtige Funktionen abschicken!
1.1 Spielwiese zum Ausprobieren
1.2 Einige Zufallsgraphen zum Lernen
1.3 Reparatur bei der Adjazenzmatix
1.4 Anzeige der Adjazenzmatix und Graphenerzeugung aus ihr.
2 Erzeugung eigener Graphen mit Gewichtung
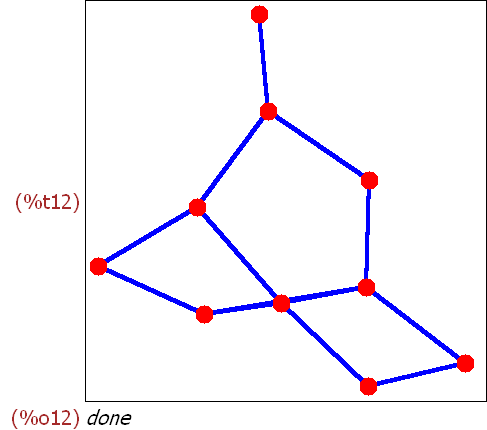
2.1 Kleiner gewichteter Graph
2.2 Spannbaum und kürzester Weg im Lüneburg-Graphen (mein Buch S.64)
2.3 Spannbaum und kürzester Weg im Dijkstra-Graphen (mein Buch S.65)
2.4 Weitere Graphen und Spannbäume
3 Bipartite und vollständige Graphen
3.1 Erzeugung bipartiter Graphen und Zeichnung
3.2 Vollständige Graphen
4 Graphen mit besonderen Namen

1 Graphen erzeugen und zeichnen

(%i3) load(graphs)$
load(draw)$

Diese beiden Bibliotheken muss man unbedingt zu Beginn laden. (doppelt abschicken!)
In der Hilfe findet man mit dem Suchwort graphs das Kapitel 53.
Dort stehen alle Funktionen zum Erzeugen, Zeichnen und Untersuchen von Graphen.
Hier treffe ich eine Auswahl, die zu meinem Lehrplan (Fachwissenschaft, Gym-Lehramt) passt.

--> my:random_graph(5,0.3);

Hier wird ein Zufallsgraph mit 5 ecken erzeugt, bei dem zufällig
30% der möglichen Kanten gesetzt werden

--> draw_graph(my,vertex_size=3,show_edges=edges(my),show_edge_width=4);

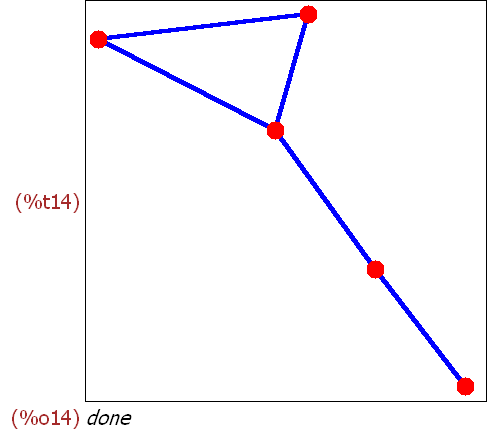
Im Zeichenbefehl sind gleich noch einige Eigenschaften gesetzt.

Reparaturfunktion abschicken !!!

(%i5) adjazenz_matrix(g):=block(local(A,BB,i,j,li),
             A:adjacency_matrix(g),
             li:matrix_size(A),
             array(BB,fixnum,li[1],li[2]),
             for i:1 thru li[2] do
                 for j:1 thru li[1] do
                     BB[i,j]:A[li[1]-i+1,li[2]-j+1],
                  endfor,
              endfor,
   genmatrix(BB,li[1],li[2])
)$

1.1 Spielwiese zum Ausprobieren

--> sp:my:random_graph(5,0.6)$
draw_graph(sp,vertex_size=3,show_id=true,
                       show_edges=edges(my),show_edge_width=4)$

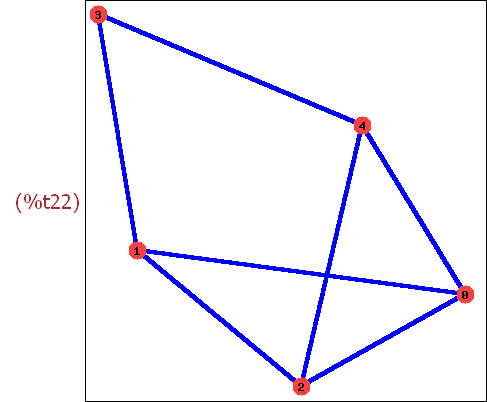
1.2 Einige Graphen zum Lernen

Achtung, bei erneuter Auswertung würden diese Graphen sich verändern!

--> my:random_graph(10,0.3)

--> draw_graph(my,vertex_size=3,show_edges=edges(my),show_edge_width=4);

--> my:random_graph(10,0.4);

--> draw_graph(my,vertex_size=3,show_id=true,
show_edges=edges(my),show_edge_width=4);

--> my:random_graph(10,0.2);

--> draw_graph(my,vertex_size=3,show_id=true,
show_edges=edges(my),show_edge_width=4);

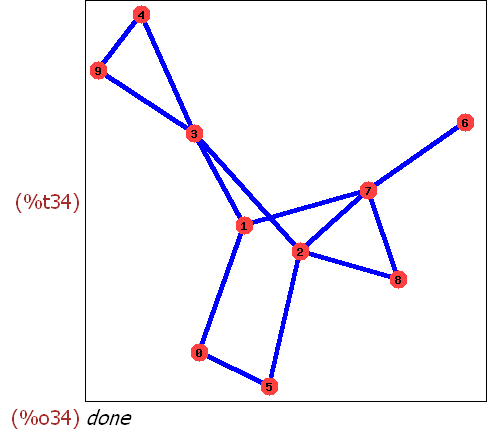
--> my:random_graph(10,0.3);

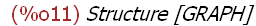
--> draw_graph(my);

Von dem nachfolgenden Eintrag aus der Hilfe habe ich die Optionen abgeguckt.

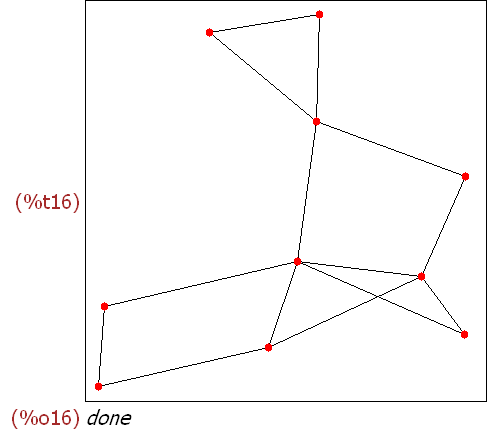
--> g:create_graph(16,
    [
     [0,1],[1,3],[2,3],[0,2],[3,4],[2,4],
     [5,6],[6,4],[4,7],[6,7],[7,8],[7,10],[7,11],
 [8,10],[11,10],[8,9],[11,12],[9,15],[12,13],
     [10,14],[15,14],[13,14]
    ])$
 t:minimum_spanning_tree(g)$
draw_graph(g,
    show_edges=edges(t), show_edge_width=4,
    show_edge_color=green,
    vertex_type=filled_square, vertex_size=2
    )$

--> my:random_graph(10,0.4);

--> draw_graph(my,vertex_size=3,show_id=true,
show_edges=edges(my),show_edge_width=4);

1.3 Reparatur der Anzeige der Adjazenzmatrix und
Erzeugen mit einer Adjazenzmatix

1.4 Anzeige der Adjazenzmatrix und
Erzeugen mit einer Adjazenzmatix

Aufstellen einer Matrix

--> A:matrix( [0,1,0,1,1],[1,0,1,1,1],[0,1,0,1,0] ,[1,1,1,0,0] ,[1,1,0,1,0] );

--> amy:from_adjacency_matrix (A)$
draw_graph(amy,show_id=true, edge_color=green, edge_width=3);

--> print_graph(amy);adjazenz_matrix(amy);

2 Erzeugung eigener Graphen mit Gewichtung

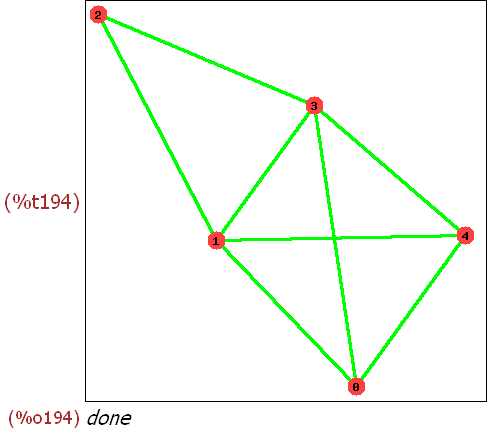
2.1 Kleiner gewichteter Graph

--> g : create_graph([0,1,2,3],[[[0,1], 1], [[1,2], 2], [[2,3], 3],
                          [[3,0], 4],[[0,2], 5]])$
draw_graph(g,show_id=true, edge_color=green,
                edge_width=2,show_weight=true);
print_graph(g)$

--> A:adjazenz_matrix(g); AA:adjacency_matrix(g);

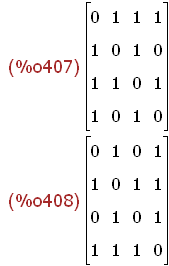
Die reparierte Adjazenzmatix ist richtig,
die vom Originalbefehl ausgegebene Adjazenzmatrix ist rückwärts sortiert.
Sie würde beim Konstruieren nicht auf den ursprünglichen Graphen führen.

2.2 Spannbaum und kürzeste Wege im Lüneburg-Graphen, S.

(%i36) eckenglg:[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]$

(%i37) kantenglg:[[[1,2],2],[[1,3],3],[[2,3],3],[[3,4],1],[[4,5],4],[[3,6],1],[[4,7],3],[[5,8],2],[[6,7],2],[[7,8],1],
[[8,9],2],[[9,10],3],[[10,11],3],[[11,12],1],[[7,13],4],[[8,15],4],[[9,16],5],[[10,16],4],[[13,14],4],[[15,14],2],[[15,16],1]]$

(%i38) glg:create_graph(eckenglg,kantenglg)$

(%i39) draw_graph(glg,show_id=true,show_weight=true,edge_color=green,edge_width=3);

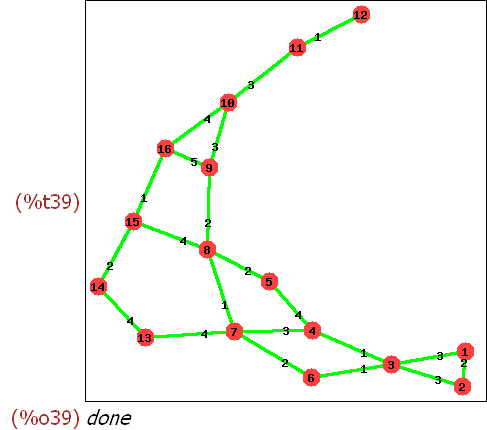
(%i40) t : minimum_spanning_tree(glg);print_graph(t);

(%i42) draw_graph(glg,show_id=true,show_weight=true,edge_color=green,edge_width=3
            ,show_edges=edges(t),show_edge_color=purple,show_edge_width=5
        );

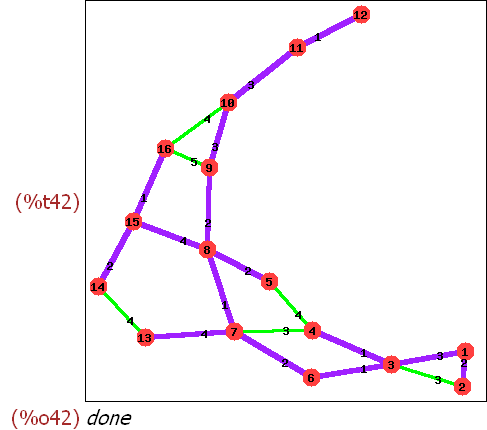
(%i43) for i:1 thru 16 do print(shortest_weighted_path(14, i, glg)),endfor;

(%i44) weglg:[[2,3],[3,6],[6,7],[7,8],[8,15],[15,14]]$

(%i45) draw_graph(glg,show_id=true,show_weight=true,edge_color=green,edge_width=3
            ,show_edges=weglg,show_edge_color=purple,show_edge_width=5
        );

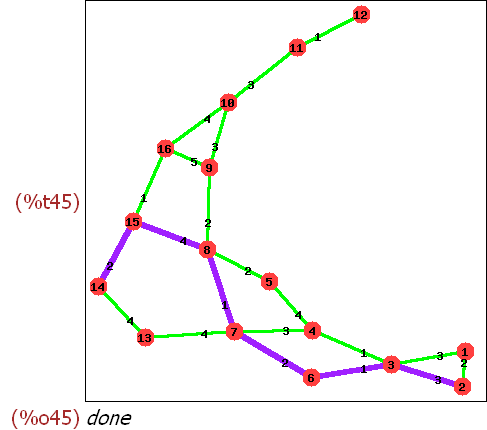
2.3 Der Spannbaum und Dijkstra-Graph aus meinem Buch, S. 65

(%i46) ecken:[[1,"A"],[2,"B"],[3,"C"],[4,"D"],[5,"E"],[6,"F"],[7,"G"],[8,"H"],[9,"I"]];

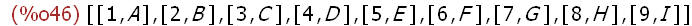
(%i47) kanten:[[[1,2],1],[[1,5],9],[[1,4],2],[[2,3],6],[[2,5],7],[[3,6],2],[[3,7],6],
              [[4,5],5],[[4,8],3],[[5,6],5],[[5,9],2],[[5,8],1],[[6,7],1],[[6,9],2],[[7,9],4],[[8,9],4]]$

(%i48) gb:create_graph(ecken,kanten)$

(%i49) draw_graph(gb,show_label=true,show_weight=true,edge_color=green,edge_width=3);

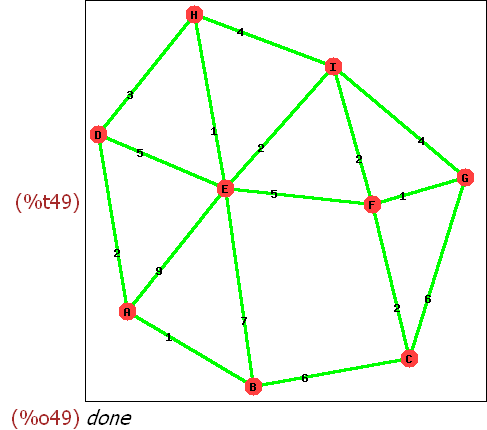
Leider bekomme ich die Schrift nicht größer hin.

Spannbaum

(%i50) t : minimum_spanning_tree(gb);print_graph(t);

(%i52) draw_graph(gb,show_label=true,show_weight=true,edge_color=green,edge_width=3
        ,show_edges=edges(t),show_edge_color=purple,show_edge_width=5 );

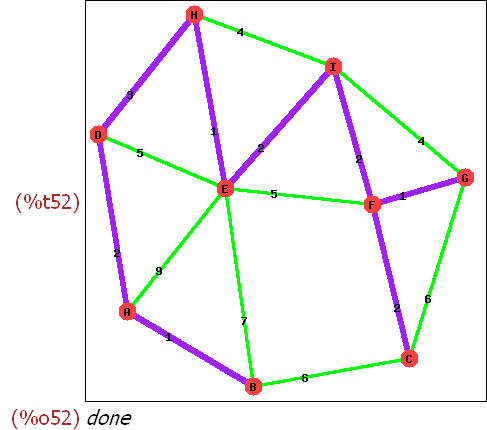
So ist es auch auf Seite 65 gefunden.

Kürzeste Wege direkt von Maxima:

--> for i:1 thru 9 do print(shortest_weighted_path(1, i, gb)),endfor;

--> weg:shortest_weighted_path(1, 9, gb);

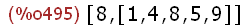
Von Hand habe ich daraus Kantenzüge gemacht.

--> dijweg:[[1,4], [4,8],[8,5],[5,9]];dijweg2:[[1,2],[2,3],[3,6],[6,7]];

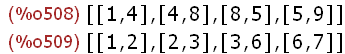
Man kann einen Teilgraphen anders Färben aber leider nicht zwei Teilgraphen.

--> draw_graph(gb,show_label=true,show_weight=true,edge_color=green,edge_width=3,
       show_edges=dijweg,show_edge_color=yellow,show_edge_width=5
      /* ,show_edges=dijweg2,show_edge_color=purple,show_edge_width=5*/
        );

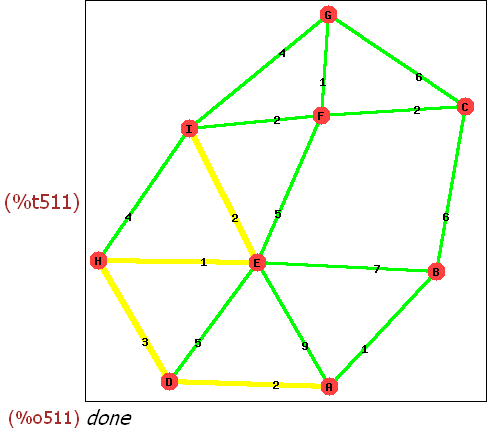
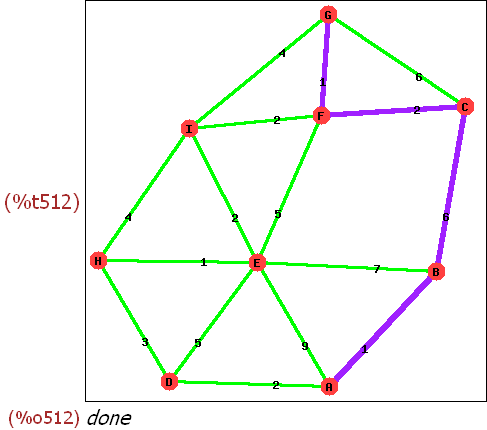
--> draw_graph(gb,show_label=true,show_weight=true,edge_color=green,edge_width=3
      /*, show_edges=dijweg,show_edge_color=yellow,show_edge_width=5 */
       ,show_edges=dijweg2,show_edge_color=purple,show_edge_width=5
        );

2.4 Weitere Graphen und Spannbäume

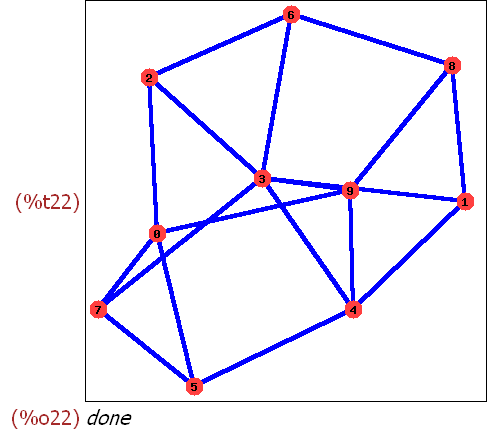
(%i59) gsp:random_graph(10,0.3)$

(%i61) draw_graph(gsp,show_id=true,edge_color=green,edge_width=3);

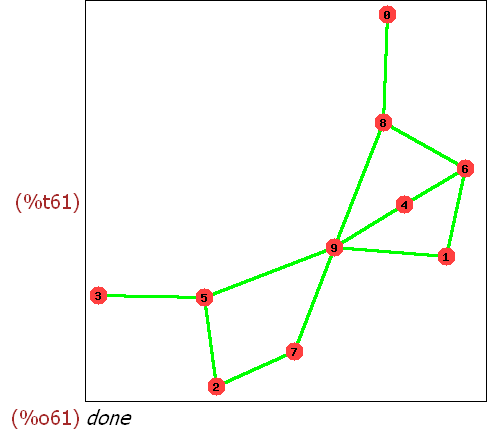
Spannbaum

(%i64) t : minimum_spanning_tree(gsp);print_graph(t);

(%i66) draw_graph(gsp,show_id=true,show_weight=true,edge_color=green,edge_width=3
        ,show_edges=edges(t),show_edge_color=purple,show_edge_width=5 );

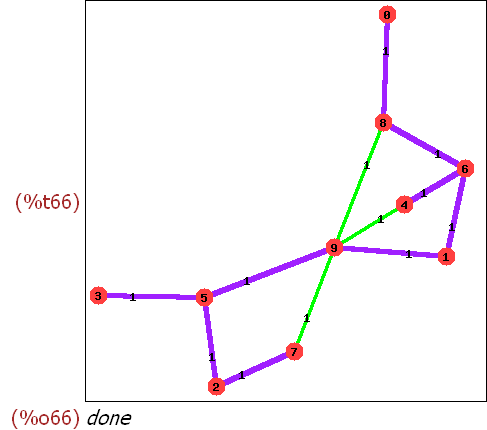
Wenn ich mir das ansehe, glaube ich eher, dass "Tiefensuche" programmiert ist.

3 Bipartite und vollständige Graphen

3.1 Erzeugung

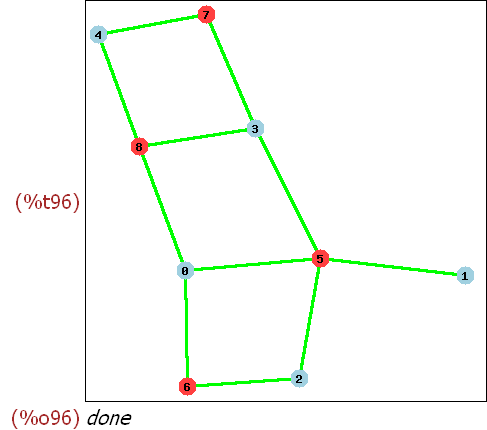
(%i93) big:random_bipartite_graph (5, 4, 0.8);

(%i94) [A,B]:bipartition(big);

(%i95) print_graph(big);

(%i96) draw_graph(big,show_id=true,edge_color=green,edge_width=3,show_vertices=A);

(%i97) draw_graph(big,show_id=true,edge_color=green,edge_width=3);

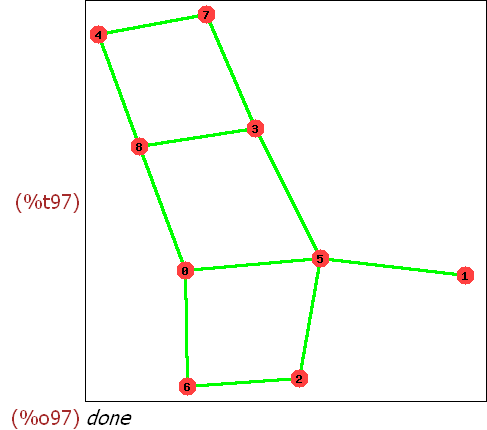
Noch einmal

(%i98) big:random_bipartite_graph (5, 4, 0.8);

(%i102) draw_graph(big,show_id=true,edge_color=green,edge_width=3);

(%i99) [A,B]:bipartition(big);

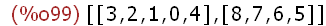
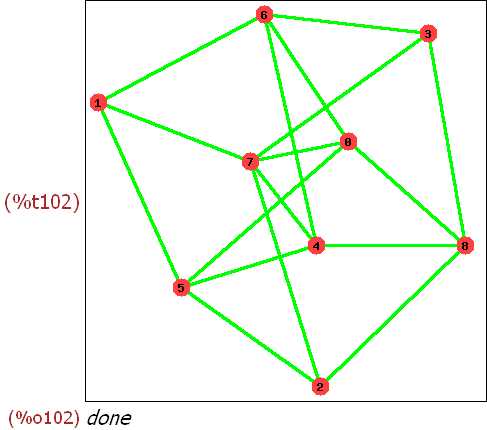
(%i103) print_graph(big);

(%i104) draw_graph(big,show_id=true,edge_color=green,edge_width=3,show_vertices=A);

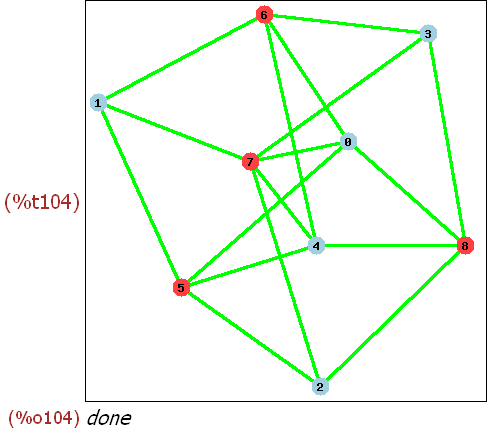
Wenn ich mir das so ansehe, ist [0,3,4] zu [8,7,6] ein vollständiger
bipartiter Teilgraph. Damit ist der Graph nicht planar.

(%i105) is_planar(big);

War ja klar.

3.2 Vollständige Graphen

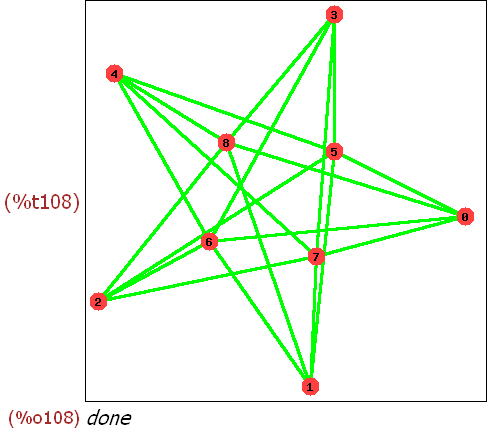
(%i106) bipvo:complete_bipartite_graph (5, 4);

(%i108) draw_graph(bipvo,show_id=true,edge_color=green,edge_width=3);

(%i109) [A,B]:bipartition(bipvo);

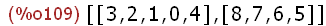
(%i110) print_graph(bipvo);

(%i111) draw_graph(bipvo,show_id=true,edge_color=green,edge_width=3,show_vertices=A);

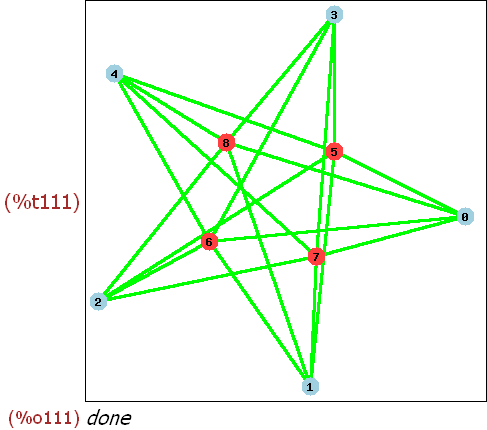
(%i116) vo:complete_graph (7);
draw_graph(vo,show_id=true,edge_color=green,edge_width=3);

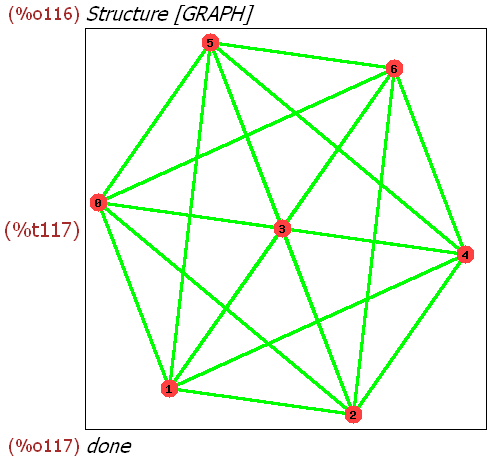
4 Graphen mit besonderen Namen

Noch nicht ausgeführt. In der Hilfe steht etliches.