
Knotentheorie Alexanderpolynome
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Nov. 07 Update 2.11.07
www.mathematik-verstehen.de http://haftendorn.uni-lueneburg.de
#######################################################################


alm:=matrix(6,6):
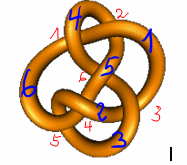
Trage ein oben, weggehend, ankommend bei Linkskreuzung
Trage ein oben, ankommend, weggehend bei Rechtskreuzung
Jede Zeile bezieht sich auf eine Kreuzung.
alm[1,4]:=1-t:alm[1,1]:=t:alm[1,6]:=-1:
alm[2,1]:=1-t:alm[2,5]:=t:alm[2,4]:=-1:
alm[3,3]:=1-t:alm[3,1]:=t:alm[3,2]:=-1:
alm[4,2]:=1-t:alm[4,5]:=t:alm[4,6]:=-1:
alm[5,6]:=1-t:alm[5,2]:=t:alm[5,3]:=-1:
alm[6,5]:=1-t:alm[6,4]:=t:alm[6,3]:=-1:
alm

Das ist die Alexander-Matrix.
Aus ihr streicht man eine Zeile und eine Spalte
almex:=matrix(5,5):
Hier wird die letzte Zeile und letzte Spalte gestrichen.
for i from 1 to 5 do
for j from 1 to 5 do
almex[i,j]:=alm[i,j]
end_for
end_for:
Dadurch entsteht die reduzierte Alexandermatrix
almex

Ihre Determinante ist das Alexanderpolynom
linalg::det(almex)
![]()
################################