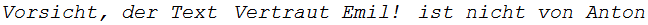El-Gamal-Verfahren und DSS-Signatur

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Jan 2011+Dez 12

0.1 Handlinghilfen

Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.
Dazu Shift halten, dann werden auch alle Unterebenen aufgeklappt.

Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.

Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf (mit sh klick),
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

0.2 Inhalt

Figure 1:

1 Schüsselerzeugung

Anton, Berta und Tobi wollen gemeinsam kommunizieren. Dazu müssen
sie sich auf eine Verschlüsselungsfunktion einigen, und zu zwei
Zahlen p und g ein gemeinsame öffentliche Schlüsselliste erstellen.

1.1 Verabredung von p und g

p wird als Primzahl gewählt.

(%i2) p:next_prime(floor(sqrt(random(1.0)*10^122)));
10^60;

(%i4) g:random(p-2);
10^60;

Als kleines Beispiel eignet sich p:113; g:97

1.2 Verschlüsselungsfunktion

Es muss irgendeine invertierbare Funktion gewählt werden.
Sie soll die Nachricht und den jeweiligen Kommunikationsschlüssel
miteinander verrechnen.
Der Einfachheit haber wird hier das gewöhnliche Produkt genommen.

(%i6) f(k,m):=k*m; f_inv(k,c):=c/k;

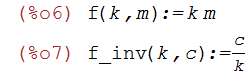
1.3 Öffentliche Schlüsselliste

Die drei wählen jeder für sich geheime Zahlen ta,tb,tt und
bilden den öffentlichen Teil Ihres Schlüssels

Anton

(%i8) ta:random(p-2);
tAnton:power_mod(g,ta,p);

Berta

(%i10) tb:random(p-2);
tBerta:power_mod(g,tb,p);

Tobi

(%i12) tt:random(p-2);
tTobi:power_mod(g,tt,p);

Die Öffentliche Schlüsselliste ist nun

(%i14) tAnton; tBerta; tTobi;

2 Hilfsfunktionen

(%i17) txToZoo(text):=block([i,li,intli,n,z],
                      li:charlist(text),n:length(li), intli:[],
                      for i:1 thru n do (
                         intli:append(intli,[cint(li[i])]) ), print(intli),
       intli:intli-28, print(intli),z:0,
                       for i:1 thru n do (z:z*100+intli[i]), return(z)
                      )$

(%i18) txToZoo("Affe");

(%i19) zooToTx(z):=block([i,li,zz,tx],
                    intli:[],zz:z,tx:"",
                    for i:1 while zz>=1 do(
                       intli:append([mod(zz,100)],intli), zz:floor(zz/100)),
                    print(intli), intli:intli+28, print(intli),
                    for i:1 thru length(intli) do (tx:concat(tx,ascii(intli[i]))),
                    return(tx)
                    )$

(%i20) m:zooToTx(37747473);

3 Sendung

Jeder der drei kann sich nun entschließen, den beiden anderen
etwas zu senden. Hier will Anton an Berta und Tobi eine geheime
Nachricht senden.

3.1 Vorbereitung

Anton wählt geheim ein a und bildet eine Zahl antonOffen,
der er zusammen mit der verschlüsselten Nachricht verschicken wird.

(%i21) a:random(p-2);
antonOffen:power_mod(g,a,p);

Er berechnet für die Kommunikation mit Berta einen Schlüssel k_AB.
Er berechnet für die Kommunikation mit Tobi einen Schlüssel k_AT.

(%i23) k_AB:power_mod(tBerta,a,p);
k_AT:power_mod(tTobi,a,p);

3.2 Verwendung der Nachricht

(%i36) m:txToZoo("Erster Montag 2012 um Zehn");

(%i37) A_an_Berta:f(k_AB,m);
A_an_Tobi:f(k_AT,m);

Achtung, Berta und Tobi erhalten für dieselbe Nachricht verschiedene
Kryptogramme.

3.3 Sendung

Berta erhält

(%i39) antonOffen;
A_an_Berta;

Tobi erhält

(%i41) antonOffen;
A_an_Tobi;

3.4 Empfang und Entschlüsselung

Berta stellt sich auch ihren Kommnuikationsschlüssel kb_AB
für Nachrichen von Anton her. Es ist derslbe Schlüssel wie k_AB.

(%i43) kb_AB:power_mod(antonOffen,tb,p);
is(kb_AB=k_AB);

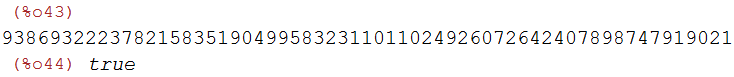
Berta rechnet

--> B_von_Anton:f_inv(kb_AB,A_an_Berta);
klarB:zooToTx(B_von_Anton);

Tobi stellt sich auch seinen Kommnuikationsschlüssel kc_AT
für Nachrichen von Anton her. Es ist derslbe Schlüssel wie k_AT.

(%i45) kt_AT:power_mod(antonOffen,tt,p);
is(kt_AT=k_AT);

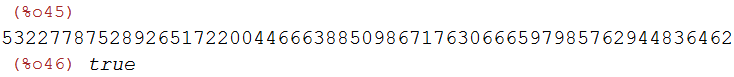
Tobi rechnet

(%i47) T_von_Anton:f_inv(kt_AT,A_an_Tobi);
klarT:zooToTx(T_von_Anton);

4 Signatur mit ElGamal= DSS

DSS= digital Signatur Standard, Anton will eine Nachricht
signieren, Berta und Tobi sollen sie verifizieren können

4.1 Offene Nachricht und Vorbereitung

(%i49) klar:"Vertraut Emil nicht!";

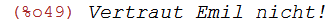
(%i50) m:txToZoo(klar);

Anton wählt eine Zahl ra teilerfremd zu p-1 und
bestimmt ihre Inverse ri bezüglich p-1.

(%i51) p;

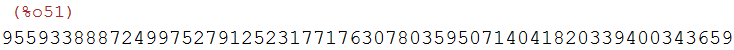
(%i52) ra:2$ while gcd(ra,p-1)#1 do ra:random(p-1)$ ra;

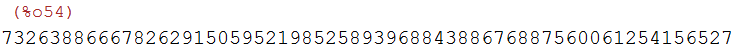
(%i55) gcd(ra,p-1);

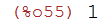
(%i60) ri:gcdex(ra,p-1)[1]$ if ri<0 then ri:ri+p-1$ ri;

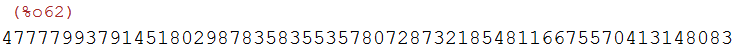
Probe

(%i63) mod(ra*ri,p-1);

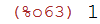
(%i64) kra:power_mod(g,ra,p);

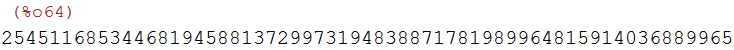
4.2 Erzeugung der Signatur

(%i65) sa:mod((m-ta*kra)*ri,p-1);

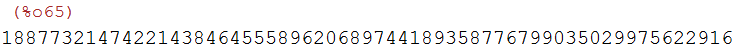
Anton sendet nun

--> [klar,m,sa,kra];

4.3 Prüfung der digitalen Unterschrift

Jeder, der p,g und tAnton kennt, kann prüfen, ob dies
wirklich Antons Text ist.
Er berechnet zwei Zahlen und prüft, ob die gleich sind.

(%i72) test1:power_mod(g,m,p);
test2:mod(power_mod(tAnton,kra,p)*power_mod(kra,sa,p),p);

(%i74) if test1=test2 then print("Anton hat wirklich geschrieben: ",klar)
   else print("Vorsicht, der Text ",zooToTx(m), " ist nicht von Anton")$

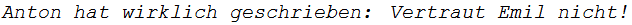
4.4 Veränderung von m

(%i75) klarx:"Vertraut Emil!"$
m:txToZoo(klarx);

(%i77) test1:power_mod(g,m,p);
test2:mod(power_mod(tAnton,kra,p)*power_mod(kra,sa,p),p);

(%i79) if test1=test2 then print("Anton hat wirklich geschrieben: ",klar)
   else print("Vorsicht, der Text ",klarx, " ist nicht von Anton")$