Fiat-Shamir-Verfahren

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Jan 2011

0.1 Handlinghilfen

0.2 Inhalt

Figure 1:

1 Schüsselerzeugung

Anton will Berta davon überzeugen, dass er ein Geheimnis kennt,
ohne dass Berta irgendetwas von dem Geheimnis erfährt.

1.1 Erzeugung von n aus p und g

p und q werden als Primzahlen gewählt.

(%i10) p:next_prime(floor(sqrt(random(1.0)*10^122)));
q:next_prime(floor(sqrt(random(1.0)*10^122)));
10^60;

n wird als Produkt gebildet:

(%i13) n:p*q;

1.2 Geheimnis und öffentliche Schlüssel

(%i14) s:random(n-2);
10^120;

(%i16) v:power_mod(s,2,n);

Als kleines Beispiel eignet sich p:11; q:17; s:137
Öffentlich ist v und n:

(%i17) v; n;

2 Anwendungsphase

2.1 Antons Tat

Anton wählt r teilerfremd zu n und berechnet x und sendet x.

(%i19) n;

(%i20) r:random(n-2)$
while gcd(r,n)#1 do r:random(n-2)$
x:power_mod(r,2,n);

2.2 Bertas Tat

Berta empfängt x und sendet b=0 oder b=1

(%i23) makelist(random(2),i,1,200);

(%i24) b:random(2);

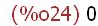
2.3 Anton empfängt und antwortet

Anton empfängt b und sendet y: bei b=0 das y=r, bei b=1 das y=rs modn

(%i25) if b=0 then y:r else y:mod(r*s,n);

2.4 Berta empfängt y und testet

(%i26) test:power_mod(y,2,n);

(%i27) b;

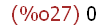
(%i28) if b=0 then (if test=x then erg:"ok" else erg:"Quaaark")
     else (if test=mod(x*v,n) then erg:"ok so" else erg:"Quark")$
erg;

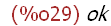
3 Mehrere Durchläufe

3.1 Automatischer Einmaltest

(%i77) teste():=block([r,x,b,y,test,erg],r:random(n-2),
              while gcd(r,n)#1 do r:random(n-2), x:power_mod(r,2,n),
              b:random(2), if b=0 then y:r else y:mod(r*s,n),
              test:power_mod(y,2,n),
              if b=0 then (if test=x then erg:"ok" else erg:"Quaaark")
                 else (if test=mod(x*v,n) then erg:"JA" else erg:"Quark"),
              return(erg) )$

(%i170) [teste(),teste(),teste(),teste(),teste(),teste(),teste(),teste()];

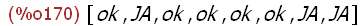
3.2 Automatisch viele Tests

(%i79) z:10$ sp:15$

Definition von Arrays
Achtung: offenbar kann man Array nicht so eingach neu belegen.
Darum wird hier mit kill() das Array gelöscht,
damit ein echt neuer Durchlauf kommt.

(%i125) kill(t)$ t[i,j]:=teste();
tm:genmatrix(t,z,sp);

Alle Einträge mit JA bzw. ok behalten ihre Koordinaten,
die jeweils anderen werden rechts abgelegt.

(%i128) kill(tmJA)$ tmJA[i,j]:=if tm[i,j]="JA" then [i,j] else [z+1,1];
kill(tmok)$ tmok[i,j]:=if tm[i,j]="ok" then [i,j] else [z+1,2];

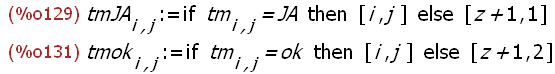
(%i133) tmJA[2,1];

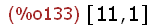
(%i38) load(draw)$

(%i184) liJA:[]$ for j from 1 thru sp do liJA:append(liJA,makelist(tmJA[i,j],i,1,z))$ liJA$
liok:[]$ for j from 1 thru sp do liok:append(liok,makelist(tmok[i,j],i,1,z))$ liok$

Es war etwas mühsam, die Punkte passend aufzubereiten.
Eine Matrix aus Punkten wurde nicht akzeptiert.
Nun ist eine Liste aus Punkten jeweils erzeugt.

(%i142) pkt:gr2d(color=red, point_size=2,point_type=5, points(liJA),
              color=green, point_size=2,point_type=7, points(liok))$
draw(pkt)$

Figure 2:

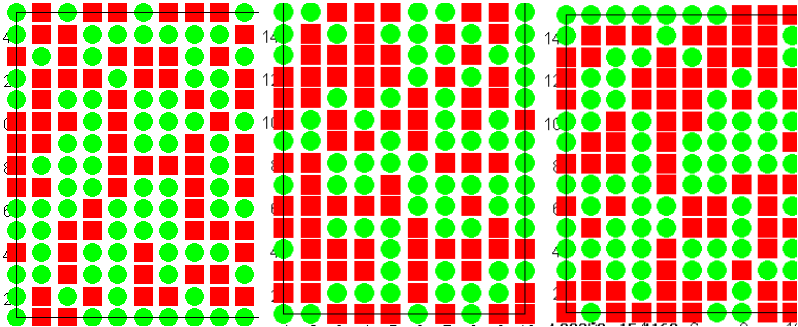
Dies sind also drei Serien aus 150 Durchläufen.
Die Wahrscheinlichkeit, dass Mister X so oft richtig rät ist:

(%i190) 1/2^150,numer;

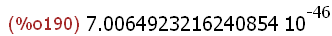
also etwa so groß, wie im Weltall ein bestimmtes Atom
zufällig genau zu treffen.