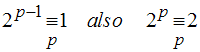.Ist 2^n mod 2 = 2 ein Primzahl-Test?
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02,(ex. in 3.11 Sept. 05) Feb.07
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
####################################################################
Wenn p prim, dann ist .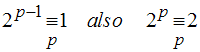
Kleiner Fermatscher Satz
Gilt das auch umgekehrt?
Antwortversuch in Einfach-Programmierung,
Suche auch in anderen Bereichen. Erwickle eine bessere Prozedur.
test:=n->if powermod(2,n,n)=2 then factor(n)else "" end_if;
n -> (if powermod(2, n, n) = 2 then
factor(n)
else
""
end_if)
test(n)$ n=1..1000;
test(n)$ n=1000..2000;
11*31; 2^% mod %
3*11*17; 2^% mod %
3*5*43; 2^% mod %
3*13*17; 2^% mod %
19*73; 2^% mod %
7*13*19; 2^% mod %
3*5*127; 2^% mod %
Also sind bis 2000 mind. 7 Ausnahmen gefunden worden.
Wenn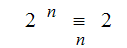 
,dann folgt nicht unbedingt, dass n prim ist.
Dies ist also kein Primzahltest.
Es lohnt sich aber weitere Prüfungen erst anzustellen,
wenn 2^n mod n =2 ist.
Diese Bedingung ist notwendig aber nicht hinreichend.