ggt-prg4

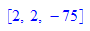
ggtex erweiterter Euklidischer Algoritmus mit Textausgabe

Programmierung mit MuPAD Die Prozeduren sind dann in dem package zahltheo verborgen.

Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02, (ursprünglich 02 ex. in 3.11 Sept. 05) Feb.07

http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de

####################################################################

Aufruf: ggtex(a,b)

ggtex:=proc(a,b)

local r0,r1,r2,q0,s0,s1,s2,t0,t1,t2;

begin

r0:=a: r1:=b: q0:=a div b: s0:=1: s1:=0: t0:=0: t1:=1:

repeat

r2:=r0 mod r1:

if r2=0 then

print(Unquoted,"ggT(".a.",".b.")= ".r1.

" VSD ".r1."= ".s1."*".a."+ (".t1.")*".b);

return([r1,s1,t1]);

end_if;

q0:= r0 div r1: s2:=s0-q0*s1: t2:=t0-q0*t1:

print(Unquoted,

" ".r0."=".q0."*".r1."+".r2." und es ist VSD ".r2."= ".s2."*".a."+ (".t2.")*".b);

r0:=r1: r1:=r2: s0:=s1: t0:=t1: s1:=s2: t1:=t2:

/*alle eine Nummer herunterzählen */

until 3=5 end_repeat;

end_proc:

gg:=ggtex(676,18)

676=37*18+10 und es ist VSD 10= 1*676+ (-37)*18

18=1*10+8 und es ist VSD 8= -1*676+ (38)*18

10=1*8+2 und es ist VSD 2= 2*676+ (-75)*18

ggT(676,18)= 2 VSD 2= 2*676+ (-75)*18

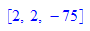
Herausgreifen der wichtigen Zahlen

gg[1],gg[2],gg[3]

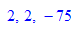
Untensteht eine Extra-Funktion für ggT.

Ablaufverfolgung um die Prozedur zu entwickeln und zu testen.

delete a,b,r0,r1,r2,q0,q1,s0,s1,s2,t0,t1,t2;

[r0,r1,r2,q0,s0,s1,s2,t0,t1,t2] ;

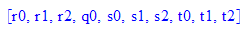
a:=676:b:=18:

r0:=a: r1:=b: q0:=a div b: s0:=1: s1:=0: t0:=0: t1:=1:

[r0,r1,r2,q0,s0,s1,s2,t0,t1,t2];

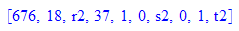
---------Marke 1--------------- ab hier wiederholt auswerten --------------------------------------------

r2:=r0 mod r1:

if r2=0 then

print(Unquoted,"ggT(".a.",".b.")= ".r1.

" VSD ".r1."= ".s1."*".a."+ (".t1.")*".b);

return([r1,s1,t1]);

end_if;

ggT(676,18)= 2 VSD 2= 2*676+ (-75)*18

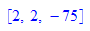
Aufhören, wenn hier der hier der ggT erscheint.

q0:= r0 div r1: s2:=s0-q0*s1: t2:=t0-q0*t1:

print(Unquoted,

" ".r0."=".q0."*".r1."+".r2." und es ist VSD ".r2."= ".s2."*".a."+ (".t2.")*".b);

10=1*8+2 und es ist VSD 2= 2*676+ (-75)*18

[r0,r1,r2,q0,s0,s1,s2,t0,t1,t2];

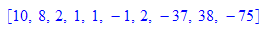
r0:=r1: r1:=r2: s0:=s1: t0:=t1: s1:=s2: t1:=t2:

[r0,r1,r2,q0,s0,s1,s2,t0,t1,t2];

/*alle eine Nummer herunterzählen */

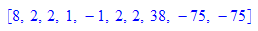
-------gehe zu Marke 1 ab hier zurück ---------------------------------------------------

Variante ohne die Textausgabe

ggte:=proc(a: Type::Integer,b:Type::Integer)

local r0,r1,r2,q0,q1,s0,s1,s2,t0,t1,t2;

begin

r0:=a: r1:=b: q0:=a div b: s0:=1: s1:=0: t0:=0: t1:=1:

repeat

r2:=r0 mod r1:

if r2=0 then

return([r1,s1,t1]);

end_if;

q0:= r0 div r1: s2:=s0-q0*s1: t2:=t0-q0*t1:

r0:=r1: r1:=r2: s0:=s1: t0:=t1: s1:=s2: t1:=t2:

/*alle eine Nummer herunterzählen */

until 3=5 end_repeat;

end_proc:

ggte(676,18)

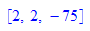
Variante nur ggt

ggt:=proc(a: Type::Integer,b:Type::Integer)

local r0,r1,r2,q0,q1;

begin

r0:=a: r1:=b:

repeat

r2:=r0 mod r1:

if r2=0 then return(r1)

end_if;

q0:= r0 div r1:

q1:= r1 div r2:

r0:=r1: r1:=r2: q0:=q1:

/*alle eine Nummer herunterzählen */

until r2=0 end_repeat;

end_proc:

ggt(676,115)

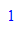
WeitereTests, Vergeich mit eingebauten Funktionen

a:=676: b:= 37: ggt(a,b), gcd(a,b),ggte(a,b), igcdex(a,b);

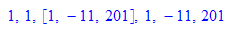
ggtex(a,b)

676=18*37+10 und es ist VSD 10= 1*676+ (-18)*37

37=3*10+7 und es ist VSD 7= -3*676+ (55)*37

10=1*7+3 und es ist VSD 3= 4*676+ (-73)*37

7=2*3+1 und es ist VSD 1= -11*676+ (201)*37

ggT(676,37)= 1 VSD 1= -11*676+ (201)*37

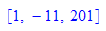
a:=666: b:= 37: ggt(a,b), gcd(a,b),ggte(a,b), igcdex(a,b),ggtex(a,b);

ggT(666,37)= 37 VSD 37= 0*666+ (1)*37

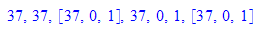
Also der größte gemeinsame Teiler ist von MuPAD direkt zu erreichen mit

gcd(a,b) greates common divisor

Der erweiterte Euklidische Algorithmus wird von

igcdex(a,b) integer gcd extended ausgeführt. Ausgegeben wird eine Folge

a:=676:b:=37: ig:=igcdex(a,b)

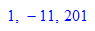
Probe

-11*676+201*37

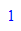
ig[1]=ig[2]*a+ig[3]*b // Automatisch

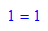
gg:=ggtex(a,b)

676=18*37+10 und es ist VSD 10= 1*676+ (-18)*37

37=3*10+7 und es ist VSD 7= -3*676+ (55)*37

10=1*7+3 und es ist VSD 3= 4*676+ (-73)*37

7=2*3+1 und es ist VSD 1= -11*676+ (201)*37

ggT(676,37)= 1 VSD 1= -11*676+ (201)*37

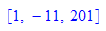
gg[1]=gg[2]*a+gg[3]*b // Automatisch