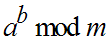
Powermod: Programmierung von pmod(a,b,m)
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02, (ex. in 3.11 Sept. 05) Feb.07
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
####################################################################
Der wichtigste Term der Kryptographie ist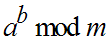
Dabei sind alle drei Variablen riesige Zahlen mit einer Dezimalen Stellenlänge weit über 100.
Aber auch schon im bescheidenen Rahmen einer Berechung mit 3-stelligen Zahlen in der Lehre
kann man (ohne großes CAS) nicht einfach die Potenz ausrechnen und dann den modularen Rest bestimmen:
pot:=109^47
pot mod 211
Alle großen CAS haben dafür den Befehl powermod(a,b,m) (in irgeneiner Syntax), bei dem
mit geschickten Zwischenrechnungen immer sofort modular "heruntergebrochen" wird.
Kleinen CAS, insbesondere CAS-Taschenrechnern wie dem TI-voyage, fehlt diese Fkt.
Die unten entwickelte Prozedur kann -unter Beachtung kleiner Sytaxanpassungen- sofort
auf den TI-voyage (oder TI92 ) übertragen werden. download der TI-Datei ist möglich.
Grundidee Es werden nacheinander "Potenztürme" gebaut:
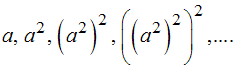Bei der Entscheidung, ob ein solcher Turm als Faktor zum
Aufbau von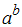 
benötigt wird hilft die Dualdarstellung des Exponenten b.
Zum Beispiel b=11. Dann ist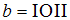 
und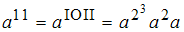 
.
Nun braucht man aber diese Dualdarstellung nicht explizit zu erzeugen, sondern man
nutzt die "Doublel-Daddel-Methode" statt zum Erzeugen der Dualzahl gleich zu Erzeugen der Potenz.
"Doublel-Daddel-Methode" zum Erzeugen der Dualzahl ---->Extraseite
Programmierung von pmod(a,k,m) #######################
pmod:=proc(a: Type::Rational,k: Type::Integer,m: Type::Integer)
local x,kk,pot;
begin
kk:=k; x:=1: pot:=a:
if k<0 then kk:=-k: pot:=1/a: end_if;
//Abfangen negativer Exponenten
if k=0 then
if a<>0 then return(1);
elif a=0 then return ("unbestimmt");
end_if;
end_if;
//Abfangen von a^0 und 0^0
repeat
if kk mod 2 =1 then
x:= x*pot mod m ;
if kk=1 then return(x); end_if;
kk:=kk-1; //hiernach ist k gerade
end_if;
kk:= kk/2; //immer möglich
pot:= pot*pot mod m;
until 3=5 end_repeat;
end_proc:
pmod(27,5,31);
powermod(27,5,31); // MuPAD-Funktion
Die folgende Matrix zeigt, dass das eigene pmod und das eingebaute powermod
für einige positive Eingaben identische Werte liefern.
matrix([[[pmod(a,k,31),powermod(a,k,31)] $ k=25..31]
$ a=27..30]);
Übrigens kann man an dieser Liste schon sehen, dass bei Potenzen im Modul
allerlei Besonderheiten auftauchen, die man erkunden kann.
Siehe Extraseite zu Potenzen.
Tests zu Sonderfällen ##############################
powermod(2,0,7);
pmod(2,0,7);
powermod(0,0,7);
pmod(0,0,7);
Na, da ist das eigene pmod sogar besser!
Als Basis können rationale Zahlen genommen werden,
denn der mod-Befehl von MuPAD kann diese verarbeiten.
pmod(15/13,1,17)
15/13 mod 17
Probe
i13:=(1/13 mod 17);
i13*13 mod 17;
(15*i13)*13 mod 17;
Auch negative Basen können genommen werden.
-3 mod 11;
pmod(-3,5,11);
powermod(-3,5,11);
Beide Funktionen verarbeiten auch negative Exponenten,
powermod(2,-3,11);
pmod(2,-3,11);
7*2^3 mod 11 //Probe
