ggtex(342,99)
342=3*99+45 und es ist VSD 45= 1*342+ (-3)*99
99=2*45+9 und es ist VSD 9= -2*342+ (7)*99
ggT(342,99)= 9 VSD 9= -2*342+ (7)*99
![]()
Definition eigener Prozeduren im Package zahltheo
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02, (in3.11 Sept. 05) Feb.07
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
####################################################################
verwendet auch im TI92/Voyage
Es ist gut möglich, die Prozeduren hier in MuPAD zu entwickeln und auszutesten und
sie dann erst für der TI umzuschreiben.
1. ggtex(a,b) erweiterter Euklidischer Algorithmus mit vollständiger Textausgabe
Rückgabe [ggt,s,t]
2. ggte(a,b) erweiterter Euklidischer Algorithmus ohne Textausgabe
Rückgabe [ggt,s,t]
3. ggt(a,b) Euklidischer Algorithmus Rückgabe zahl
4. teiler(a) Liste der Teiler von a
5. zstern(n) die Liste der zu n Teilerfremden, also Zm*
5a. ordo(a,m) Ordnung des Elementes a in Zm*
Zusatz: Potenztafeln
____________________________________________________
6. Umwandlungen Extraseite
7. powermod Extraseite
*************************************************************************************************************
// zahltheo- Package
// Zahlenteoretische Ergänzungen
// Dörte Haftendorn September 05 und Feb. 07
//#######################################
// ggtex(a,b) erweiterter Euklidischer Algorithmus mit vollständiger Textausgabe
ggtex:=
proc(a: Type::Integer,b:Type::Integer)
local r0,r1,r2,q0,s0,s1,s2,t0,t1,t2;
begin
r0:=a: r1:=b: q0:=a div b: s0:=1: s1:=0: t0:=0: t1:=1:
repeat
r2:=r0 mod r1:
if r2=0 then
print(Unquoted,"ggT(".a.",".b.")= ".r1.
" VSD ".r1."= ".s1."*".a."+ (".t1.")*".b);
return([r1,s1,t1]);
end_if;
q0:= r0 div r1: s2:=s0-q0*s1: t2:=t0-q0*t1:
print(Unquoted,
" ".r0."=".q0."*".r1."+".r2." und es ist VSD ".r2."= ".s2."*".a."+ (".t2.")*".b);
r0:=r1: r1:=r2: s0:=s1: t0:=t1: s1:=s2: t1:=t2:
/*alle eine Nummer herunterzählen */
until 3=5 end_repeat;
end_proc:
ggtex(342,99)
342=3*99+45 und es ist VSD 45= 1*342+ (-3)*99
99=2*45+9 und es ist VSD 9= -2*342+ (7)*99
ggT(342,99)= 9 VSD 9= -2*342+ (7)*99
![]()
ggtex(297,99)
ggT(297,99)= 99 VSD 99= 0*297+ (1)*99
![]()
Nun als Funktion oder Textausgabe
ggte:=
proc(a: Type::Integer,b:Type::Integer)
local r0,r1,r2,q0,s0,s1,s2,t0,t1,t2;
begin
r0:=a: r1:=b: q0:=a div b: s0:=1: s1:=0: t0:=0: t1:=1:
repeat
r2:=r0 mod r1:
if r2=0 then
return([r1,s1,t1]);
end_if;
q0:= r0 div r1: s2:=s0-q0*s1: t2:=t0-q0*t1:
r0:=r1: r1:=r2: s0:=s1: t0:=t1: s1:=s2: t1:=t2:
/*alle eine Nummer herunterzählen */
until 3=5 end_repeat;
end_proc:
ggte(65,26)
![]()
***************************************************************************************************
//zahltheo- Package
// Zahlenteoretische Ergänzungen
// Dörte Haftendorn September 05
//#######################################
//ggt(a,b) Euklidischer Algorithmus
ggt:=
proc(a: Type::Integer,b:Type::Integer)
local r0,r1,r2,q0,q1;
begin
r0:=a: r1:=b:
repeat
r2:=r0 mod r1:
if r2=0 then return(r1)
end_if;
q0:= r0 div r1:
q1:= r1 div r2:
r0:=r1: r1:=r2: q0:=q1:
/*alle eine Nummer herunterzählen */
until r2=0 end_repeat;
end_proc:
ggt(56,36 )
![]()
################################################################
//zahltheo- Package
// Zahlenteoretische Ergänzungen
// Dörte Haftendorn September 05
//#######################################
// teiler(a)
teiler:=proc(a)
local i,t;
begin
t:=[]:
for i from 1 to floor(sqrt(a)) do
if modp(a,i)=0 then
t:=append(t,i,a/i)
end_if:
end_for:
return(t):
end_proc:
teiler(100)
![]()
Man kann hier die Teilerpaare sehen.
******************************************************************************************************
################################################################
//zahltheo- Package
// Zahlenteoretische Ergänzungen
// Dörte Haftendorn September 05
//#######################################
// zstern(n) die Liste der zu n Teilerfremden
zstern:=proc(n: Type::Integer)
local i,liste;
begin
liste:=[]:
for i from 1 to n do
if gcd(n,i)=1 then liste:=liste.[i]
end_if:
end_for:
return (liste);
end_proc:
zstern(27)
![]()
ordo:=proc(a: Type::Integer,m: Type::Integer)
local ordnung, pot;
begin
ordnung:=1: pot:=modp(a,m):
if gcd(a,m)>1 then return("".a." nicht teilerfremd zu ".m); end_if;
while pot>1 do
pot:=modp(pot*a,m): ordnung:=ordnung+1
end_while;
if pot=1 then return( ordnung); end_if;
end_proc:
ordo(5,17)
![]()
5^k mod 17 $ k=1..16
![]()
ordo(9,17)
![]()
9^k mod 17 $ k=1..16
![]()
Entdecken kann man die Ordnung an den Potenztafeln
potenzTafelListe:=proc(liste,m,n)
local i,k;
begin
print(liste, " Potenzen modulo ".m);
matrix([i $ i=1..n]),
matrix([[k^i mod m $ k in liste] $ i=1..n]);
end_proc:
potenzTafelListe([3,7,9],10,8)
[3, 7, 9], " Potenzen modulo 10"
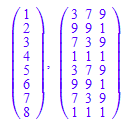
Man kann die zstern direkt einsetzen:
m:=15:
potenzTafelListe(zstern(m),m,nops(zstern(m)))
[1, 2, 4, 7, 8, 11, 13, 14], " Potenzen modulo 15"

##########################################################################
Umwandlungen auf Extraseite
1. textToZahl (w) Umwandlung mit Ascii direkt
2. zahlToText(w) Umwandlung mit Ascii direkt
3. txToZoo(w) Umwandlung Text in Zahl, je Buchstabe 2 Ziffern
4. zooToTx(z) Umwandlung Zahl in Text, je Buchstabe 2 Ziffern
5. caesar(k,w) Cäsarverschlüsselung Verschiebung um k
6. raseac(k,wz) Inverse dazu
Powermod auf Extraseite