54 mod 7 //infix-Schreibweise
![]()
Restklassenstrukturen
Prof. Dr. Dörte Haftendorn, Mathematik mit MuPAD 4.02,
(ex. in 2.5 vom Nov.02 und in 3.11 Sept. 05) Feb.07
http://haftendorn.uni-lueneburg.de www.mathematik-verstehen.de
####################################################################
Diese Datei verwendet kein PACKAGE
Berechnen der Reste
54 mod 7 //infix-Schreibweise
![]()
modp(54,7), _mod(54,7) // präfix-Schreibweisen
![]()
Diese Arten arbeiten mit positiven Resten von 0 bis m-1.
Dagegen verwendet mods bei der Ausgabe negative Reste.
mods(i,7) $ i=0..6 // verwendet negative Reste
![]()
Negative Zahlen bei der Eingabe werden richtig behandelt:
[-33 mod 7 ,modp(-33,7), mods(-33,7)]
![]()
Stammbrüche bei der Eingabe geben die richtigen Inversen an:
[1/3 mod 7 ,modp(1/3,7), mods(1/3,7)]
![]()
Beliebige Brüche bei der Eingabe werden richtig behandelt:
[11/3 mod 7 ,modp(11/3,7), mods(11/3,7)];
[11*(5 mod 7) mod 7, modp(11/3,7)*modp(3/11,7) mod 7 ];
![]()
![]()
Plustafeln und Maltafeln der Restklassen-Struktur ###############
Sie werden hier als Funktionen des Moduls definiert.
m:=7:
plustafel:=m->array(1..m,1..m, [[i+j mod m $ i=0..m-1 ] $ j=0..m-1]):
maltafel:=m->array(1..m-1,1..m-1, [[i*j mod m $ i=1..m-1 ] $ j=1..m-1]):
plustafel(m),maltafel(m);

plustafel(6), maltafel(6)

plustafel(5), maltafel(5)

Rechnen mit Restklassen.
a:=76:b:=40:m:=7:
print(a,b,a+b,a mod m, b mod m);
print("((a mod m)+ (b mod m)) mod m) =?= ((a+b) mod m )");
print("".(((a mod m)+ (b mod m)) mod m)." =?= ".((a+b) mod m ));
76, 40, 116, 6, 5
"((a mod m)+ (b mod m)) mod m) =?= ((a+b) mod m )"
"4 =?= 4"
Mit zufälligen Zahlen immer wieder ansehen.
w:=random(1..1000):v:=random(1..1000):a:=w():b:=v():
print(a,b,a+b,a mod m, b mod m, (a mod m)+ (b mod m) mod m, " =?= ", (a+b) mod m )
769, 922, 1691, 6, 5, 4, " =?= ", 4
w:=random(1..1000):v:=random(1..1000):a:=w():b:=v():
print(a,b,a*b,a mod m, b mod m, ((a mod m)*(b mod m)) mod m, " =?= ", (a*b) mod m )
410, 656, 268960, 4, 5, 6, " =?= ", 6
w:=random(1..1000):v:=random(1..1000):vv:=random(1..100):a:=w():b:=v():m:=vv():
print(m,a,b,a*b,a mod m, b mod m, (a mod m)*(b mod m) mod m, " =?= ", (a*b) mod m)
61, 164, 458, 75112, 42, 31, 21, " =?= ", 21
Merke: Die Modulofunktion ist ein Homomorphismus,
eine strukturerhaltende Abbildung
Es ist also egal, an welcher Stellen der Ausrechnung man zu
der Resten übergeht.
#################################################################################
Erweitertes Arbeiten in Restklassenstrukturen
powermod(13,187,111); // 123 hoch 111 modulo 187
![]()
po:=13^111
![]()
modp(po,187)
![]()
powermod(13,111,187);
![]()
#######################################################################################
Bestimmung der Inversen
a:=541: m:=631: isprime(631)
![]()
Für in MuPAD funktioniert einfach
1/541 mod 631
![]()
Probe:
7*541 mod 631
![]()
Das aber muss geschickt programmiert sein.
Der Von-Hand-Algorithmus verwendet den erweiterten euklidischen Algorithmus,
dessen Ergebnis auch von MuPAD bescafft wird:
a:=541;m:=631; ggt:=igcdex(a,m);
![]()
![]()
![]()
s:=ggt[2]:t:=ggt[3]:gt:=ggt[1]:sa:=s*a:tm:=t*m:satm:=s*a+t*m;
![]()
Die Vielfachsummen-Darstellung (VSD, siehe auch Datei teiler-prim.mn) ist also
ggt(a,m)=s*a+t*m:
"ggt =".gt." = (".s.")*".a."+(".t.")*".m
![]()
"(".s.")*".a."+(".t.")*".m."=".sa."+(".tm.")=".satm." ist gleich ggt= ".gt
![]()
s ist invers zu a modulo m
bzw, falls s negativ, dann nimm s+m,
bzw kann man in MuPAD einfach die positive-Modulfunktion nehmen
s:=modp(s,m)
![]()
s*a mod m
![]()
#######################################################################################
Prime Restklassen-Gruppe Z*(a)
zstern:=proc(a)
local i,s;
begin
s:=[1];
for i from 2 to a-1 do
if gcd(a,i)=1 then
s:=append(s,i);
end_if;
end_for;
return(s);
end_proc:
zstern(12)
![]()
Definition einer eigenen Prozedur, verwendet im TI92/Voyage
eulerphi:=proc(a)
begin nops(zstern(a)) end_proc:
eulerphi(12)
![]()
[numlib::phi(a), eulerphi(a)] $ a=54..64
![]()
#######################################################################################
Ordnung der Elemente
a sei Element einer endlichen Gruppe.
Der minimale Exponent k, der a^k=1 erzeugt heißt "Ordnung von a"
a:=i:m:=18:zstern(m);eulerphi(m);
[a,numlib::order(a,m)] $a in zstern(m)
![]()
![]()
![]()
Satz: Die Ordnung jedes Gruppenelementes teilt die Gruppenordnung.
26^2 mod 27 //kleine Probe
![]()
Definition einer eigenen Prozedur, verwendet im TI92/Voyage
ordo:=proc(a,m)
local ordnung, pot;
begin
ordnung:=1: pot:=modp(a,m):
if gcd(a,m)>1 then return("".a." nicht teilerfremd zu ".m); end_if;
while pot>1 do
pot:=modp(pot*a,m): ordnung:=ordnung+1
end_while;
if pot=1 then return( ordnung); end_if;
end_proc:
ordo(2,27)
![]()
ordo(2,26)
![]()
m:=11:eulerphi(m);[a,numlib::order(a,m),ordo(a,m)] $a in zstern(m)
![]()
![]()
m:=12:zstern(m);ph:=eulerphi(m);
![]()
![]()
maltafel_m_stern:=array(1..ph,1..ph, [[i*j mod m $ i in zstern(m) ] $ j in zstern(m)]):
maltafel_m_stern

potenzTafelListe:=proc(liste,m,n)
local i,k;
begin
print(liste, " Potenzen modulo ".m);
matrix([i $ i=1..n]),
matrix([[k^i mod m $ k in liste] $ i=1..n]);
end_proc:
potenzTafelListe([3,7,9],10,8)
[3, 7, 9], " Potenzen modulo 10"
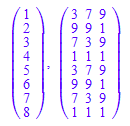
Man kann die zstern direkt einsetzen:
m:=15:
potenzTafelListe(zstern(m),m,nops(zstern(m)))
[1, 2, 4, 7, 8, 11, 13, 14], " Potenzen modulo 15"

#######################################################################################
Potenzieren im Modul (Entwicklung mit Erklärung auf eigener Seite)
powermod(17,4,120), modp(17^4,120)
![]()
Definition einer eigenen Prozedur, verwendet im TI92/Voyage
pmod:=proc(a,k,m)
local x_,h_,k_;
begin
k_:=k: x_:=1:pot:=a:
repeat
if modp(k_,2)=1 then
x_:= modp(x_*pot,m):
if k_=1 then return(x_):exit:end_if:
k_:=k_-1:
end_if:
k_:=k_/2:
pot:=modp(pot*pot,m):
until 3=1 end_repeat:
end_proc:
a:=5:m:=7:[pmod(a,k,m),powermod(a,k,m)] $k=1..12
![]()
a:=17:m:=120:[pmod(a,k,m),powermod(a,k,m)] $k=90..96
![]()