RSA-Verfahren und RSA-Signatur

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Dez 2010

0.1 Handlinghilfen

0.2 Inhalt

1 Schlüsselerzeugung
    1.1 Grundlage n und phi
    1.2 Schlüssel e und geheimes d
    1.3 Antons öffentlicher Schlüssel
2 Hilfsfunktionen !!!!!!! Aufkappen und auswerten!!!!!
    2.1 Text in Zahl
    2.2 Zahl in Text
3 Anwendungsphase Verschlüsselung
    3.1 Nachricht als Zahl erzeugen
    3.2 Nachricht verschlüsseln
4 Empfang und Entschlüsseln
    4.1 Errechnung der Nachrricht
    4.2 Text der Nachrricht
5 Signatur eines Textes
    5.1 Erzeugung der Signatur
    5.2 Prüfung der Signatur
    5.3 Angriff: Veränderung des Textes
    Merken das Angriffs

1 Schüsselerzeugung

Anton will sich ein Schlüsselpaar für das RSA-Verfahren herstellen

1.1 Grundlage n und phi

n wird grundsätzlich als Produkt aus zwei Primzahlen

(%i1) p:next_prime(floor(sqrt(random(1.0)*10^120)));
10^60;

(%i5) q:next_prime(floor(sqrt(random(1.0)*10^120)));
10^60;

(%i29) n:p*q; phi:(p-1)*(q-1);

1.2 Schlüssel e und geheimes d

e muss teilerfremd zu phi gewählt werden, damit es in Z*(phi) ein
Inverses d hat.

(%i33) /* $ unterdrückt die Ausgabe und # steht für ungleich */
e:2$ while gcd(e,phi)#1 do e:random(phi)$ e;

(%i36) d:gcdex(e,phi)[1]; if d<0 then d:d+phi$ d;

(%i39) mod(e*d,phi);

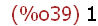
1.3 Antons öffentliches Schlüsselpaar

(%i17) e;n;

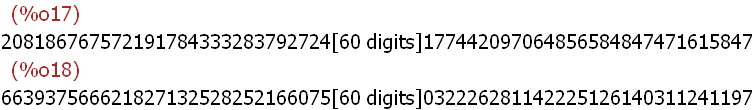
Dies stellt Anton öffentlich zur Verfügung, z.B. aus seiner
Internetseite.

2 Hilfsfunktionen

3 Anwendungphase, Verschlüsselung

Berta will Anton einen Text senden, den nur Anton lesen kann.
Sie liest im Internet (z.B.) Antons öffentliches Schlüsselpaar (e,n).

3.1 Nachricht als Zahl erzeugen

(%i42) m:txToZoo("Montag Treffen um 8 im Medley");

(%i43) /* soll 1 sein */ gcd(m,n);

3.2 Verschlüsseln

Nun potenziert sie m mit e modulo n

(%i44) c:power_mod(m,e,n);

Berta sendet c an Anton

4 Empfang und Verschlüsseln

Anton empfängt c.

4.1 Entschlüsseln der Nachricht

(%i45) mm:power_mod(c,d,n);

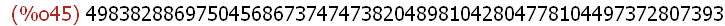
4.2 Zurückverwandeln in Text

(%i46) zooToTx(mm);

5 Digitale Signatur

Anton will einen offen lesbaren Text signieren. Es soll sich
jeder überzeugen können, dass der Text nicht verändert ist.
Auch bei der Signatur mit RSA wird modulo n potenziert, allerdings erst
mit d und dann mit c.

5.1 Erzeugung der Signatur

Antond Text:

(%i47) M:txToZoo("Vertraut Emil nicht");

Signatur

(%i48) sig:power_mod(M,d,n);

Normalerweise wird die Zahl M erst noch einer "Hash-Funktion" übergeben,
die weniger Datenplatz braucht und es wird h(M) signiert.

5.2 Prüfung der Signatur

Berta will sich überzeugen, dass der auf Antons Site lesbare Text
von niemandem manipuliert wurde. Sie verwendet dazu das öffenliche
RSA-Schlüsselpaar (e,n).

(%i49) MM:power_mod(sig,e,n);

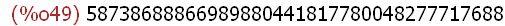
Falls keine Hashfunktion werwendet wurde, kann sie diese Zahl in Text
umwandeln und lesen. Es muss derselbe Text sein, den sie bei Anton
gelesen hatte.

(%i50) zooToTx(MM);

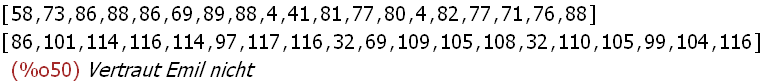
Hat Anton einen Hashwert signiert, nimmt Berta anstelle des Textes auch
den Hashwert h(M) und vergleicht mit MM.
Anton hat in diesem Fall das Hashverfahren angegeben.

5.3 Veränderng des Textes

Mister X macht aus Antons Text etwas anderes

(%i51) MX:txToZoo("Vertraut Emil");

Wenn er die Signatur so lässt, merkt Berta sofort, dass das ein anderer Text
ist. Aber die kleinste Veränderung der Signatur ist auch merkbar:

(%i52) sigX:sig+1;

Berta nimmt erstmal diese Signatur als richtig an und rechnet

(%i53) MMX:power_mod(sigX,e,n);

(%i54) zooToTx(MMX);

Das ergibt nichts Sinnvolles!
Bei Hash-Verwendung würden h(M) und MMX nicht übereinstimmen.